Question

A motor cyclist is riding North in still air at 36 km/h. The wind starts blowing Westward with a velocity 18 km/h. The direction of apparent velocity is:
A. ${{\tan }^{-1}}(\dfrac{1}{2})$ West of North
B. ${{\tan }^{-1}}(\dfrac{1}{2})$ North of West
C. ${{\tan }^{-1}}(\dfrac{1}{2})$ East of North
D. ${{\tan }^{-1}}(\dfrac{1}{2})$ North of East

Answer 1

Hint: The discussion of relative motion in one or more dimensions is where the idea of reference frames was originally introduced. When we state that an object has a given velocity, we mean that this velocity is relative to the so-called reference frame. In daily life, the ground or the earth is assumed to be the reference frame when measuring an object's velocity.

Complete step by step solution:
Two-dimensional relative motion will be able to solve this problem. If you need to determine how fast A is moving relative to B, assume that B is at rest and provide A B's speed in the opposite direction.

Let's take into consideration two objects A and B that are travelling at speeds $V_a$ and $V_b$, respectively, according to some common frame of reference, such as the ground or the earth. Assuming B is at rest, we must determine the velocity of A with respect to B before applying the velocity of B to A in the opposite direction.
${{V}_{ab}}={{v}_{a}}-{{v}_{b}}$
Similar to this, to get the velocity of object B relative to object A, suppose that A is at rest and apply the opposite direction of A's velocity to B's velocity.
${{V}_{ba}}={{v}_{b}}-{{v}_{a}}$

Given: Velocity of cyclist in North $({{V}_{c}})$= 36Km/h and Velocity of wind in west $({{V}_{w}})$= 18Km/h

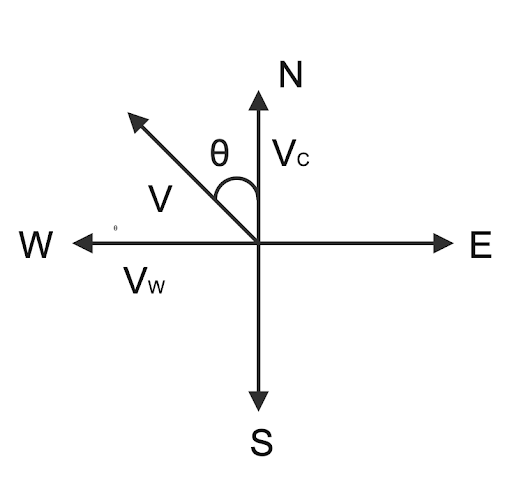
Direction of motion = tanθ
∴ tanθ = $\dfrac{{{V}_{w}}}{{{V}_{C}}}$=$\dfrac{18}{36}$
tanθ = $\dfrac{18}{36}$
∴ θ= ${{\tan }^{-1}}(\dfrac{1}{2})$
From fig. direction of apparent velocity is,
θ= ${{\tan }^{-1}}(\dfrac{1}{2})$ in West of North

Hence, option A is correct.

Note: There is a chance that students may get confused between the concepts of velocity and relative velocity. Velocity is measured with respect to a reference point which is relative to a different point whereas relative velocity is measured with reference to a frame where an object is either moving or at rest with respect to the absolute frame. When viewed from a fixed point of observation, the item is said to be moving absolutely (there is no change in the position of an observer). Relative motion refers to the movement of an object when there is no fixed point of view (the position of the observer changes with respect to time).