Question

: A metal crystallises in face centred cubic structure. If the edge of its unit cell is ‘a’, the closest approach between two atoms in metallic crystal will be:
(A) ${\rm{2}}\sqrt {{\rm{2a}}} $
(B) $\sqrt {{\rm{2a}}} $
(C) $\dfrac{{\rm{a}}}{{\sqrt {\rm{2}} }}$
(D) ${\rm{2a}}$

Answer 1

Hint: We know that, in the face centred cubic structure the number of atoms present in it is four. Generally, the one atom is present or exists in the center and three atoms present at the corner of the FCC structure. The FCC is one of the abbreviations used for representing the face centred cubic.

Complete step-by-step solution:As we all know, for FCC crystal or face cubic structure, the closet method between two atoms in metallic crystal will be equal to the half the length of the face diagonal. It generally be represented as $\dfrac{1}{2} \times {\rm{length}}\;{\rm{of}}\;{\rm{diagonal}}......\left( 1 \right)$.
But the length of the face diagonal of the face cubic structure is $\sqrt {{\rm{2a}}} ......\left( 2 \right)$.
Where, ‘a’ is the edge of the unit cell.
So, equating the equations (1) and (2), for getting the closet value between the atoms in a metallic crystal as shown below.
$\dfrac{1}{2} \times \sqrt {{\rm{2a}}} = \dfrac{{\rm{a}}}{{\sqrt {\rm{2}} }}$
Thus, for “a metal crystallises in face centred cubic structure. If the edge of its unit cell is ‘a’, the closet approach between two atoms in metallic crystal” will be $\dfrac{{\rm{a}}}{{\sqrt {\rm{2}} }}$ as shown in the image below:

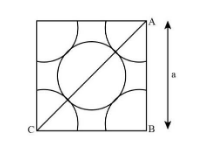
Hence, the correct option for this question is C that is $\dfrac{{\rm{a}}}{{\sqrt {\rm{2}} }}$.

Note:Usually, the crystals are divided into seven main types. Generally, it is divided on the basis of the number of atoms present in the crystals at the corner and at the center and the arrangement of atoms or ions in the crystal. The process is normally termed as crystallography.