
A liquid if filled into a semi elliptical cross section with a semi major axis and b as a semi minor axis. The ratio of surface tension forces on the curved part and the plane part of tube in vertical position will be:
A) $\dfrac{{\pi \left( {a + b} \right)}}{{4b}}$
B) $\dfrac{{2\pi A}}{b}$
C) $\dfrac{{\pi A}}{{4b}}$
D) $\dfrac{{\pi \left( {a - b} \right)}}{{4b}}$
Answer
233.1k+ views
Hint: The surface or curved tension force f is equal to the product of the tension along it and the perimeter of that part. We will find both the forces along the curved and flat surface and then their ratio will be our solution.
Complete step by step answer:
Step 1:
We are given:
A liquid if filled into a semi elliptical cross section with a as semi major axis and b as semi minor axis.
And we need to find the ratio of surface tension forces on the curved part and the plane part of tube in vertical position.
Now, coming to the solution:
To clearly understand the language of question and way to solution let us consider a diagram below;
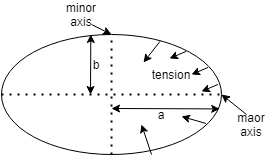
We have an elliptical tube having a as a semi major axis and b as a semi minor axis of it.
In semi-elliptical we can have two cases: either along semi major axis or along semi minor axis
Let us take along the minor axis as shown in the figure.
Step 2:
In figure the arrows on the semi minor axis are depicting the surface tension force.
Then force on the minor axis will be${f_M}$ =the product of tension and length of the minor axis
This implies${f_M}$ =T × 2b
Force on the curved part will be ${f_C}$ =the product of tension and half the perimeter of semi ellipse which is $\dfrac{{\pi \left( {a + b} \right)}}{2}$
This implies ${f_C}$ =T × $\dfrac{{\pi \left( {a + b} \right)}}{2}$
Now, the ratio of surface tension forces on the curved part and the plane part of tube in vertical position will be $\dfrac{{{f_C}}}{{{f_M}}}$ =$\dfrac{{\pi \left( {a + b} \right)}}{2} \times \dfrac{1}{{2b}}$
On further solving this will ultimately equal to $\dfrac{{{f_C}}}{{{f_M}}}$ =$\dfrac{{\pi \left( {a + b} \right)}}{{4b}}$
This means the ratio of surface tension forces on the curved part and the plane part of tube in vertical position will be$\dfrac{{\pi \left( {a + b} \right)}}{{4b}}$
Hence option A is correct.
Note: Every time while doing such a question it is important to make diagrams wherever it is possible because diagrams give us a clear vision of finding the solution like in this question we have found out the ration by taking the minor axis and the curve along it.
Complete step by step answer:
Step 1:
We are given:
A liquid if filled into a semi elliptical cross section with a as semi major axis and b as semi minor axis.
And we need to find the ratio of surface tension forces on the curved part and the plane part of tube in vertical position.
Now, coming to the solution:
To clearly understand the language of question and way to solution let us consider a diagram below;

We have an elliptical tube having a as a semi major axis and b as a semi minor axis of it.
In semi-elliptical we can have two cases: either along semi major axis or along semi minor axis
Let us take along the minor axis as shown in the figure.
Step 2:
In figure the arrows on the semi minor axis are depicting the surface tension force.
Then force on the minor axis will be${f_M}$ =the product of tension and length of the minor axis
This implies${f_M}$ =T × 2b
Force on the curved part will be ${f_C}$ =the product of tension and half the perimeter of semi ellipse which is $\dfrac{{\pi \left( {a + b} \right)}}{2}$
This implies ${f_C}$ =T × $\dfrac{{\pi \left( {a + b} \right)}}{2}$
Now, the ratio of surface tension forces on the curved part and the plane part of tube in vertical position will be $\dfrac{{{f_C}}}{{{f_M}}}$ =$\dfrac{{\pi \left( {a + b} \right)}}{2} \times \dfrac{1}{{2b}}$
On further solving this will ultimately equal to $\dfrac{{{f_C}}}{{{f_M}}}$ =$\dfrac{{\pi \left( {a + b} \right)}}{{4b}}$
This means the ratio of surface tension forces on the curved part and the plane part of tube in vertical position will be$\dfrac{{\pi \left( {a + b} \right)}}{{4b}}$
Hence option A is correct.
Note: Every time while doing such a question it is important to make diagrams wherever it is possible because diagrams give us a clear vision of finding the solution like in this question we have found out the ration by taking the minor axis and the curve along it.
Recently Updated Pages
Dimensions of Charge: Dimensional Formula, Derivation, SI Units & Examples

How to Calculate Moment of Inertia: Step-by-Step Guide & Formulas

Circuit Switching vs Packet Switching: Key Differences Explained

Dimensions of Pressure in Physics: Formula, Derivation & SI Unit

JEE General Topics in Chemistry Important Concepts and Tips

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




