Question

A galvanometer of resistance $100\Omega $ gives full scale deflection with $5mA$current. To convert it into a $5$ volt range voltmeter, the value of resistance connected in series is:
(A) $900\Omega $
(B) $9999\Omega $
(C) $10000\Omega $
(D) $1M\Omega $

Answer 1

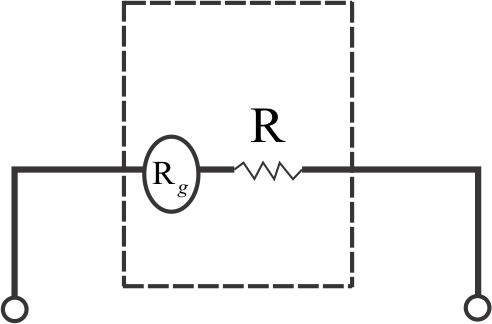
Hint: In order to convert a galvanometer into a voltmeter, a high resistance R is connected in series. Let V be the voltage drop across the circuit. Firstly, we will calculate the ${R_{eq}}$ i.e., the equivalent resistance of the circuit, since the range as well as full scale deflection current is given hence using Ohm’s law, we will calculate the required resistance.

Complete step by step answer
Given:
$V = 5V$
full scale deflection current $ = I = 5mA$
and, ${R_g} = 100\Omega $
Firstly, we will find ${R_{eq}}$
Since both the resistances are in series therefore, we have
$
  {R_{eq}} = R + {R_g} \\
  {R_{eq}} = 100 + R......(1) \\
 $
Given the range of voltmeter and the full-scale deflection current.
Hence, from Ohm’s law, we have
$
  V = I{R_{eq}}......(2) \\
    \\
$
Using above values in equation (1) and (2), we get
$5 = 5mA(R + 100)......(3)$
On solving above equation, we get
$
  5 = 5 \times {10^{ - 3}}(R + 100) \\
  1000 = R + 100 \\
  R = 900\Omega \\
 $
Hence the required resistance connected in series is $R = 900\Omega $ .

Option (A) is correct.

Note When the voltmeter is used in a circuit, its resistance ${R_{eq}}$ is connected in parallel to some element of the circuit. This changes the overall current in the circuit and hence, the potential difference to be measured is also changed. To minimize the error due to this, the equivalent resistance ${R_{eq}}$ should be large. (when a large resistance is connected in parallel to a small resistance, the equivalent resistance is only slightly less than the smaller one.) That is why, a large resistance R is added in series with the coil of a voltmeter.