Question

A cook uses the fire tongs of length 28 cm, to lift a piece of burning coal of mass 250 g. If he applies the effort at a distance of 7 cm from the fulcrum, find the effort in the S.I unit.

Answer 1

Hint:-This given problem can be solved by taking the consideration of the phenomena of lever. A lever can be defined as a simple machine which consists of a beam or rigid rod rotated at a fixed hinge, or fulcrum. A lever is a rigid body that can rotate on a point itself.

Complete step-by-step solution:
Step 1:

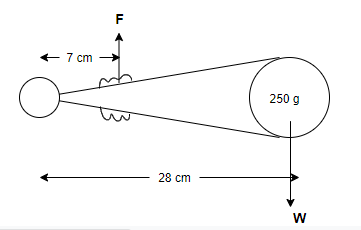
It can be seen from the above figure that two forces are acting on the fire tong and these two forces are acting in opposite directions, i.e., clockwise and counterclockwise.
If these two forces are unequal forces when acting in opposite directions the equilibrium can be established about a point if the product of the magnitude of one force and its effort arm, or lever arm (also known as the distance of its point of application from the fulcrum), is equal to the product of the other force and its effort arm.
We also know that the product of a force by its effort arm is known as a moment of the given force. So, it is also known as the principle of moments of states in which equilibrium is established i.e., when the sum of the moments of the forces acting in the clockwise direction is equal to the sum of the moments of the forces acting in counter clockwise direction.
Step 2: So, from above statements we can solve this problem –
Length of fire tong, (say) \[\mathop L\nolimits_2 = 28\]cm
Length at which effort is applied from the fulcrum, (say) \[\mathop L\nolimits_1 = 7\]cm
So, from the condition of lever mechanism, we know that – moment of effort will be equal to moment of applied force i.e.,
Moment of effort = moment of applied force (load)
\[\mathop {F \times L}\nolimits_1 = W \times \mathop L\nolimits_2 \] (1)
Keeping the values, we will get –
\[\Rightarrow F \times 7 = W \times 28\] where \[W = mg\] and \[g = 10\]m/s2
So, \[W = \dfrac{{250}}{{1000}} \times 10\]
On further solving the above equation –
\[\Rightarrow F \times 7 = \dfrac{{250}}{{1000}} \times 10 \times 28\]
\[\Rightarrow F = \dfrac{1}{4} \times 10 \times 4\]
\[\Rightarrow F = 10\]N.

So, the effort in S.I. unit is 10N.

Note:- Levers are used to exert a large force over a small distance at one end by exerting only a small force (effort) over a greater distance at the other.
If equal and opposite forces are applied to a uniform lever at equal distances from the fulcrum, then the moments will counteract each other and establish a state of equilibrium, or balance, in the lever.