Question

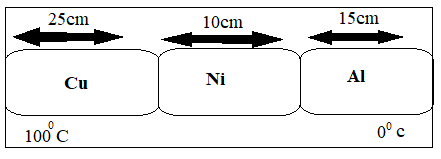
A composite metal bar of the uniform section is made up of 25 cm of copper, 10 cm of nickel, and 15 cm of aluminium. Each part is in perfect thermal contact with the adjoining part. The copper end of the composite rod is maintained at $100{}^\circ C$ and the aluminium end at $0{}^\circ C$. The whole rod is covered with a belt so that no heat loss occurs at the sides. If ${{K}_{Cu}}=2{{K}_{Al}}$​ and ${{K}_{Al}}=3{{K}_{Ni}}$, then what will be the temperatures of Cu-Ni and Ni-Al junction respectively.

A. $23.33{}^\circ C$ and $78.8{}^\circ C$
B. $83.33{}^\circ C$ and $20{}^\circ C$
C. $50{}^\circ C$ and $30{}^\circ C$
D. $30{}^\circ C$ and $50{}^\circ C$

Answer 1

Hint: Here as in the question three metals of different thermal conductivity are joined together. The temperature at the two ends and relation connecting thermal conductivities of these metals are already given. We have to find the temperature of each junction. We use the equation of rate of flow of heat to find the temperature at each junction.

Formula used:
Rate of heat flow is:
\[\dfrac{dQ}{dt}=kA\dfrac{\left( {{\theta }_{1}}-{{\theta }_{2}} \right)}{L}\]
Where Q is the heat flowing, k is the thermal conductivity of the material, A is the area and L be the length of the conductor and \[\left( {{\theta }_{1}}-{{\theta }_{2}} \right)\] be the difference in temperature.
And since all metal bars are connected in series,
\[{{\left( \dfrac{Q}{t} \right)}_{combination}}={{\left( \dfrac{Q}{t} \right)}_{Cu}}={{\left( \dfrac{Q}{t} \right)}_{Al}}={{\left( \dfrac{Q}{t} \right)}_{Ni}}\]
We can also write in terms of thermal conductivity as:
$\dfrac{3}{{{K}_{eq}}}=\dfrac{1}{{{K}_{eq}}}+\dfrac{1}{{{K}_{Al}}}+\dfrac{1}{{{K}_{Ni}}}$

Complete step by step solution:
There is a composite metallic bar made up of copper, aluminium and nickel. It has a uniform cross section.
Length of copper= 25 cm
Length of aluminium= 15 cm
Length of nickel= 10 cm
The copper end of the composite rod is maintained at $100{}^\circ C$ and the aluminium end at $0{}^\circ C$. The whole rod is covered with a belt so that no heat loss occurs at the sides.

Let thermal conductivity of nickel is taken as K. Then relation connecting thermal conductivities of different metals is:
${{K}_{Cu}}=6K$and ${{K}_{Al}}=3K$
Then equation connecting thermal conductivity of different metals connected in series become:
$\dfrac{3}{{{K}_{eq}}}=\dfrac{1}{{{K}_{eq}}}+\dfrac{1}{{{K}_{Al}}}+\dfrac{1}{{{K}_{Ni}}}=\dfrac{9}{6K} \\ $
That is equivalent thermal conductivity is equal to:
${{K}_{eq}}=2K$

Let \[{{\theta }_{1}}\] be the temperature at copper-nickel junction and \[{{\theta }_{2}}\]be the temperature at nickel aluminium junction. Hence from the equation:
\[{{\left( \dfrac{Q}{t} \right)}_{combination}}={{\left( \dfrac{Q}{t} \right)}_{Cu}}={{\left( \dfrac{Q}{t} \right)}_{Al}}={{\left( \dfrac{Q}{t} \right)}_{Ni}} \\ \]
Only taking first part of the equation,
That is, taking \[{{\left( \dfrac{Q}{t} \right)}_{combination}}={{\left( \dfrac{Q}{t} \right)}_{Cu}}\] we get:
\[{{K}_{eq}}A\left( \dfrac{\left( 100-0 \right)}{25+10+15} \right)={{K}_{Cu}}A\dfrac{\left( 100-{{\theta }_{1}} \right)}{25} \]

On putting values of thermal conductivity, we get temperature at the copper and nickel junction as:
${{\theta }_{1}}=83.33{}^\circ C$
Similarly using the relation \[{{\left( \dfrac{Q}{t} \right)}_{combination}}={{\left( \dfrac{Q}{t} \right)}_{Al}}\] we get temperature at nickel and aluminium junction as:
$\therefore {{\theta }_{2}}=20{}^\circ C$

Therefore, the answer is option B.

Note: In order to find the temperature at the junction we use the relations connecting the metals at both ends only; we don't use the middle one since we deal with the rate of flow of heat.