Question

A cell of e.m.f. \[1.5\,V\] and internal resistance \[1.0\Omega \] is connected to two resistors of \[4.0\Omega \] and \[20.0\Omega \] in a series. Draw the circuit diagram and calculate the:
(i) Current in the circuit,
(ii) Potential difference across the \[4.0\Omega \] resistor,
(iii) Voltage drop when the current is flowing,
(iv) Potential difference across the cell.

Answer 1

Hint:The potential difference in a circuit is given by the Ohm’s law. The potential drop across a resistor is given by the product of the current through the circuit and the resistance

Formula used:
The voltage across a cell of certain e.m.f is given by,
\[V = E - Ir\]
where, \[E\] is the e.m.f of the cell \[I\] is the current through the circuit and \[r\] is the internal resistance of the cell.
The voltage drop across any component of resistance \[R\] is given by,
\[V = IR\]
where \[I\] is the current through the resistor and \[R\] is the value of the resistance.

Complete step by step answer:
Here we have a cell of e.m.f of \[E = 1.5V\] having an internal resistance of \[r = 1\Omega \] is connected with resistance \[4.0\Omega \] and \[20.0\Omega \] in series. So, the circuit diagram is given as follows.

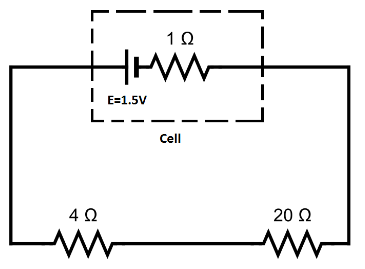
(i) Now, we have to find the net current through the circuit. The voltage drop across a cell is given by,
\[V = E - Ir\]
Now, voltage drop across the cell is the voltage drop across the resistances. So,
\[IR = E - Ir\]
Or, current, \[I = \dfrac{E}{{R + r}}\]
Now, total resistance of the circuit is, \[4 + 20 + 1 = 25\Omega \]
e.m.f of the cell is, \[E = 1.5V\]
So, the current flowing through the circuit is, \[I = \dfrac{{1.5}}{{25}} = 0.06A\]

(ii) So, the potential difference across the \[4.0\Omega \] is equal to,
\[V = 4 \times 0.06 = 0.24\,V\]
So, the potential difference is \[0.24\,V\].

(iii) voltage drop across the cell is \[V = Ir\]
Putting the values we have, \[0.06 \times 1 = 0.06\,V\]
So, voltage drop of the cell when the current is flowing is \[0.06\,V\].

(iv) The potential difference across the cell is the same as the potential differences of the resistances. So, The potential difference across the cell,
\[V = IR\]
\[\Rightarrow 0.06 \times (20 + 4) = 1.44\,V\]
So, the potential difference across the cell is \[1.44\,V\].

Note: The e.m.f of any cell does not depend on any exterior property of the circuit. It purely depends on the composition of the cell. The e.m.f of any practical cell cannot be fully utilized due to the presence of internal resistance of the cell. It decreases the potential drop across the cell.