Question

A capacitor of emf E is charged by a cell and the charging battery is then removed. If a similar capacitor is now inserted in the circuit in parallel with the previous capacitor, then calculate the potential difference across the new capacitor is :
A. $2E$
B. $E$
C. $\dfrac{E}{2}$
D. $ZERO$

Answer 1

Hint:-The best approach to solve these questions is to check the connections of the battery, if the battery is removed then charge is constant and if battery is connected then Potential difference will be constant. Now we have direct formulas for calculating net connection of capacitors in series and parallel
Two capacitor case:
For series ${C_{net}} = {C_1} + {C_2}$
For parallel $\dfrac{1}{{{C_{net}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}$

Complete step-by-step solution:-
According to the question given, we have to calculate the potential difference across new capacitor
Now when the new capacitor added the charge started flowing across the new capacitor just to make the potential difference equal on both the sides.
So, let the two capacitors be ${C_1}$ and ${C_2}$
As the battery is disconnected so the total charge is constant that is ${Q_t} = CE$ where Q is the total charge, E is the potential from the battery and C is the capacitance which is net after the addition of new capacitor

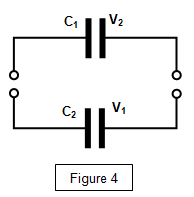
When a identical capacitor is add in parallel so the total capacitance is,
${C_{net}} = {C_1} + {C_2} = C + C = 2C$
Now the common potential
$ = \dfrac{{{\text{total charge}}}}{{{\text{total capacity}}}} = \dfrac{{CE}}{{2C}}$
$ = \dfrac{E}{2}$
So, the potential difference across new capacitor is $\dfrac{E}{2}$

Hence the correct option is (C )

Note:- Point to be noted, In the capacitors charge transfer takes place in such a way that the potential at both the capacitors become equal. In case if the battery remains connected then the transfer of potential takes place so that charge in both the capacitors become equal.