Question

A breeder crossed a purebred tall pea plant having white flowers to a pure-bred short pea plant with blue flowers. He obtained $202\,{F_1}$ progeny and found that they are tall and have white flowers. Upon selfing these plants, he obtained a progeny of $2160$ plants approximately, how many of these are likely to be short and blue flowers?
(A) $1215$
(B) $405$
(C) $540$
(D) $135$

Answer 1

Hint: The dihybrid cross is defined as the cross between the two different genes of the same species. It expresses the dominant and the recessive genes. From the dihybrid test cross ratio, find the number of plants of particular traits asked by using the formula.

Complete answer:
In a dihybrid cross
$n = r \times \left( {\dfrac{T}{R}} \right)$
Where $n$ is the number of plants exhibiting the particular traits, $r$ is the ratio of the particular trait, $T$ is the total number of plants obtained and $R$ is the sum of the ratio of all the traits.

Complete step by step solution:
From the given data in the question,
The number of progenies obtained in the ${F_1}$ generation= $202$
The number of progenies obtained in the ${F_2}$ generation= $2160$
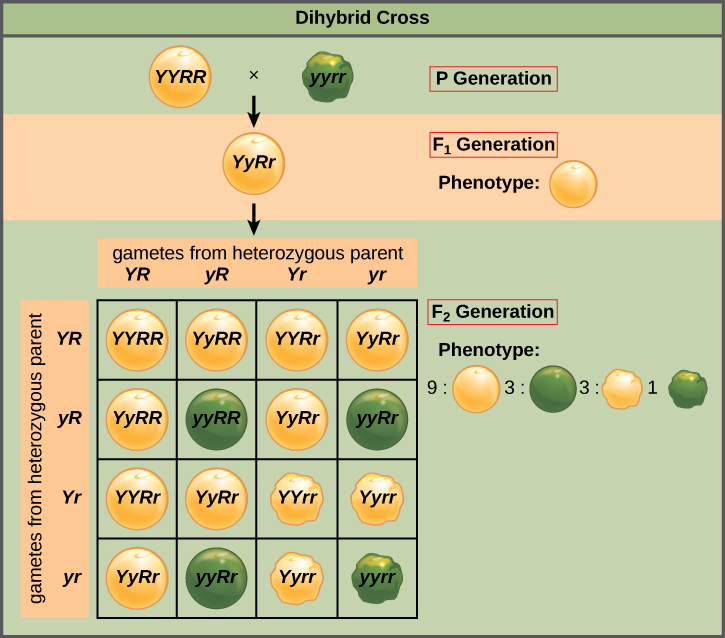
In a dihybrid cross the ${F_2}$ generation obtained is in the ratio of $9:3:3:1$.

This means that the $9x$ species is the number of the expressed dominant gene. That is, it denotes the number of the tall flowers with the white flowers. Then the $3x$denotes the both the dominant and the recessive genes expressed in the ${F_2}$ generation. That is, it may be tall plants with the blue flowers or it may be the short plants with the white plants. Then, $1x$ denotes the expression of the recessive gene in the ${F_2}$ generation. It expresses the short plants with the blue flowers.
Hence the number of the short plants with the blue flower in the ${F_2}$ generation is $1x$.
Applying the dihybrid cross formula.
$n = r \times \left( {\dfrac{T}{R}} \right)$
$n = 1 \times \left( {\dfrac{{2160}}{{9 + 3 + 3 + 1}}} \right)$
$n = \dfrac{{2160}}{{16}}$
$n = 135\,plants$

Hence the correct answer is OPTION(D)

Note: It is to be noted that, in the ${F_1}$ generation plants, the heterogeneous gene is expressed. In the ${F_2}$ generation, the gene with the dominant, recessive and the combination of the both dominant and the recessive characters is expressed.