Question

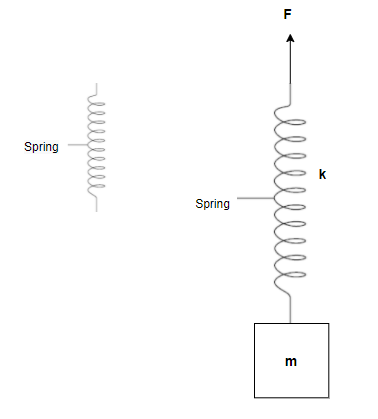
A block of mass m is connected to a spring (spring constant k). Initially the block is at rest and the spring is in its natural length. Now the system is released in gravitational field and a variable force F is applied on the upper end of the spring such that the downward acceleration of the block is given as a=g−αt, where t is time elapses and α=1m/s3, the velocity of the point of application of the force is

(A) \[\dfrac{m}{k} - gt + \dfrac{{\mathop t\nolimits^2 }}{2}\]
(B) \[\dfrac{m}{k} + gt + \dfrac{{\mathop t\nolimits^2 }}{2}\]
(C) \[\dfrac{m}{k} - gt - \dfrac{{\mathop t\nolimits^2 }}{2}\]
(D) \[\dfrac{m}{k} - gt - \mathop t\nolimits^2 \]

Answer 1

Hint:-The given problem can be solved by taking the consideration of phenomena of a spring and a mass attached to it. When a mass is attached to it then there are forces working on the mass and this problem can be solved by taking the consideration of these masses.

Complete step-by-step solution:
Step 1: As it is given in the problem the force that is working on the upper end of the spring is variable force and the acceleration by which the block of mass m is moving downwards is \[a = g - \alpha t\], where t is the time of elapse and \[\alpha = 1\]m/s2.
Let the original length of the spring at rest is \[\mathop l\nolimits_0 \] and after the block of mass m is attached to the spring then it’s length is \[l\].
So, the elongation in length of the spring (let say \[x\]) then \[x = l - \mathop l\nolimits_0 \] at a time t.

This \[x\] can be defined as the total elongation due to the body, m (say) \[\mathop x\nolimits_b \], and due to force, F (say) \[\mathop x\nolimits_f \].
So, \[x = \mathop x\nolimits_b + \mathop x\nolimits_f \] …………………….. (1)
Now considering the body, the force equation will be
\[mg - kx = ma\]
Where \[mg = \]weight, \[kx = \]spring force, and \[ma = \]force due to acceleration on mass
And \[a = g - \alpha t\] …………………………. (2)
On solving the equation (1) and keeping the value from equation (2), we will get –
\[mg - kx = m\left( {g - \alpha t} \right)\] on solving this equation
\[\Rightarrow - kx = - m\alpha t\]
\[\Rightarrow x = \dfrac{{m\alpha t}}{k}\] ……………. (3)
Step 2: To get the velocity, we can differentiate the equation (3), we will get –
\[\Rightarrow \dfrac{{dx}}{{dt}} = \dfrac{{m\alpha }}{k}\dfrac{{dt}}{{dt}}\]
\[\Rightarrow \dfrac{{dx}}{{dt}} = \dfrac{{m\alpha }}{k}\]
But we know that from equation (1), we will get –
\[\Rightarrow \dfrac{{d\left( {\mathop x\nolimits_b + \mathop x\nolimits_f } \right)}}{{dt}} = \dfrac{{m\alpha }}{k}\]
\[\Rightarrow \mathop v\nolimits_b + \mathop v\nolimits_f = \dfrac{{m\alpha }}{k}\] ……………….(4)
Where \[\mathop v\nolimits_b \] and \[\mathop v\nolimits_f \] are the velocities of block of mass m and the point of application of force respectively.
Step 3: But we also know that –
\[a = g - \alpha t\]
And \[\dfrac{{d\mathop v\nolimits_b }}{{dt}} = g - \alpha t\] on further solving this equation
\[\Rightarrow d\mathop v\nolimits_b = (g - \alpha t)dt\]
On, integrating the above equation –
\[\Rightarrow \int {d\mathop v\nolimits_b = \int {(g - \alpha t)dt} } \] on further solving this equation –
\[\Rightarrow \mathop v\nolimits_b = gt - \dfrac{{\alpha \mathop t\nolimits^2 }}{2}\] ……………………….(5)
So from equation (4) and (5)
\[\Rightarrow gt - \dfrac{{\alpha \mathop t\nolimits^2 }}{2} + \mathop v\nolimits_f = \dfrac{{m\alpha }}{k}\]
\[\Rightarrow \mathop v\nolimits_f = \dfrac{{m\alpha }}{k} - gt + \dfrac{{\alpha \mathop t\nolimits^2 }}{2}\] where \[\alpha = 1\]m/s2
So, \[\Rightarrow \mathop v\nolimits_f = \dfrac{m}{k} - gt + \dfrac{{\mathop t\nolimits^2 }}{2}\]

So, the correct option is (A).

Note:- When the spring is compressed or elongated, it tends to recover its original length, on account of elasticity. The force trying to bring the spring back to its original configuration is called restoring force or spring force.