Question

A bag contains 3 red and 3 green balls and a person draws out 3 at random. He then drops 3 blue balls into the bag and again draws out 3 at random. The chance that the 3 later balls are all of different colour is.

Answer 1

Hint:Probability of event to happen \[P\{ E\} \]
\[ = \dfrac{{Number\,of\,favourable\,outcome}}{{Total\,Number\,of\,outcomes}}\]
In this question we will be creating two different cases as the balls were drawn two times. In the first case the total number of balls in the bag were 6 out of which 3 are red and 3 are green. In the second case the number of balls in the bag are 6 as well out of which 3 are blue.
In the second case we don’t know anything about the colour of the other 3 balls those were drawn out from the bag.

Complete step-by- step solution:

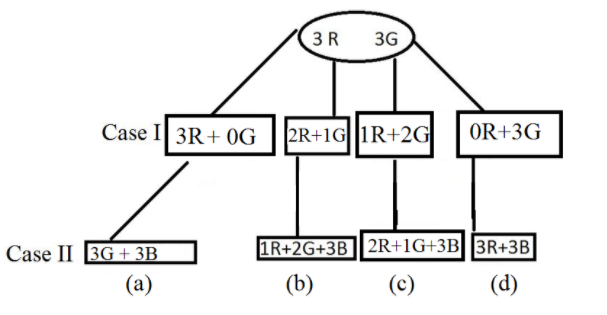
Given the data according to the question and its probability cases
Case I:
There are 3 red and 3 green balls in a bag and a person draws 3 balls.
The possibilities are the following:
3 red, 0 green
2 red, 1 green
1 red, 2 green
0 red, 3 green

Case II:
 As 3 blue balls have been added to the bag then the possibilities of the balls that are in the bag according to above cases are:
1) If 3 red, 0 green balls were drawn from the bag then there will be 0 red, 3 green and 3 blue balls in the bag.
2) 2 red, 1 green ball were drawn from the bag then there will be 1 red, 2 green and 3 blue balls in the bag.
3) 1 red, 2 green balls were drawn from the bag then there will be 2 red, 1 green and 3 blue balls in the bag.
4) 0 red, 3 green balls were drawn from the bag then there will be 3 red, 0 green and 3 blue balls in the bag.
We need to find the probability of three balls being different colours hence it rules out (a) and (d) cases.
Now, probability of withdrawing 2R, 1G is: \[ = \dfrac{{{}^3{C_1} \times {}^3{C_1}}}{{{}^6{C_3}}}\]
Probability of withdrawing 1R, 1G and 1B ball is: \[\dfrac{{{}^2{C_1} \times {}^1{C_1} \times {}^3{C_1}}}{{{}^6{C_3}}}\]
Hence, the probability of both cases is:
\[ = \dfrac{{{}^3{C_1} \times {}^3{C_1}}}{{{}^6{C_3}}} \times \dfrac{{{}^2{C_1} \times {}^1{C_1} \times {}^3{C_1}}}{{{}^6{C_3}}}\]
\[ = \dfrac{{\dfrac{{3!}}{{2!1!}} \times \dfrac{{3!}}{{2!1!}}}}{{\dfrac{{6!}}{{3!3!}}}} \times \dfrac{{\dfrac{{2!}}{{1!1!}} \times 1 \times \dfrac{{3!}}{{2!1!}}}}{{\dfrac{{6!}}{{3!3!}}}}\]
\[ = \dfrac{{\dfrac{{3 \times \not 2!}}{{\not 2!}} \times \dfrac{{3 \times \not 2!}}{{\not 2!}}}}{{\dfrac{{\not 6 \times 5 \times 4 \times \not 3!}}{{3! \times 3\not ! \times \not 2 \times 1}}}} \times \dfrac{{2! \times \dfrac{{3 \times 2!}}{{\not 2!}}}}{{\dfrac{{\not 6 \times 5 \times 4 \times \not 3!}}{{\not 3! \times 3! \times 2 \times 1}}}}\]
\[ = \dfrac{9}{{20}} \times \dfrac{6}{{20}} = \dfrac{{27}}{{200}}\,\,\,\,\,\,\,.......(1)\]
Now case II as the number of balls are same just colours are different, we have:
\[ = \dfrac{{{}^3{C_2} \times {}^3{C_1}}}{{{}^6{C_3}}} \times \dfrac{{{}^1{C_1} \times {}^2{C_1} \times {}^3{C_1}}}{{{}^6{C_3}}}\]
\[ = \dfrac{{\dfrac{{3!}}{{2!1!}} \times \dfrac{{3!}}{{2!1!}}}}{{\dfrac{{6!}}{{3!3!}}}} \times \dfrac{{\dfrac{{2!}}{{1!1!}} \times 1 \times \dfrac{{3!}}{{2!1!}}}}{{\dfrac{{6!}}{{3!3!}}}}\]
\[ = \dfrac{{\dfrac{{3 \times \not 2!}}{{\not 2!}} \times \dfrac{{3 \times \not 2!}}{{\not 2!}}}}{{\dfrac{{\not 6 \times 5 \times 4 \times \not 3!}}{{3! \times 3\not ! \times \not 2 \times 1}}}} \times \dfrac{{2! \times \dfrac{{3 \times 2!}}{{\not 2!}}}}{{\dfrac{{\not 6 \times 5 \times 4 \times \not 3!}}{{\not 3! \times 3! \times 2 \times 1}}}}\]
\[ = \dfrac{9}{{20}} \times \dfrac{6}{{20}} = \dfrac{{27}}{{200}}\,\,\,\,\,\,\,.......(2)\]
\[ = \dfrac{{27}}{{200}}.....(2)\]
Probability of 3 later balls being all of different colours \[ = \dfrac{{27}}{{200}} + \dfrac{{27}}{{200}}\](from \[e{q^n}\] 1 & 2)
\[ = \dfrac{{2 \times 27}}{{200}}\]\[ = \dfrac{{27}}{{100}}\]

Note: Cube root need to group digit in no. 3 and taking the unit place digit of the first group & ten’s from \[I{I^{nd}}\].
In mathematics, a cube root of a number x is a number y such that \[\;{y^3}\; = \;x\]. All nonzero real numbers have exactly one real cube root and a pair of complex conjugate cube roots, and all nonzero complex numbers have three distinct complex cube roots. For example, the real cube root of 8, denoted \[\sqrt[3]{8}\], is 2, because \[{2^3}\; = \;8\]