Question

When 100 volt DC is applied across a solenoid, a current of 1.0 amp flows in it. When 100 volt AC is applied across the same coil, the current drops to 0.5 amp. If the frequency of the AC source is 50 Hz the impedance and inductance of the solenoid are:
$\text{A}\text{. }\! 200\Omega\text{ and }0.55H$
$\text{B}\text{. }\! 100\Omega\text{ and }0.86H$
$\text{C}\text{. }\! 200\Omega\text{ and }1.0H$
$\text{D}\text{. }\!100\Omega\text{ and }0.93H$

Answer 1

Hint: A DC voltage produces a constant current and the opposing quantity for the flow of the charges is resistance of the circuit. An Ac voltage source produces an alternating (oscillating) current in the circuit and the opposing quantity is not only resistance but the capacitance and inductance of the circuit also play a role in opposing the flow of charges and it is called the impedance of the circuit.

Complete step-by-step solution:
The full form of DC is direct current. It is the current flowing in the circuit with a constant potential difference. If the resistance of the circuit is R, the voltage of the DC source (e.g. a battery) is V, then the relation between V, R and the current i flowing in the circuit is given by ohm’s law i.e. $V=iR$. Consider the circuit as shown below:

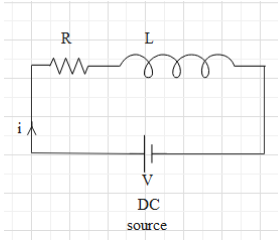
It is given that the voltage of the DC source is 100 volt and the current flowing in the circuit is 1 amp, so the resistance R of the circuit, according to ohm’s law will $R=\dfrac{V}{i}=\dfrac{100}{1}=100\Omega$. Therefore, the given circuit, which consists of a solenoid has a resistance of 100$\Omega$.
The full form of AC is alternating current. When a source produces an oscillating potential difference across the circuit, an alternating (oscillating current) flows in the circuit and this type of circuit is called an AC circuit. Since it is an oscillating circuit, it has a frequency (f).
Now consider an AC circuit as shown below:

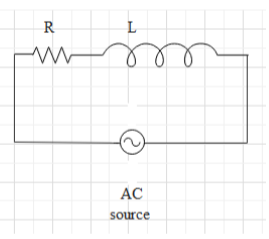
Like in a DC circuit, there is resistance (R) to resist the flowing charges (electrons), in an AC circuit also there is a resistance called impedance (Z). The relation between the potential difference (V), current (i) and the impedance (Z) of the circuit is $V=iZ$ …….(1). Therefore, impedance has the same unit as resistance i.e. $\Omega$
Now, you may be thinking why it is called impedance and not resistance. This is because in AC circuits other than the resistance of the circuit, other components (capacitor and inductor) also resist the flow of the charges. The capacitive resistance is equal to $\dfrac{1}{\omega C}$, where $\omega$ is the angular frequency of the circuit, which is equal to $2\pi f$ and C is the capacitance of the capacitor. The inductor resistance is equal to $\omega L$, where L is the inductance of the inductor.
If the circuit consists of an inductor (solenoid) of inductance L and ha some resistance R, then the impedance of the AC circuit is $Z=\sqrt{{{R}^{2}}+{{(\omega L)}^{2}}}$ ……..(2)
Let us now calculate the impedance of the circuit. From equation (1) we know
$Z=\dfrac{V}{i}$. Therefore, $Z=\dfrac{100}{0.5}=200\Omega$.
Since, the same solenoid is the resistance of the circuit will be the same. Hence, R=100$\Omega$. Substitute the values of Z and R in equation (2).
$\Rightarrow 200=\sqrt{{{\left( 100 \right)}^{2}}+{{(\omega L)}^{2}}}$
$\Rightarrow 40000={{\left( 100 \right)}^{2}}+{{(\omega L)}^{2}}$
$\Rightarrow 40000=10000+{{(\omega L)}^{2}}$
Therefore, $\omega L=\sqrt{30000}=173.2\Omega$. We know $\omega =2\pi f$ and
$f=50Hz$ and $\pi =3.14$. This implies that $\omega =2\times 3.14\times 50=314{{s}^{-1}}$.
$\therefore, L=\dfrac{173.2}{314}=0.55H$. The SI unit of inductance is henry (H).
Hence, the correct option is (A).

Note: The given voltage (potential difference) and the current of the AC circuit are the root mean square values of the voltage and the current in the circuit. In an AC circuit, the voltage and the current are continuously changing. The average of an oscillating function is zero and zero value of voltage and current will not help us in analysing the circuit components. That is why we calculate the root mean square values.