




What is the Difference Between Phase and Line Voltage?
Have you ever wondered how electricity flows in our homes, schools, and industries? Understanding the difference between line voltage and phase voltage is the key to knowing physics's basics of electrical systems. Whether you're a student preparing for exams or someone wanting to know how voltage works, this article breaks down the concept in the simplest way possible. Let’s learn the meaning, differences, and practical applications of line and phase voltage with real-world examples that will make this topic easy to understand. Let’s simplify physics together!
Line Voltage
Line voltage in a three-phase system is the potential difference between any two lines or phases present in the system, denoted by Vline or VL-L. The phases present here are conductors or windings of a coil. If R, Y and B are the three phases ( red phase, yellow phase, blue phase), then the voltage difference between R and Y, Y and B or B and R forms the line voltage.
Phase Voltage
Phase voltage, on the other hand, is the potential difference between one phase (R, Y or B) and the neutral junction point, denoted by Vphase = VR (voltage in red phase) = VY (voltage in yellow phase) = VB (voltage in blue phase).
Similarly line current is the current in one phase while phase current is the current inside the three-phase connection.
To understand line voltage and phase voltage relation, the first thing we need to understand is the different types of three-phase connection systems.
Relation Between Line Voltage and Phase Voltage in Star Connection
Star connection is also known as the three-phase four-wire system where there are 3 phases being involved and are connected by four wires. This is one of the most preferred systems for alternating current distribution whereas for transmission the Delta connection is used. In the star which is also denoted by Y the system of interconnection, the starting and the finishing points of the three coils are connected together to form the neutral point.
A three-phase voltage system, often arranged in a star connection, typically involves voltage flowing through three separate channels. For simplicity, these are referred to as Voltage in the Red Line ($V_R$), Voltage in the Yellow Line ($V_Y$), and Voltage in the Blue Line ($V_B$). The voltage in all three channels is equal and can be mathematically expressed as:
$ V_ph$ = $ V_R$ = $ V_Y$ = $ V_B$
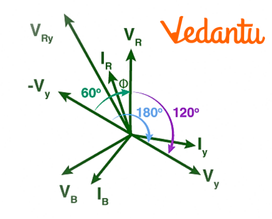
Here, line current = Phase Current
$I_R = I_Y = I_B = I_l$
If we extend $V_Y$ backward, we get $-V_Y$ and draw a resultant voltage of $V_R$ and $V_Y$, we get:
$ V_{RY} = V_R + (-V_Y)$
$ V_l = |V_{RY}| = \sqrt{V_R^2 + V_Y^2 + 2V_RV_Y\cos 60}$
$= \sqrt{V_{ph}^2 + V_{ph}^2 + 2V_{ph}V_{ph}\frac{1}{2}}$
Because
$\cos 60 = \dfrac{1}{2}$
Thus, we arrive at the relation between line voltage and phase voltage in star connection in an electric circuit:
$V_l = \sqrt{3} V_{ph}$
Relation Between Line Voltage And Phase Voltage In Delta Connection
The Delta connection is also said to be the Mesh connection where there is the presence of three phases connected with three wires. It is also one of the most preferred AC power systems for transmission.
In delta connection, all the three ends of the phases are connected to form a closed triangular loop, and it has no common neutral point as in a star connection. Here, the line and phase voltage are related as follows:
Vline=Vphase;
While line current = √3× phase current.
Difference Between Phase Voltage and Line Voltage
For Delta connection, the line voltage and phase voltage are equal.
Solved Examples
1. Calculate the phase voltage if the line voltage is 460 volts, given that the system is a three-phase balanced star connected system.
Answer: We know,
Vphase = Vline / √3 = 460 / √3 = 265.59 volts.
2. In which of the following circuit line voltage and phase voltage are equal? And what about the line voltage and phase voltage relationship in the other circuit?
Answer: As we know, in a delta connection (second figure), the line voltage and phase voltage are equal. While for a star connection line voltage is higher than phase voltage which is given by the relation: Vline = √3 Vphase.
Fun Facts
In any problem or question, the voltage given is generally line voltage. In the case of phase voltage, it should be mentioned. If not mentioned, consider it as the line voltage.
Our domestic three-phase power supply or 440 volts is the line voltage.
The single-phase 230 volts AC supply is the voltage difference between a phase and the neutral junction or rather the phase voltage.
The polyphase system where all the line voltages and line currents are equal is known as a three-phase balanced system. In the case of unsymmetrical loads, the system is generally an unbalanced one.
Conclusion
Understanding the difference between line voltage and phase voltage is crucial for working with electrical systems, especially in three-phase power setups. Line voltage measures the voltage between two lines, while phase voltage measures the voltage between a line and a neutral point. This knowledge helps in designing, troubleshooting, and optimizing electrical systems safely and effectively. Keep exploring and learning!
FAQs on Difference Between Line Voltage and Phase Voltage
1. What is the difference between phase and line voltage?
The primary difference is that phase voltage is the voltage measured between a phase (or line) and the neutral point, while line voltage is the voltage measured between any two lines in a three-phase system.
2. How is line voltage calculated from phase voltage?
In a star connection, the line voltage is $\sqrt{3}$ times the phase voltage. Mathematically:
Line Voltage = $\sqrt{3}$ × Phase Voltage.
3. Why is it important to understand the difference between line voltage and phase voltage?
Understanding this difference is crucial for designing, operating, and troubleshooting three-phase electrical systems efficiently and safely.
4. Where is line voltage used in practical applications?
Line voltage is commonly used for transmitting power in industrial and commercial setups because it supports higher power levels.
5. What is phase voltage, and where is it used?
Phase voltage refers to the voltage between a line and the neutral point. It is often used in residential and small-scale systems for devices requiring lower voltage.
6. Can line voltage and phase voltage be equal?
No, in a star connection, line voltage is always √3 times the phase voltage. However, in a delta connection, they are equal because there is no neutral point.
7. What is the relationship between line voltage and phase voltage in a star connection?
In a star connection:
Line Voltage = $\sqrt{3}$ × Phase Voltage.
This is a key formula to understand three-phase systems.
8. How does a star connection affect the difference between line voltage and phase voltage?
In a star connection, the neutral point allows the phase voltage to be lower than the line voltage by a factor of $\sqrt{3}$.
9. Why is the difference between phase and line voltage important in three-phase systems?
This difference determines the system’s voltage levels, which affects its efficiency, safety, and application in electrical networks.
10. How can Vedantu help understand the difference between line and phase voltage?
Vedantu provides easy-to-understand lessons, expert guidance, and interactive resources to help students and learners grasp concepts like the difference between line voltage and phase voltage with clarity.























