




Bohr Magneton Formula and Step-by-Step Derivation
The Bohr magneton represents a fundamental constant in atomic physics, quantifying the intrinsic magnetic moment of an electron. Named after physicist Niels Bohr, this quantum unit emerges from Bohr's atomic model and serves as the standard for measuring magnetic moments in atoms, molecules, and elementary particles across various physical phenomena.
Understanding Magnetic Moments in Atomic Systems
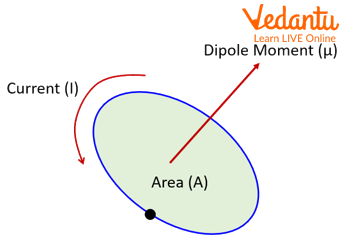
Before exploring the Bohr magneton specifically, we must understand the concept of magnetic dipole moment. When charged particles move in circular orbits, they create current loops that generate magnetic fields. The magnetic moment quantifies this magnetic strength and orientation.
The bohr magneton definition emerges from the classical treatment of an electron orbiting the nucleus. As electrons possess both charge and angular momentum, their orbital motion produces a measurable magnetic moment. This quantum mechanical property becomes particularly significant when atoms interact with external magnetic fields.
Bohr Magneton Formula and Mathematical Foundation
The bohr magneton formula can be derived through classical electromagnetic principles combined with quantum mechanical constraints. For an electron moving in a circular orbit with velocity $v$ and radius $r$, we can establish the relationship between its magnetic moment and angular momentum.
Consider an electron with charge $-e$ moving in a circular path. The orbital period is given by:
This circular motion creates an equivalent current:
The magnetic moment of this current loop equals the current multiplied by the enclosed area:
Quantum Mechanical Considerations
Bohr's quantum condition states that angular momentum is quantized in discrete units. The orbital angular momentum becomes:
Substituting this relationship into our magnetic moment expression:
For the ground state hydrogen atom (n = 1), the minimum quantized angular momentum gives us the fundamental magnetic moment unit:
This can also be written using the reduced Planck constant $\hbar = \frac{h}{2\pi}$:
Bohr Magneton Value and Units
The bohr magneton value represents one of the fundamental constants in physics. Using the accepted values of elementary charge, reduced Planck constant, and electron mass:
| Quantity | Value | Units |
|---|---|---|
| Bohr magneton ($\mu_B$) | 9.274 × 10⁻²⁴ | J/T |
| Bohr magneton ($\mu_B$) | 9.274 × 10⁻²⁴ | A·m² |
| Bohr magneton in eV/T | 5.788 × 10⁻⁵ | eV/T |
The bohr magneton units can be expressed in two equivalent forms: Joules per Tesla (J/T) or Ampere-square meters (A·m²). Both represent magnetic dipole moment dimensions in the SI system.
Bohr Magneton Value in eV
For atomic and molecular calculations, the bohr magneton value in ev proves particularly useful. Converting from Joules to electron volts:
This energy unit becomes essential when calculating Zeeman effect energy shifts and magnetic field interactions in spectroscopy applications.
Nuclear Magneton and Comparative Analysis
The nuclear magneton serves as the magnetic moment unit for heavier particles like protons and neutrons. Since the nuclear magneton depends on proton mass rather than electron mass:
The ratio between Bohr magneton and nuclear magneton equals the mass ratio:
This fundamental relationship explains why electronic magnetic moments dominate over nuclear contributions in most atomic phenomena.
Applications in Modern Physics
The Bohr magneton finds extensive applications across multiple physics domains:
FAQs on What is the Bohr Magneton? Definition, Value, and Significance in Physics
1. What is the Bohr magneton and why is it important?
The Bohr magneton is a physical constant that represents the natural unit of the magnetic moment of an electron caused by its orbital or spin motion.
- It is denoted by the symbol μB.
- The value of Bohr magneton is approximately 9.274 × 10-24 A·m² (ampere square meter).
- This constant helps in explaining magnetic properties at the atomic level, especially in quantum physics and atomic structure.
- Important for understanding the magnetic moments in atoms and phenomena such as electron spin and paramagnetism.
2. What is the formula for the Bohr magneton?
The Bohr magneton is given by the formula:
μB = (eħ) / (2me), where:
- e = elementary charge (1.602 × 10-19 C)
- ħ = reduced Planck's constant
- me = mass of electron
3. Why is the Bohr magneton used in atomic physics?
The Bohr magneton is used as a standard unit for measuring the magnetic moment of electrons in atoms.
- Helps analyze electron spin and orbital angular momentum.
- Essential in studying magnetism and explaining properties like paramagnetism and diamagnetism.
- Connects quantum mechanics with magnetic properties in the CBSE physics syllabus.
4. What are the applications of the Bohr magneton?
Bohr magneton is widely applied in various areas of physics and chemistry:
- Determining atomic and molecular magnetic moments.
- Studying electron configurations in atoms.
- Explaining magnetic behavior of materials (ferromagnetism, paramagnetism, diamagnetism).
- Used in nuclear magnetism and electron magnetic resonance experiments.
5. How does the Bohr magneton value compare to the nuclear magneton?
The Bohr magneton is much larger than the nuclear magneton.
- Bohr magneton (μB): About 9.274 × 10-24 A·m²
- Nuclear magneton (μN): About 5.05 × 10-27 A·m²
- Thus, μB is roughly 1836 times larger, showing significant difference linked to particle mass (electron vs. proton).
6. Derive the expression for Bohr magneton from basic principles.
The Bohr magneton (μB) can be derived by considering an electron orbiting the nucleus:
- Magnetic moment (μ): μ = (current) × (area)
- For a circular orbit, μ = (eωr2) / 2
- From quantization, angular momentum L = nħ, and for n=1 (ground state): L = ħ
- Substitute values to get μB = (eħ)/(2me)
7. What is the value of the Bohr magneton according to the CBSE syllabus?
According to the latest CBSE Physics syllabus, the value of the Bohr magneton (μB) is:
- μB = 9.274 × 10-24 A·m² (ampere square meter)
- Also written as 9.274 × 10-24 J/T (joule per tesla)
- This value should be used in all exam-related solutions and calculations.
8. What is the significance of the negative sign in the magnetic moment of the electron?
The negative sign in the magnetic moment of the electron indicates that the direction of the magnetic moment is opposite to the angular momentum due to the negative charge of the electron.
- Important in understanding electron spin and Stern-Gerlach experiment results.
- This property is crucial in quantum mechanics and aligns with the physical behavior observed in atomic models.
9. Can you explain the historical background of the Bohr magneton?
The Bohr magneton was introduced by Niels Bohr in 1913 as part of his model of the atom.
- It provided a fundamental quantum unit to describe the magnetic moment of an electron.
- Became critical for the development of quantum mechanics and the study of atomic structure.
- Still serves as a standard reference value in modern physics and chemistry.
10. How does the Bohr magneton relate to electron spin and orbital motion?
Bohr magneton is the unit to measure magnetic moment arising from both electron spin and its orbital motion around the nucleus.
- Each electron's spin magnetic moment and orbital magnetic moment are multiples of μB.
- This relationship is key in topics like atomic structure and magnetic properties of materials.























