Score Higher with Class 9 Number Systems Exercise 1.2 Solutions Practice
NCERT Solutions for Class 9 Maths Chapter 1 Number Systems
FAQs on NCERT Solutions for Class 9 Maths Chapter 1 Number Systems
1. What does class 9 maths chapter 1 exercise 1.2 focus on in number systems?
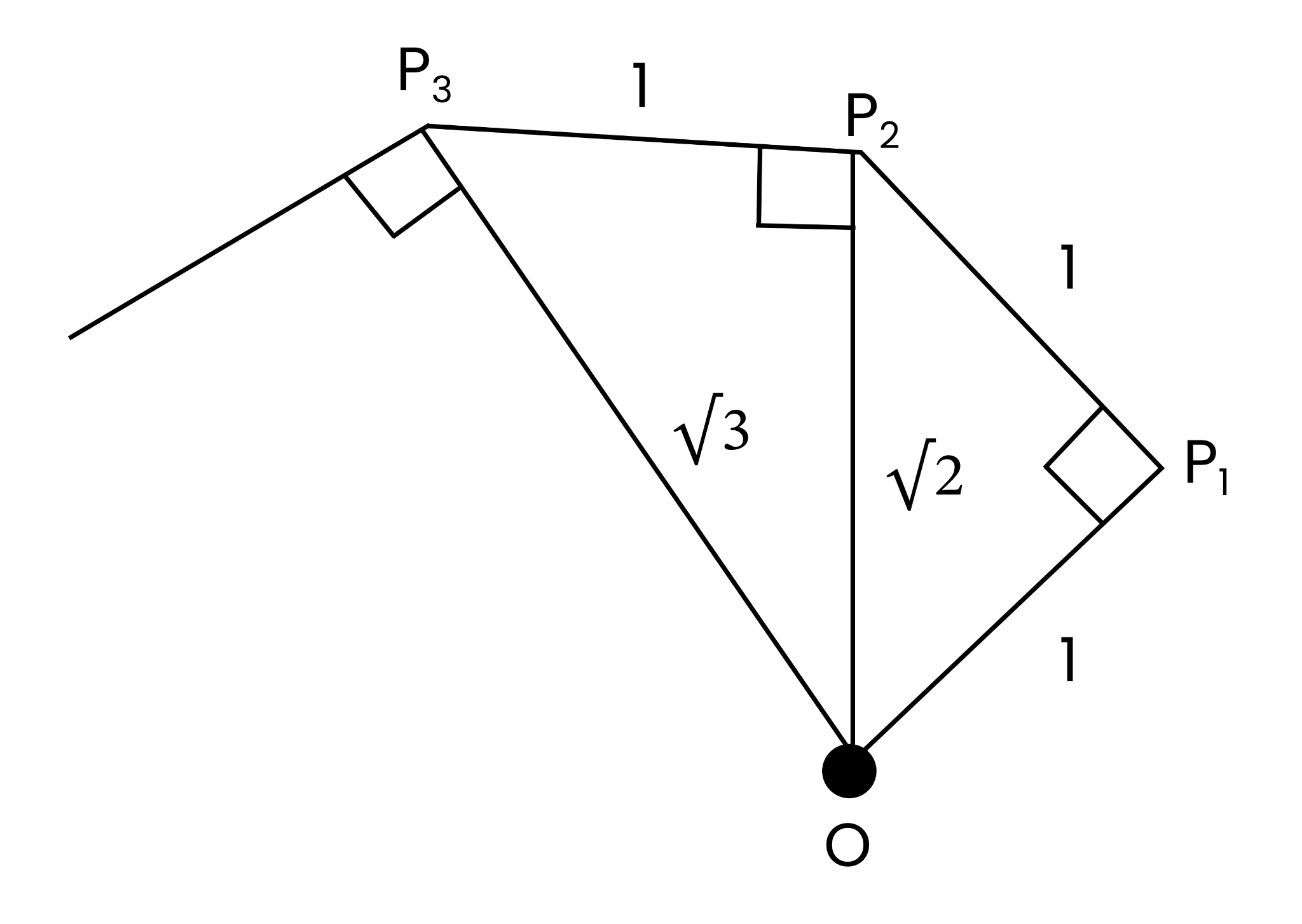
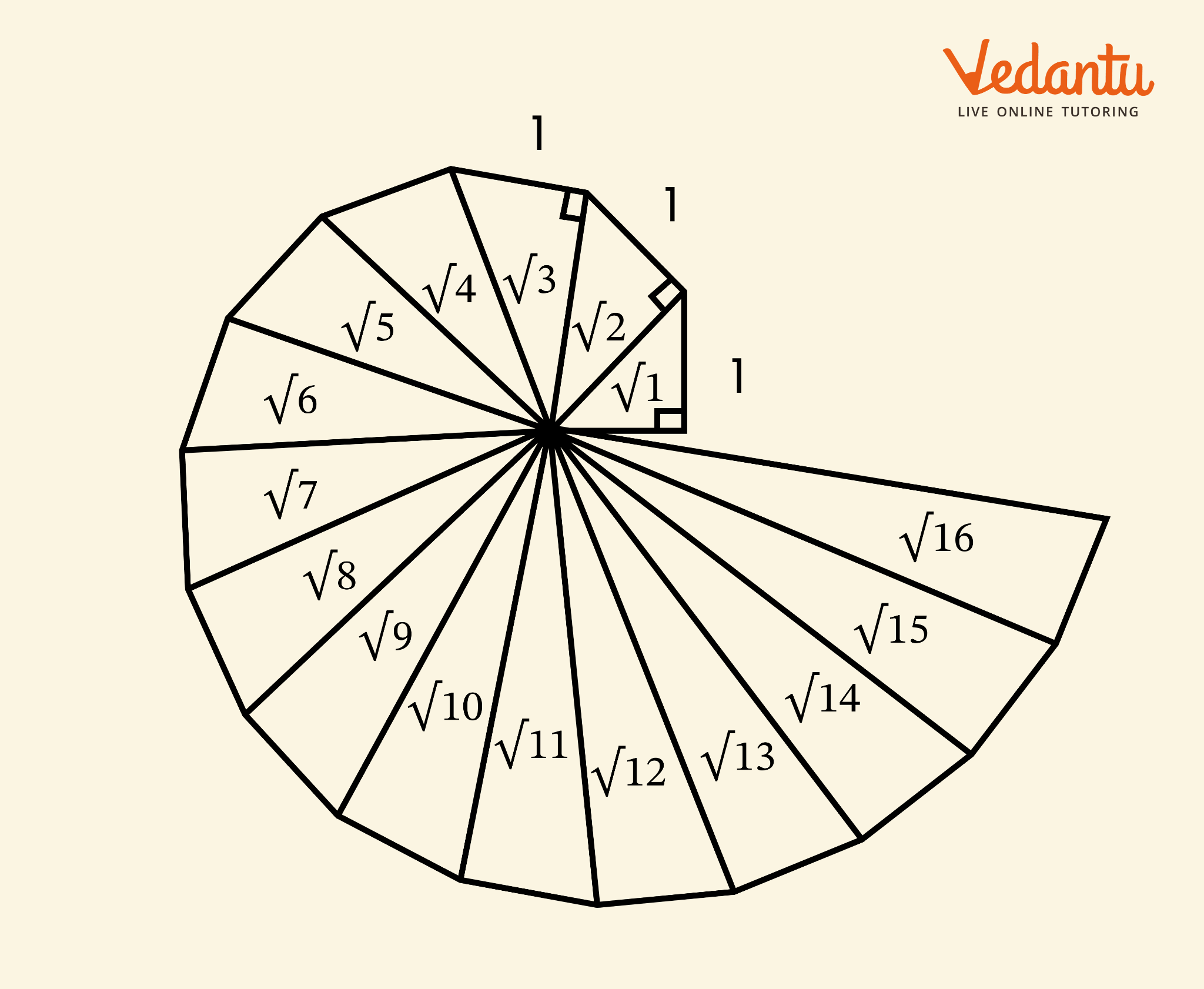
Exercise 1.2 in Chapter 1 Number Systems focuses on the decimal representation of rational numbers. Students learn to express rational numbers in decimal form and understand terminating and non-terminating decimal expansions through various problem-solving techniques.
2. How do NCERT Solutions help students solve decimal representation problems in number systems?
NCERT Solutions provide step-by-step methods to convert rational numbers into decimal form and identify patterns in decimal expansions.
Understanding decimal representations is crucial for advanced mathematical concepts and real-world applications.
3. Which types of rational numbers have terminating decimal representations?
Rational numbers have terminating decimal representations when their denominators (in lowest terms) contain only factors of 2 and 5. This is because our decimal system is base 10, and numbers divisible by powers of 10 result in finite decimal places.
4. What content is included in the Free PDF of class 9 number systems exercise 1.2 solutions?
The Free PDF contains complete solutions for all exercise 1.2 questions covering decimal representation of rational numbers.
Students get comprehensive coverage of decimal conversion techniques and problem-solving strategies in a downloadable format.
5. How can students identify non-terminating recurring decimals in rational numbers?
Students can identify non-terminating recurring decimals when the denominator of a rational number (in simplest form) has prime factors other than 2 and 5. These decimals show repeating patterns after performing long division.
6. Why do students benefit from using Vedantu's NCERT Solutions for number systems practice?
Vedantu's solutions provide clear explanations and systematic approaches to solve decimal representation problems effectively.
Students develop strong conceptual understanding and improve their problem-solving speed for competitive exams.
7. What is the difference between terminating and non-terminating decimals?
Terminating decimals have a finite number of digits after the decimal point (like 0.25), while non-terminating decimals continue infinitely. Non-terminating decimals can be recurring (showing repeating patterns) or non-recurring (like π).
8. How does exercise 1.2 prepare students for advanced number system concepts?
Exercise 1.2 builds fundamental skills in decimal representation that form the basis for advanced mathematical topics.
These concepts are essential for algebra, geometry, and higher-level mathematics in subsequent classes.
9. Can students access class 9 maths number systems exercise 1.2 solutions offline?
Yes, students can download the Free PDF format of exercise 1.2 solutions for offline access. This allows convenient study without internet connectivity and enables printing for handwritten practice and revision.
10. How do recurring decimals help students understand rational number properties?
Recurring decimals demonstrate that all rational numbers have predictable decimal patterns, either terminating or repeating infinitely.
This concept distinguishes rational numbers from irrational numbers and builds number system comprehension.














 Watch Video
Watch Video