How to Write Stepwise Answers & Diagrams for Parallel and Intersecting Lines
FAQs on NCERT Solutions For Class 7 Maths Chapter 5 Parallel & Intersecting Lines (2025-26)
1. What are NCERT Solutions for Class 7 Maths Chapter 5: Parallel and Intersecting Lines?
NCERT Solutions for Class 7 Maths Chapter 5: Parallel and Intersecting Lines provide fully solved, stepwise answers for all textbook exercises, helping students master key concepts.
Main features include:
- Detailed solutions for every question in Chapter 5
- Clear definitions of parallel lines, intersecting lines, and related terms
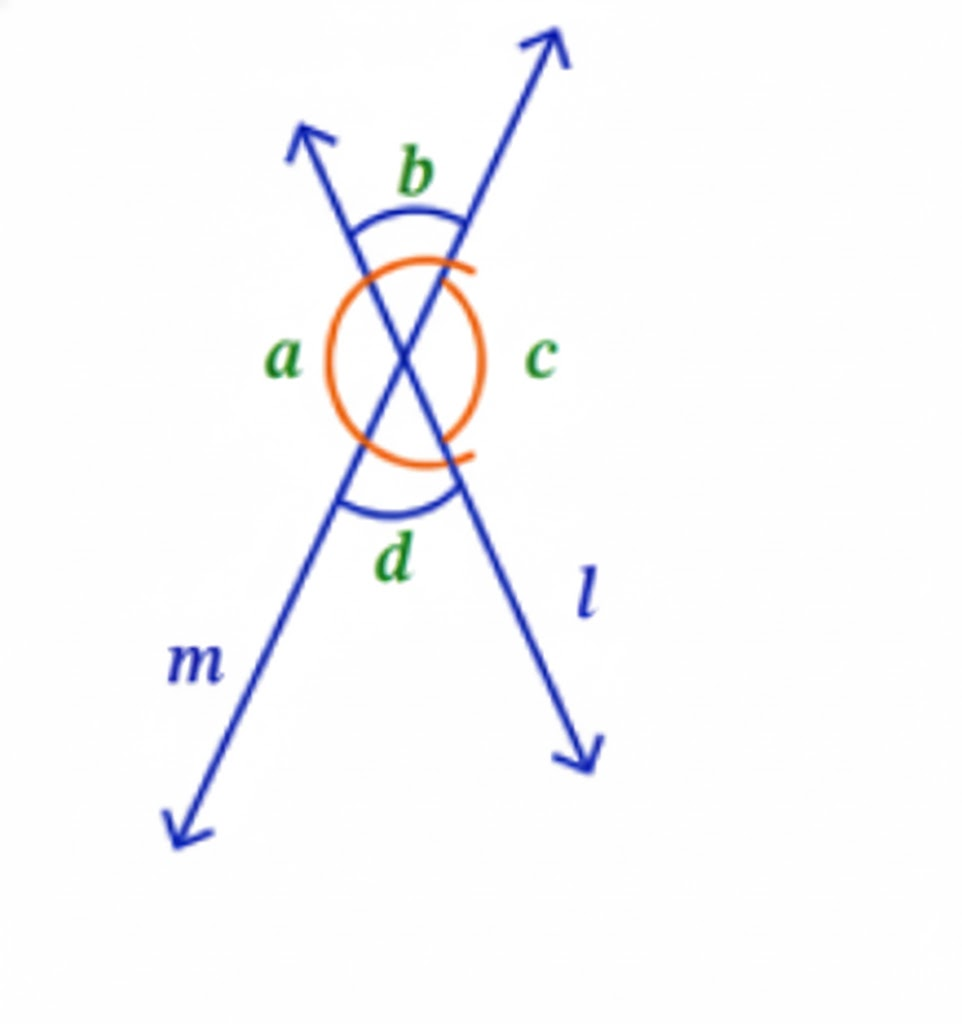
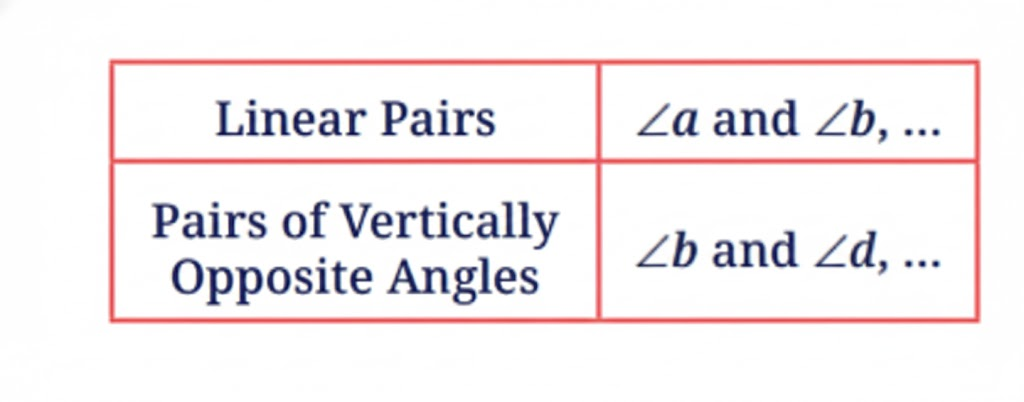
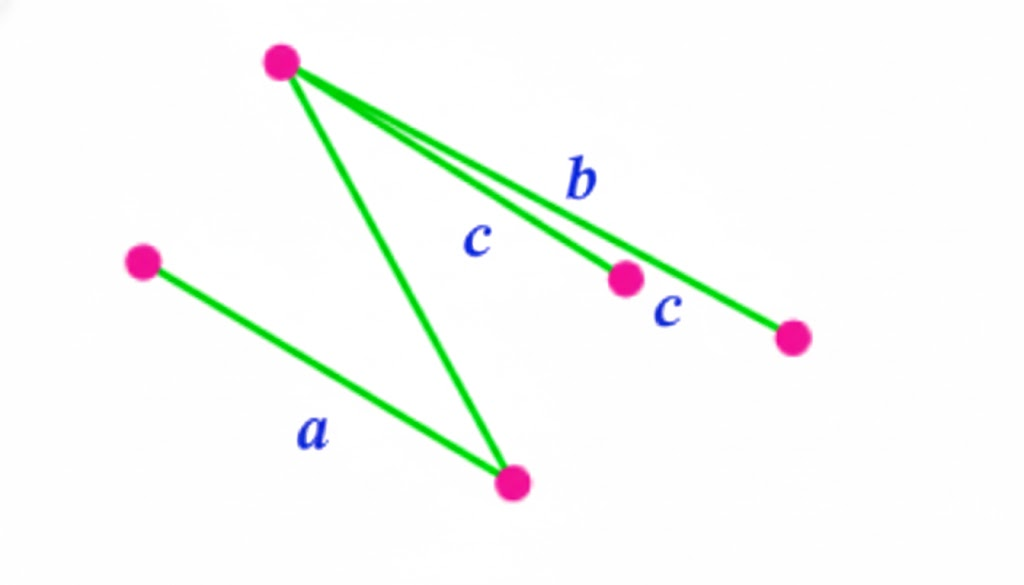
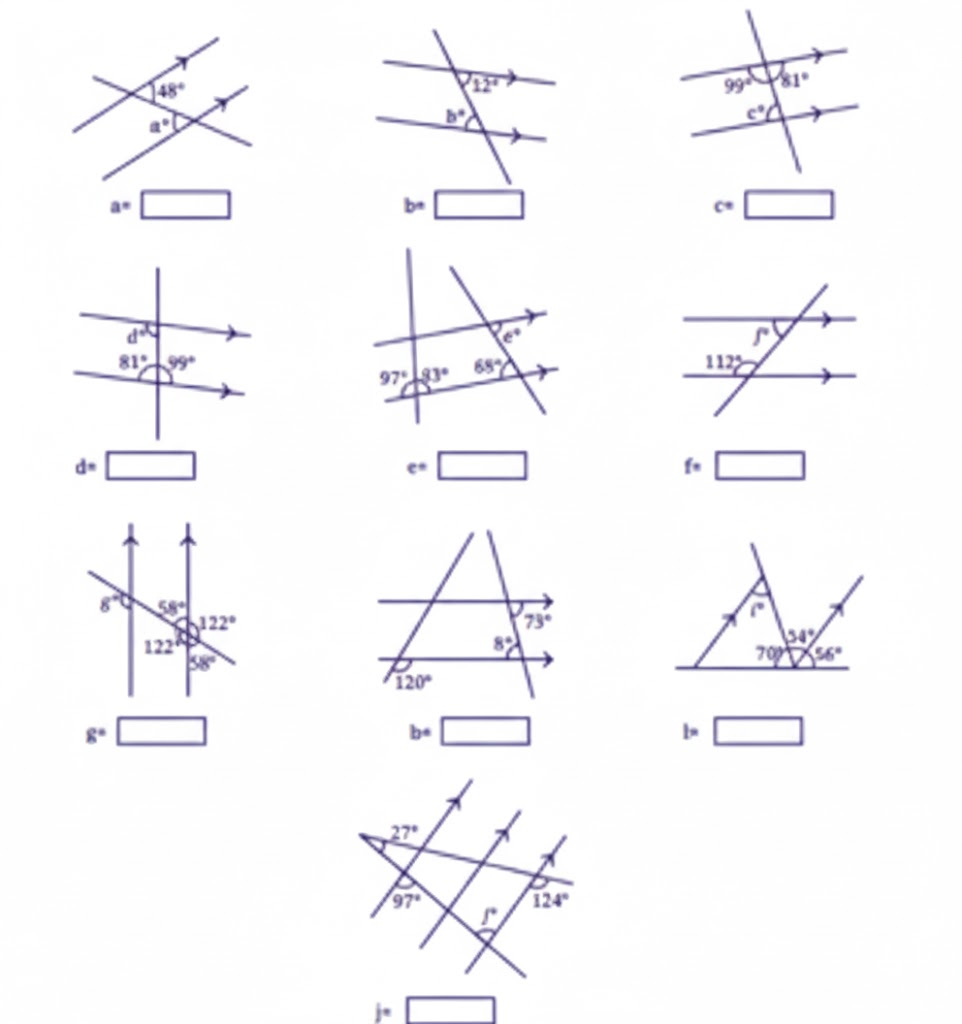
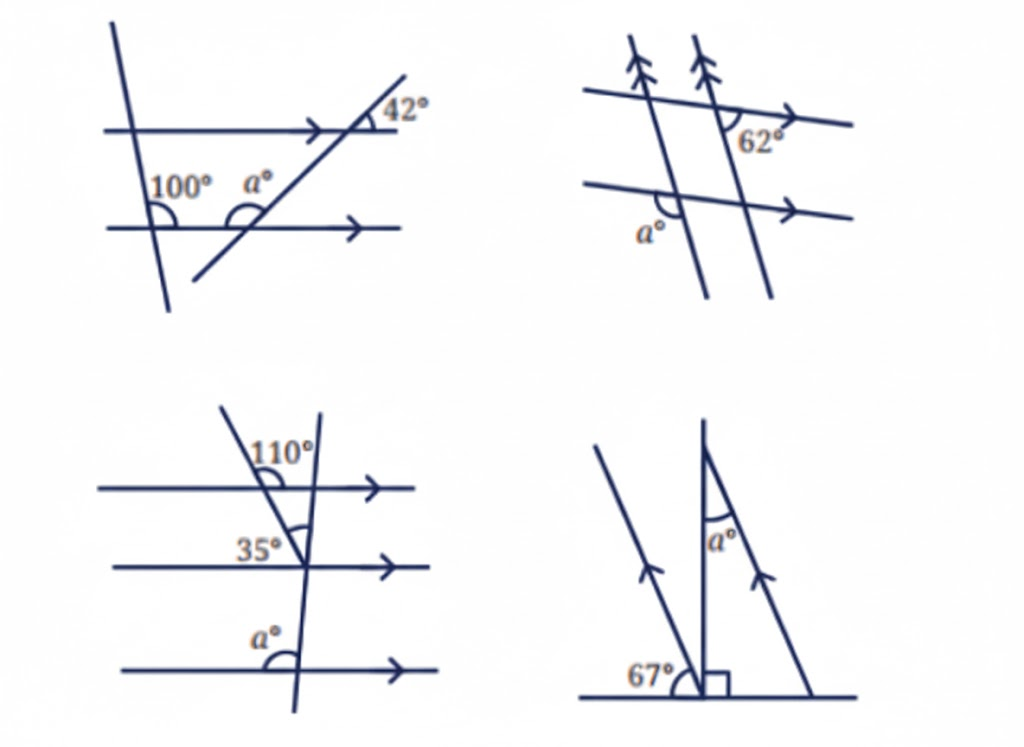
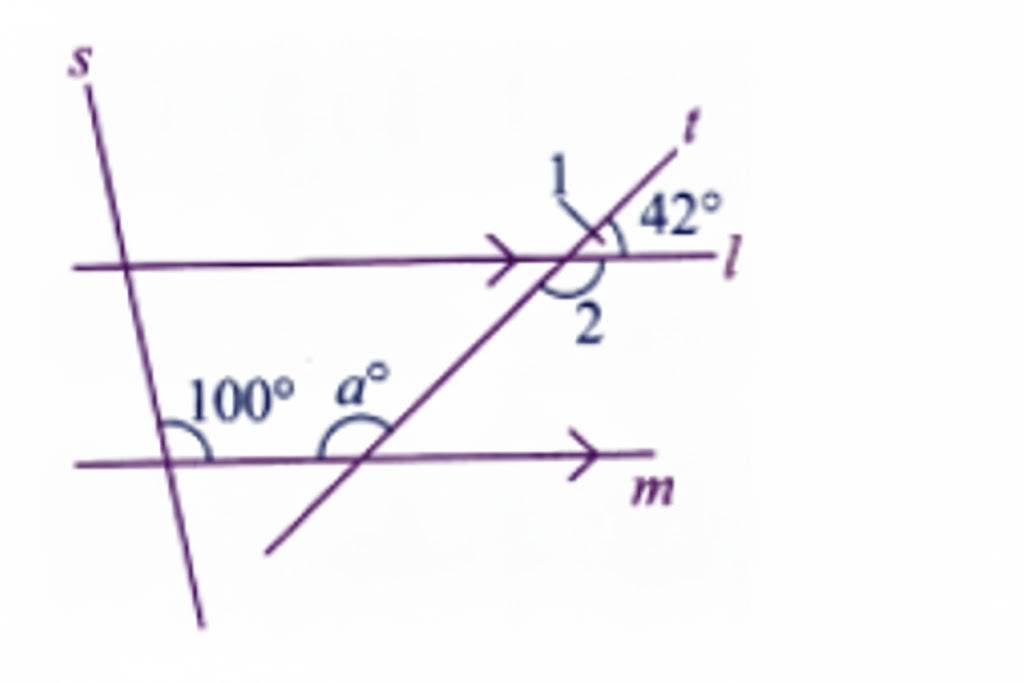
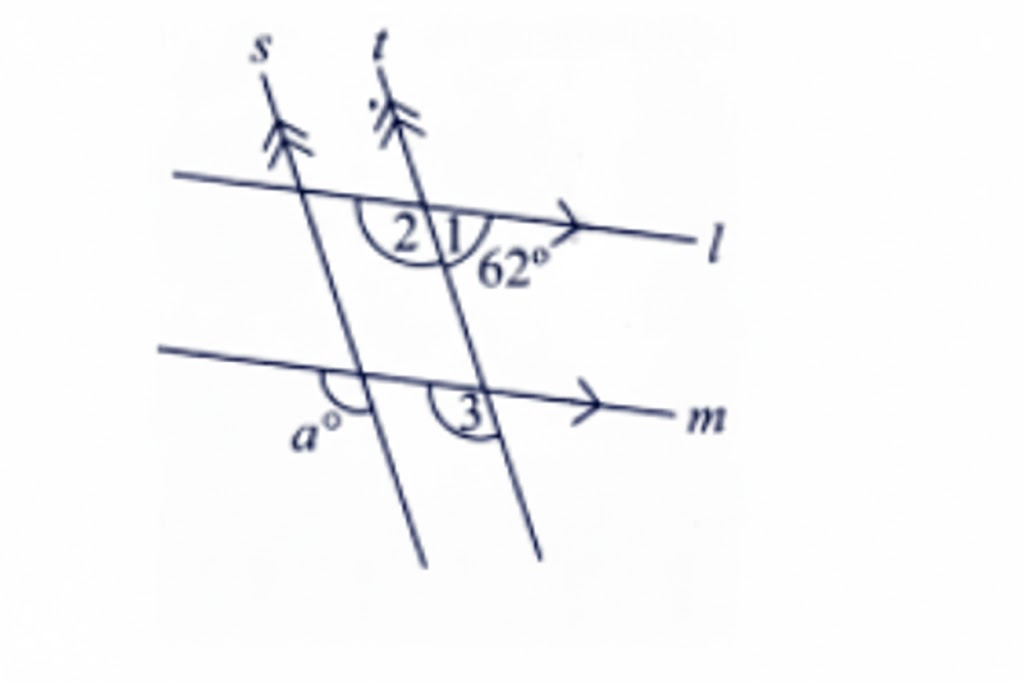
- Diagrams and labelling tips for accurate answers
- Aligned to the 2025–26 CBSE syllabus for Class 7 Maths
- Free, downloadable PDF format for offline study
2. How do stepwise NCERT Solutions help Class 7 students score better in Maths exams?
Stepwise NCERT Solutions ensure students write answers in a manner that matches the CBSE marking scheme, leading to higher scores.
Benefits include:
- Allocation of marks for each step
- Increased clarity and logical flow in answers
- Higher chances of securing full marks
- Helps avoid missing out on steps or keywords
- Makes revision easier using clear solutions
3. Are diagrams and definitions compulsory in Class 7 Maths Chapter 5 answers?
Yes, including neat diagrams and precise definitions is essential for scoring full marks in Chapter 5.
Best practices:
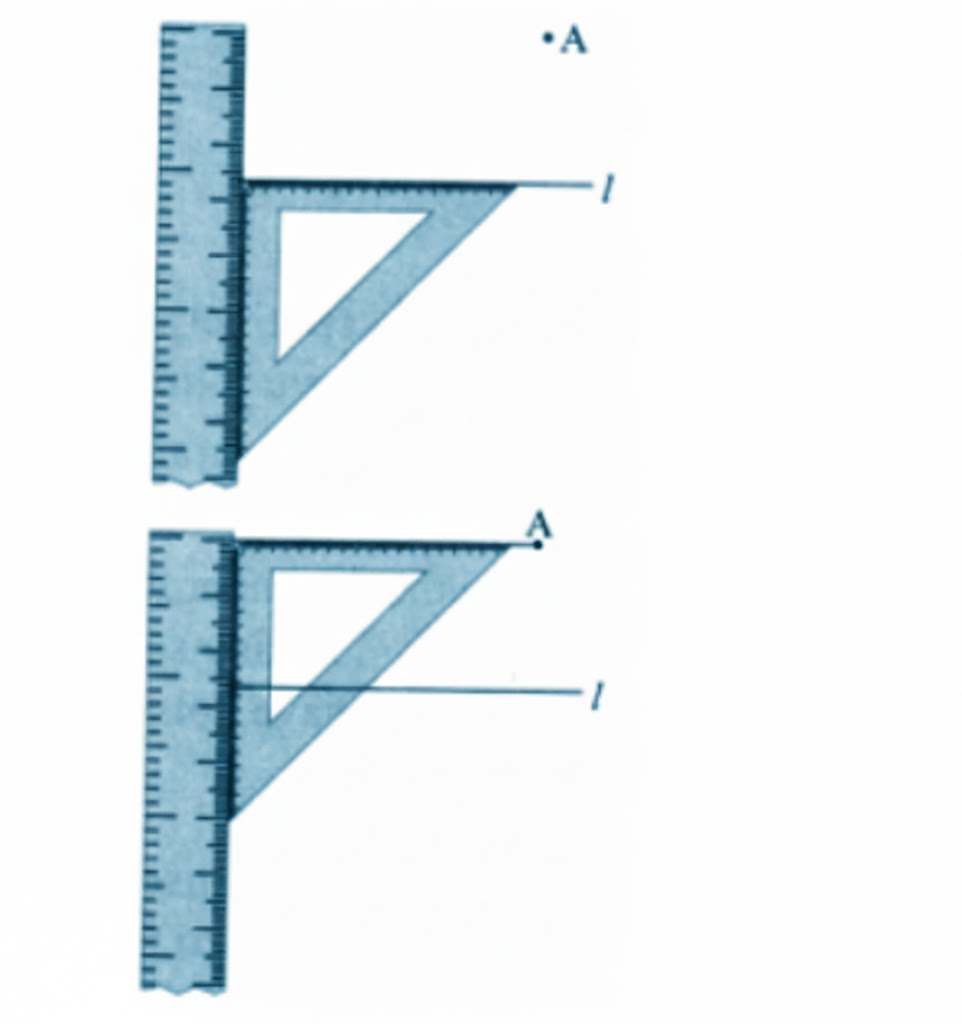
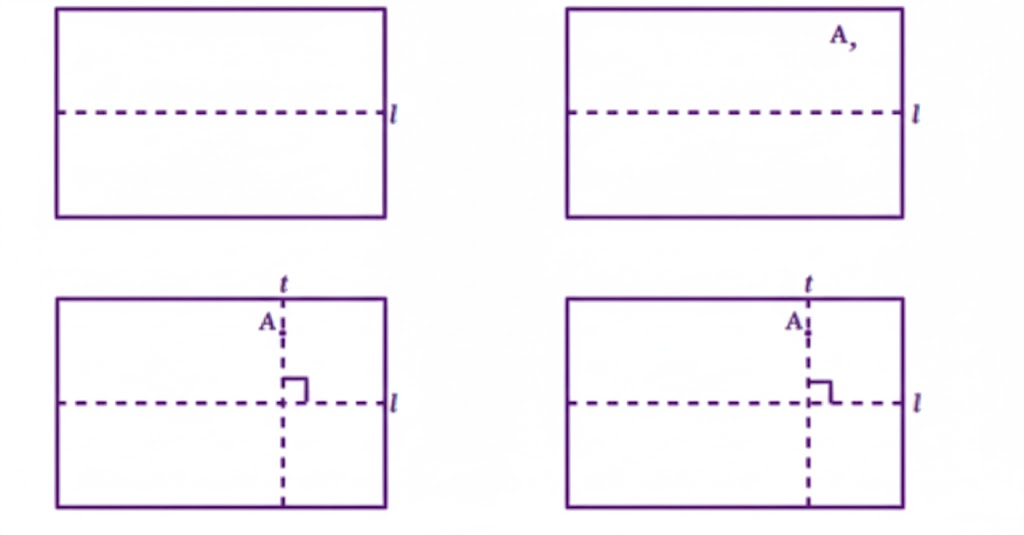
- Always draw and label diagrams for questions involving lines, points, or angles
- Start answers with correct definitions where required
- Use geometrical conventions for lines and points
- Diagrams help in visual understanding and attract step marks
4. Where can I download the NCERT Solutions for Class 7 Maths Chapter 5 PDF?
You can easily download the free PDF of Class 7 Maths Chapter 5 NCERT Solutions from trusted educational websites.
Steps:
- Look for the download button on the solutions page
- Choose the 2025–26 syllabus
- PDF includes exercise-wise, stepwise answers for offline study
5. What are the most important definitions and formulae from Class 7 Maths Chapter 5?
The crucial definitions and formulae from Chapter 5 include:
Key terms:
- Parallel Lines: Lines that never meet, even if extended infinitely.
- Intersecting Lines: Lines that cross at exactly one point.
- Transversal, Angle Pairs: Alternate, corresponding, and interior angles.
- Basic formulae relate to angle sums formed by these lines.
Remember to write these accurately for full marks.
6. How can I revise Class 7 Maths Chapter 5 Parallel and Intersecting Lines quickly before exams?
Quick revision of Chapter 5 is possible by focusing on key concepts, diagrams, and step-by-step solved questions.
Revision plan:
- Day 1: Revise definitions and basic concepts
- Day 2: Practice exercise-wise solutions and diagrams
- Day 3: Solve important questions and take mock tests
- Use flash notes and summary tables for quick recall
7. Which questions from Class 7 Maths Chapter 5 are most likely to appear in CBSE exams?
CBSE exams often include questions from definitions, simple construction, and application of properties in Chapter 5.
Likely question types:
- Define parallel and intersecting lines
- Identify angles formed by a transversal
- Draw and label diagrams
- Prove lines are parallel using angle properties
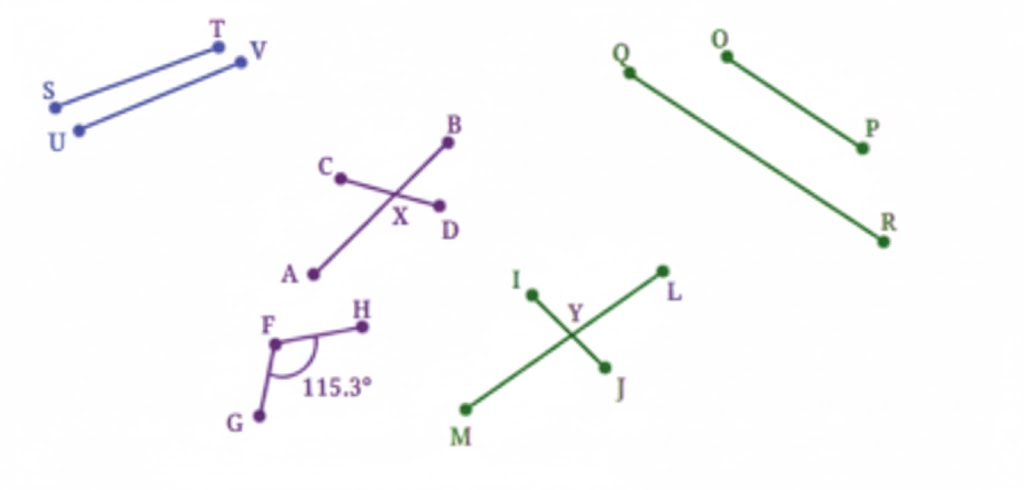
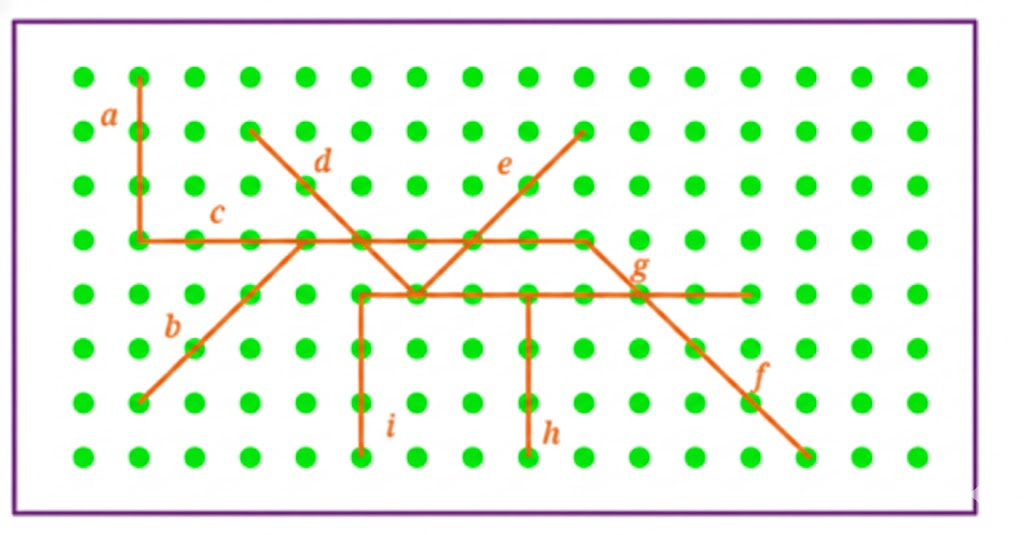
- Name pairs of parallel and intersecting lines from a given figure
8. How should Class 7 students write long answers for Parallel and Intersecting Lines to maximise exam marks?
For long answers, structure your solution with definitions, labelled diagrams, and stepwise explanations.
Tips for full marks:
- Start with a clear definition
- Use a neat, labelled diagram
- Explain each step logically and in the order asked
- Highlight key terms (like parallel lines, transversal, etc.)
- Conclude with the required statement (e.g., reasons or proof)
9. Are NCERT Solutions enough for Class 7 Maths exams?
NCERT Solutions provide a strong foundation as they cover all textbook questions in a CBSE-aligned manner.
To score even better:
- Complete all NCERT textbook exercises
- Practice extra questions and previous year papers
- Use exemplar problems for higher-order thinking
- Revise definitions, formulae, and diagrams regularly
10. Do examiners award partial marks for correct steps even if the final answer is wrong?
Yes, as per CBSE marking scheme, partial marks are awarded for all correct steps shown, even if the final answer is incorrect.
Tips:
- Always show all steps clearly
- Use correct mathematical reasoning
- Write formulae and working wherever needed
- This ensures you get marks for your process, not just the final answer
11. What topics does Chapter 5 Parallel and Intersecting Lines cover in Class 7 Maths?
Chapter 5 covers the basic properties, definitions, and differences between parallel and intersecting lines.
Main topics:
- Parallel lines, intersecting lines
- Drawing and identifying lines in figures
- Properties of angles formed by transversals
- Real-life examples and application-based problems
12. How do you label diagrams in Class 7 Maths Chapter 5 for full marks?
Labelling diagrams accurately is crucial for scoring well in Maths Chapter 5.
Checklist:
- Draw straight lines using a ruler
- Name lines (like AB, CD) and points clearly
- Mark angles if required
- Use correct geometric conventions
- Keep diagrams clean and clear for examiner readability