Algebraic Expressions - Exercise-wise Questions and Answers For Class 7 Maths - Free PDF Download
FAQs on NCERT Solutions For Class 7 Maths Chapter 10 Algebraic Expressions - 2025-26
1. What are the key topics a student must master in NCERT Class 7 Maths Chapter 10, Algebraic Expressions?
According to the CBSE 2025-26 syllabus, a student must master the following key topics in Chapter 10, Algebraic Expressions:
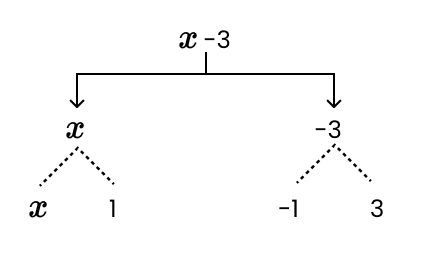
- Identifying variables and constants to form expressions.
- Understanding the components of an expression, such as terms, factors, and coefficients.
- Classifying expressions as monomials, binomials, or trinomials.
- Differentiating between like and unlike terms.
- Performing operations like addition and subtraction of algebraic expressions.
- Finding the value of an expression by substituting the given values for variables.
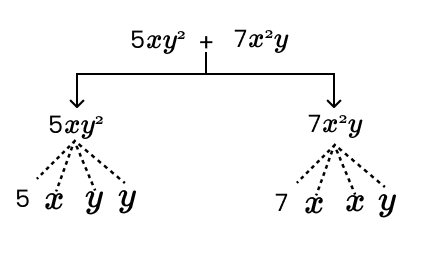
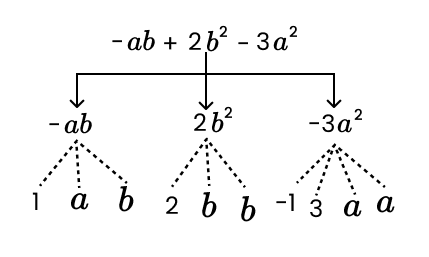
2. How do you correctly identify terms and their factors in an expression like 5xy² + 7x²y?
To correctly identify terms and factors, you first separate the parts of the expression connected by addition or subtraction. These are the terms. Then, you break down each term into its constituent parts that are multiplied together.
- Step 1: Identify the terms. In the expression 5xy² + 7x²y, the terms are 5xy² and 7x²y.
- Step 2: Identify the factors for each term.
- For the term 5xy², the factors are 5, x, y, and y.
- For the term 7x²y, the factors are 7, x, x, and y.
3. Why is it essential to distinguish between 'like' and 'unlike' terms before adding or subtracting expressions?
It is essential to distinguish between like and unlike terms because addition and subtraction can only be performed on like terms. Like terms have the same variables raised to the same power, acting as a common unit. For instance, in '3x + 2x', both terms represent multiples of 'x', so they can be combined to '5x'. However, in '3x + 2y', the variables are different, so they cannot be combined further. Treating unlike terms as like terms is a fundamental error that leads to incorrect simplification.
4. What is the correct method to find the numerical coefficient of a term in an expression?
The numerical coefficient is the constant number multiplied by the variable part of a term. To find it, simply identify the numerical factor in that term. For example, in the expression 100m + 1000n:
- For the term 100m, the numerical coefficient is 100.
- For the term 1000n, the numerical coefficient is 1000.
- In a term like -p²q², the numerical coefficient is -1, as the term implies -1 × p²q².
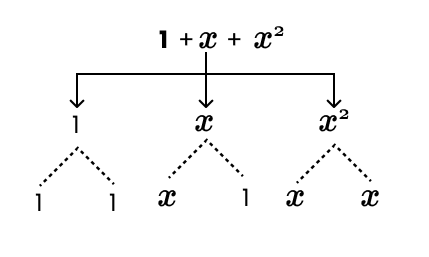
5. How do you classify an algebraic expression as a monomial, binomial, or trinomial?
You classify an algebraic expression based on the number of unlike terms it contains:
- An expression with only one term is called a monomial (e.g., 7mn, y²).
- An expression with two unlike terms is called a binomial (e.g., 4y - 7z, a² + b²).
- An expression with three unlike terms is called a trinomial (e.g., x + y - xy, z² - 3z + 8).
A constant like '100' is also considered a monomial because it consists of a single term.
6. What is a common mistake students make when subtracting one algebraic expression from another?
A very common mistake when subtracting algebraic expressions is failing to change the sign of every term in the expression being subtracted. For example, to subtract (4a - 7ab + 3b + 12) from (12a - 9ab + 5b - 3), you must reverse the sign of each term inside the second parenthesis before combining like terms.
- Correct Method: (12a - 9ab + 5b - 3) - (4a - 7ab + 3b + 12)
- Sign Change: 12a - 9ab + 5b - 3 - 4a + 7ab - 3b - 12
- Final Answer: 8a - 2ab + 2b - 15
Forgetting to change '+12' to '-12' or '-7ab' to '+7ab' is a frequent error.
7. How do you solve questions from Exercise 10.2 that require finding the value of an expression?
To find the value of an expression for a given variable, you must follow a two-step process:
- Step 1: Simplify the expression. Combine all like terms to make the expression as simple as possible. For example, simplify 3(x + 2) + 5x - 7 to 8x - 1.
- Step 2: Substitute the given value. Replace the variable in the simplified expression with its given numerical value and perform the arithmetic operations. If x = 2, then 8x - 1 becomes 8(2) - 1, which equals 16 - 1 = 15.
Always simplify first to reduce the chance of calculation errors.
8. How do the concepts from Chapter 10, Algebraic Expressions, apply in higher-level mathematics?
The concepts in Chapter 10 are foundational for almost all of higher-level mathematics. Mastering how to form, simplify, and evaluate expressions is crucial for:
- Solving Equations: In higher classes, you will solve linear, quadratic, and polynomial equations, all of which are built from algebraic expressions.
- Functions: The study of functions in calculus and advanced algebra relies on understanding how to manipulate expressions.
- Physics and Engineering: Formulas used in science, like F=ma or E=mc², are algebraic expressions that describe relationships between physical quantities.
A strong grasp of this chapter ensures a smoother transition to more complex topics.
9. How do NCERT Solutions for Chapter 10 help in mastering Algebraic Expressions?
The NCERT Solutions for Class 7 Maths Chapter 10 are a vital tool for mastering the topic. They provide step-by-step methods for solving every problem in the textbook exercises. By studying these solutions, students can understand the correct procedure for identifying terms, combining like terms, and evaluating expressions, ensuring they follow the CBSE-prescribed methodology. This helps in identifying weak areas and correcting mistakes before exams.