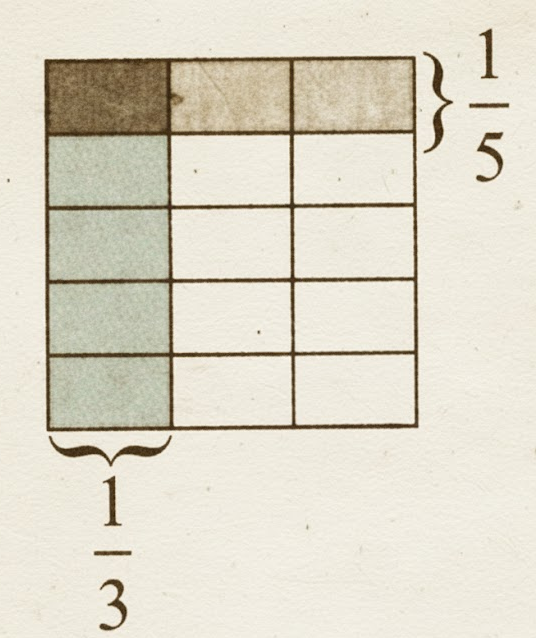
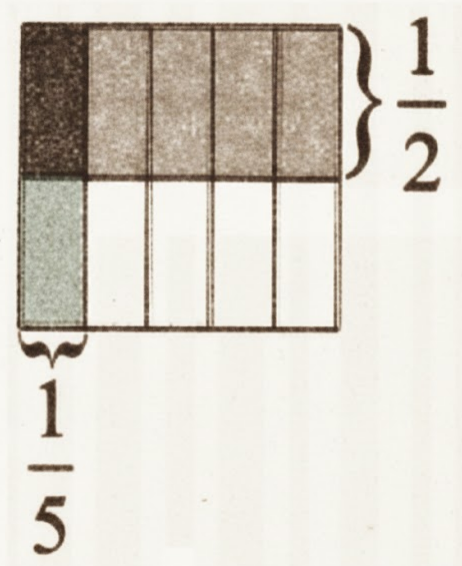
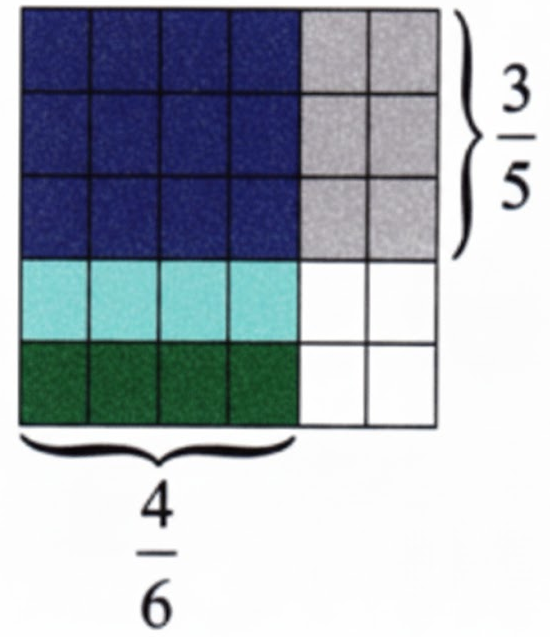
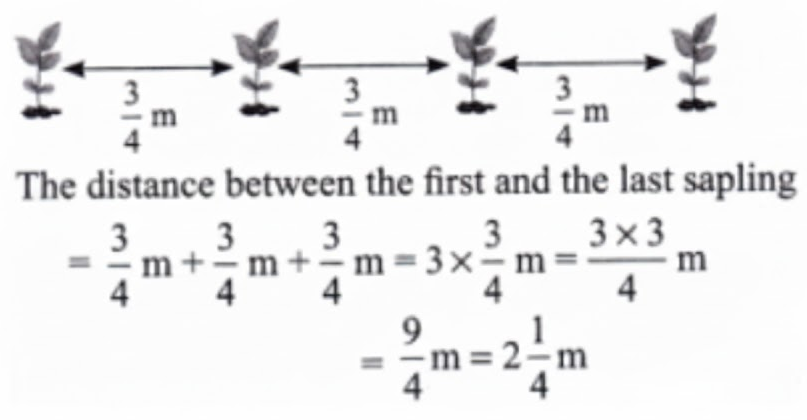
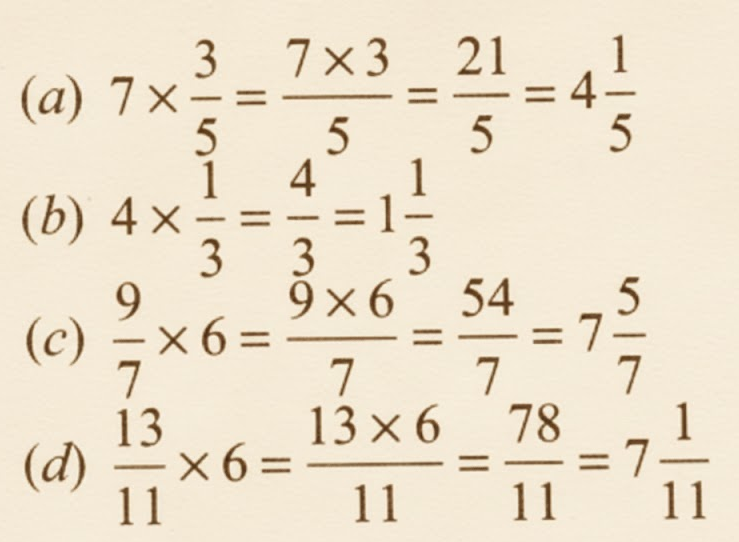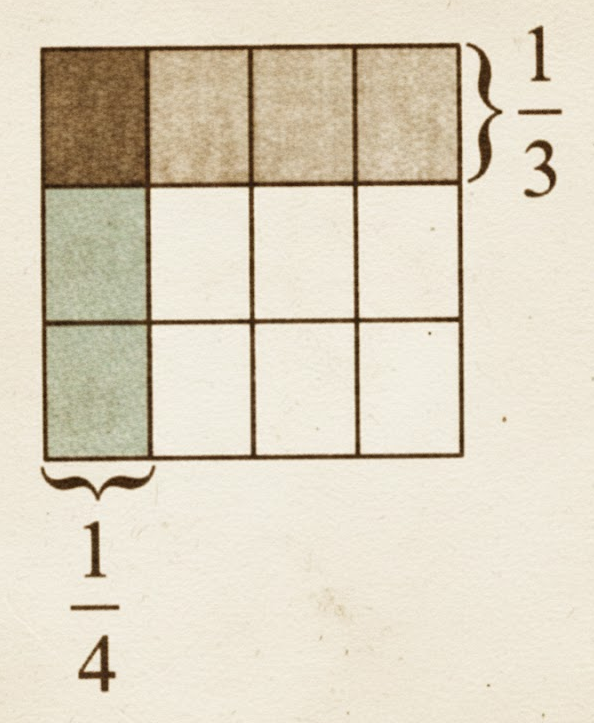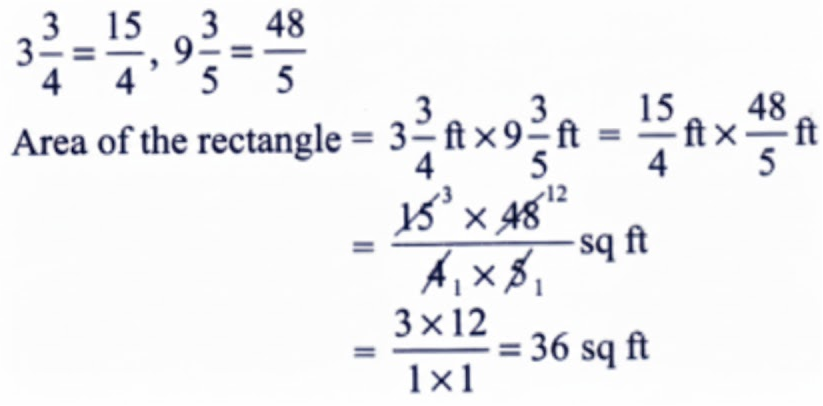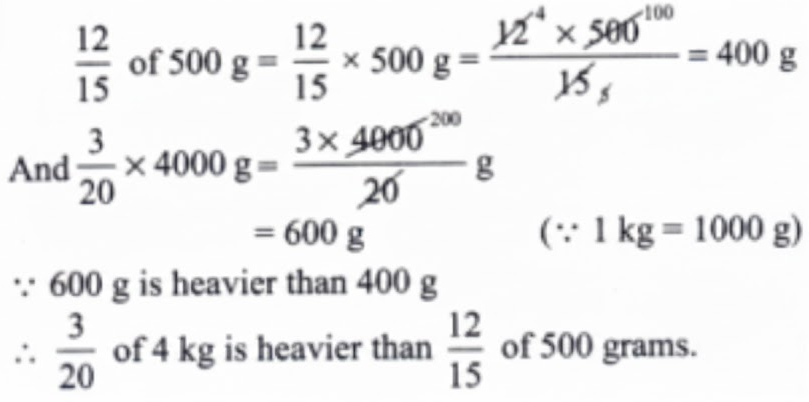How to Write Stepwise Answers for NCERT Class 7 Maths Chapter 8?
FAQs on NCERT Solutions For Class 7 Maths Chapter 8 Working with Fractions (2025-26)
1. What are the NCERT Solutions for Class 7 Maths Chapter 8 Working with Fractions?
NCERT Solutions for Class 7 Maths Chapter 8 Working with Fractions provide stepwise, syllabus-based answers to all textbook exercises so students can master fraction operations for exams. Key highlights include:
- Step-by-step solutions for all textbook and back exercises
- Clear explanations of addition, subtraction, multiplication, and division of fractions
- Aligned with CBSE 2025–26 marking scheme and syllabus
- Includes definitions, key formulae, and supporting diagrams where needed
2. How do I write stepwise answers for Class 7 Maths Chapter 8 to score full marks?
To score full marks in Class 7 Maths Chapter 8 Working with Fractions, present your answers using proper steps and align with CBSE expectations:
- Write the question clearly before starting
- Show every calculation or simplification step-by-step
- Highlight key formulae used (e.g., LCM for denominators, reciprocal rule for division)
- Box or underline the final answer for clarity
- Keep diagrams neat and label if required
- Follow the same method shown in NCERT Solutions
3. Which questions are likely to be asked from Working with Fractions in exams?
Important and likely exam questions from Chapter 8 Working with Fractions include:
- Simplify or solve given fraction expressions
- Solve word problems involving fractions (addition, subtraction, multiplication, division)
- Define key terms: proper, improper fractions, reciprocal
- Short answer: convert decimals to fractions and vice versa
- Application-based: real-life fraction usage
4. Are diagrams or definitions mandatory while answering Class 7 Maths Chapter 8 questions?
Definitions and diagrams are important in Class 7 Maths Chapter 8 as per marking scheme:
- Definitions: Always write clear definitions for terms like numerator, denominator, equivalent fractions when asked
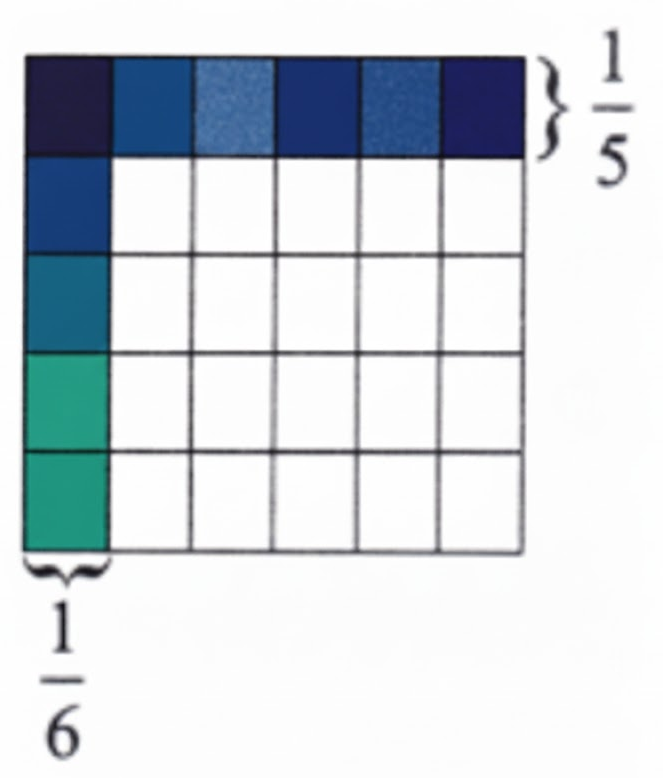
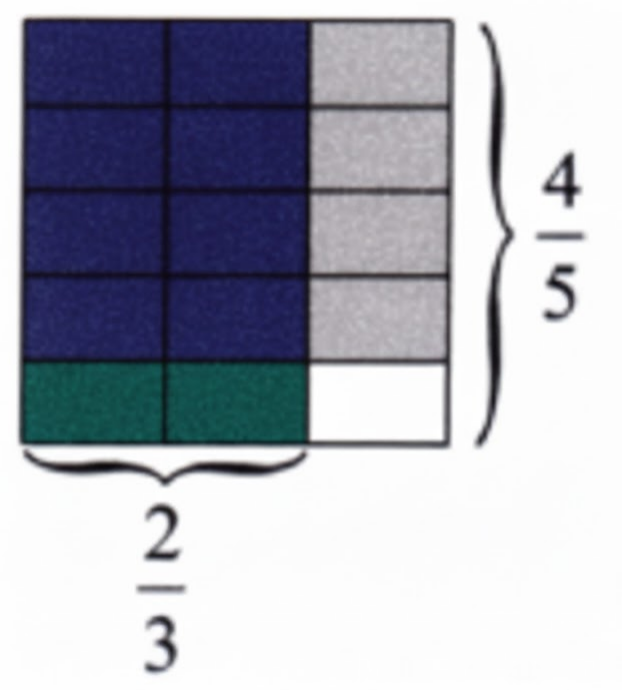
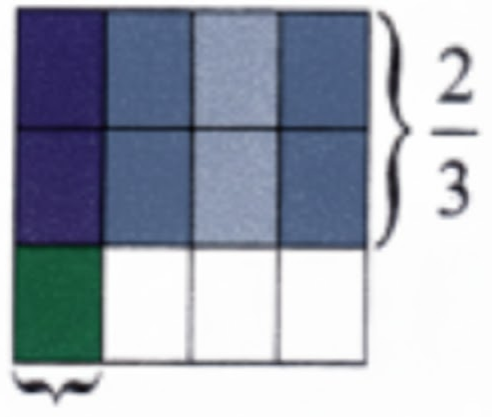
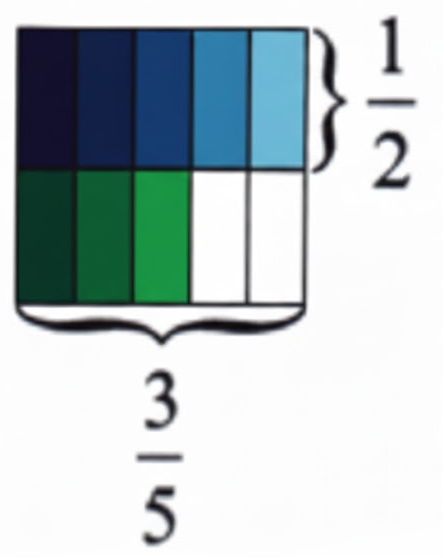
- Diagrams: Use visual fraction bars or circles where applicable, especially in explanatory questions
- If a question explicitly asks for a diagram or condition, you must include it for full marks
5. Where can I download the chapter’s solutions PDF for Class 7 Maths Chapter 8?
You can download the Class 7 Maths Chapter 8 NCERT Solutions PDF for offline revision from educational platforms.
- Look for a clearly marked 'Download PDF' button or link near the solutions
- Ensure the PDF covers all exercises and follows the latest CBSE 2025–26 syllabus
- PDFs are helpful for last-minute revision and offline access
6. How can I revise Class 7 Working with Fractions quickly before an exam?
For rapid revision of Class 7 Maths Chapter 8:
- Review stepwise NCERT Solutions with highlighted methods
- Revise key definitions and formulae (addition, subtraction, LCM, reciprocal)
- Attempt all exemplar and back exercise questions
- Solve at least one previous year/sample paper related to fractions
- Use flash notes or summary tables for quick recall
7. What are the main topics covered in Chapter 8 Working with Fractions Class 7 Maths?
Chapter 8 Working with Fractions (Class 7 Maths) covers:
- Types of fractions (proper, improper, mixed)
- Equivalent fractions and simplification
- Addition and subtraction of fractions
- Multiplication and division of fractions
- Word problems and real-life applications
8. Do examiners give partial marks for correct steps even if the final answer is wrong?
Yes, in CBSE Maths exams for Class 7, examiners often award partial marks for correct steps even if the final answer is incorrect, especially if:
- The calculation method and steps shown are accurate
- Errors are made only in the final arithmetic step
- All major steps according to NCERT solutions are attempted
9. How should I present long answers for Class 7 Maths fractions to match CBSE marking?
To match CBSE marking scheme for long answers in Working with Fractions:
- Start with a clear statement of method/definition
- Break calculations into small, logical steps with workings shown
- Highlight important numbers, results, and keywords
- Box the final answer; ensure the answer is labelled with units or terms if needed
- Keep presentation neat and avoid skipping steps
10. Are NCERT Solutions enough for Class 7 Maths exams?
NCERT Solutions are usually enough for Class 7 Maths exams because:
- They cover the entire syllabus as prescribed by CBSE
- Back exercise and exemplar questions often form the basis of exam papers
- Practising NCERT solutions ensures familiarity with all question types and marking scheme