NCERT Solutions for Class 7 Maths Chapter 9 Perimeter and Area

• Exercise 9.1: This exercise focuses on understanding the Perimeter. Calculation of the perimeter for different shapes such as rectangles, squares, and triangles.

• Exercise 9.2: This exercise focuses on understanding the Area of a Rectangle and Square. Calculation of the area of rectangles and squares.

Access NCERT Solutions for Class 7 Maths Chapter 9 – Perimeter and Area

Exercise – 9.1

1. Find the area of each of the following parallelograms:

a.

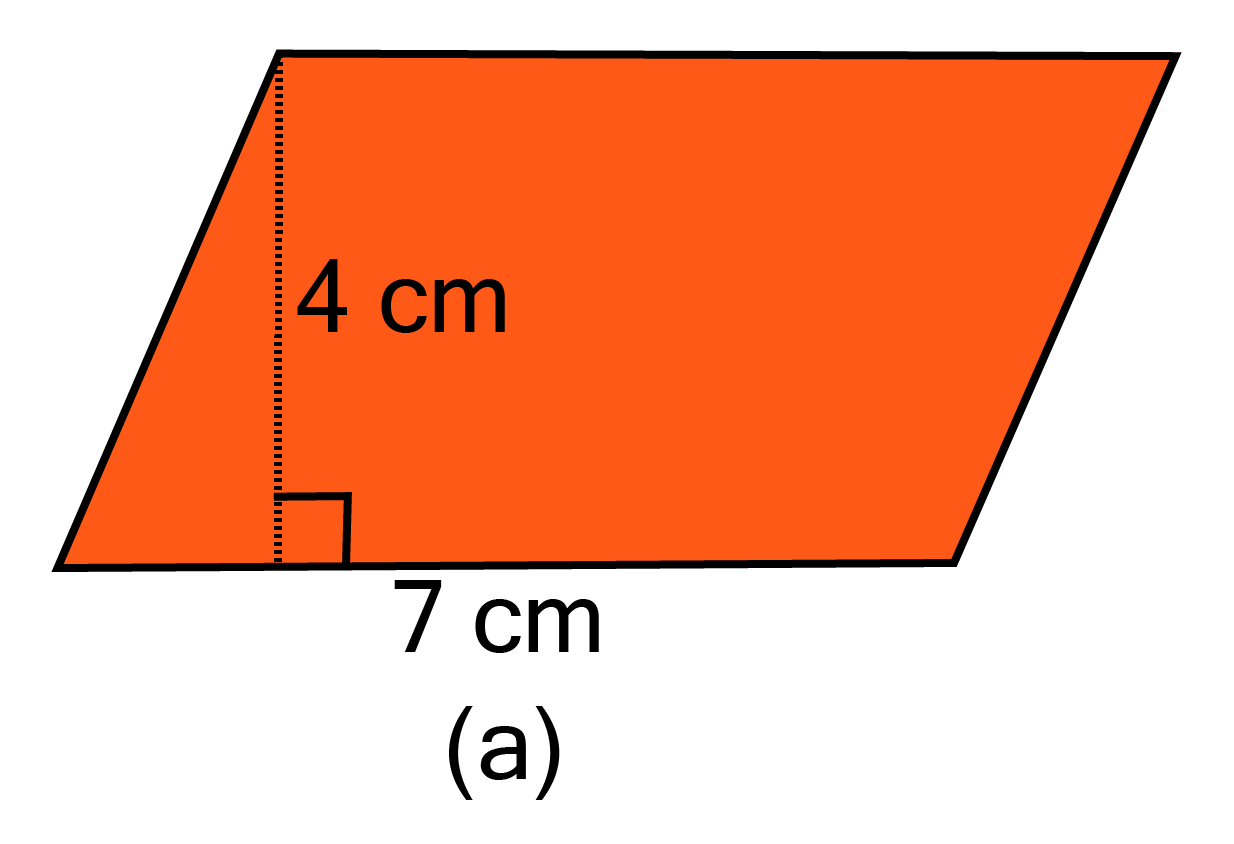
Ans: 

As the area of parallelogram ${\text{ =  base x height}}$ 

Given base ${\text{ =  7 cm}}$  and height ${\text{ =  4 cm}}$ 

$\therefore $ Area of parallelogram ${\text{ =  7 x 4  =  28 c}}{{\text{m}}^2}$ 

b.

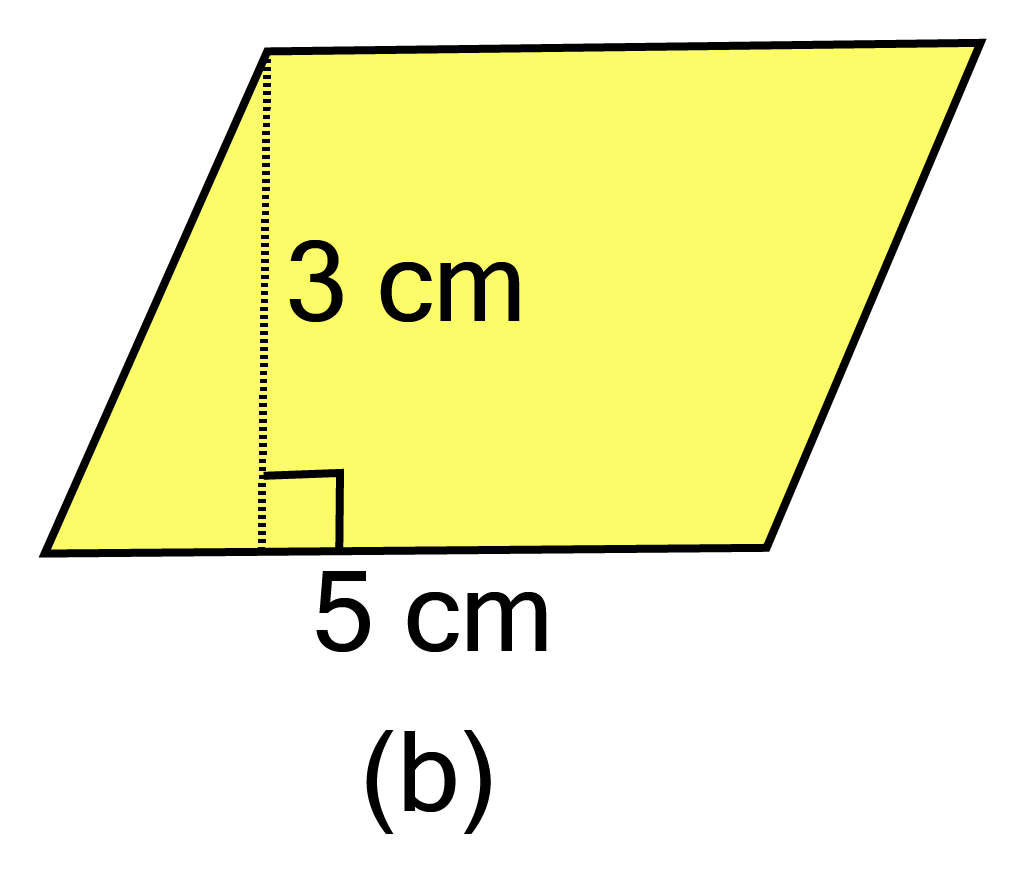
Ans:

Given base $ = {\text{ 5 cm}}$and height${\text{ =  3 cm}}$ 

$\therefore $ Area of parallelogram ${\text{ =  5 x 3  =  15 c}}{{\text{m}}^2}$ 

c.

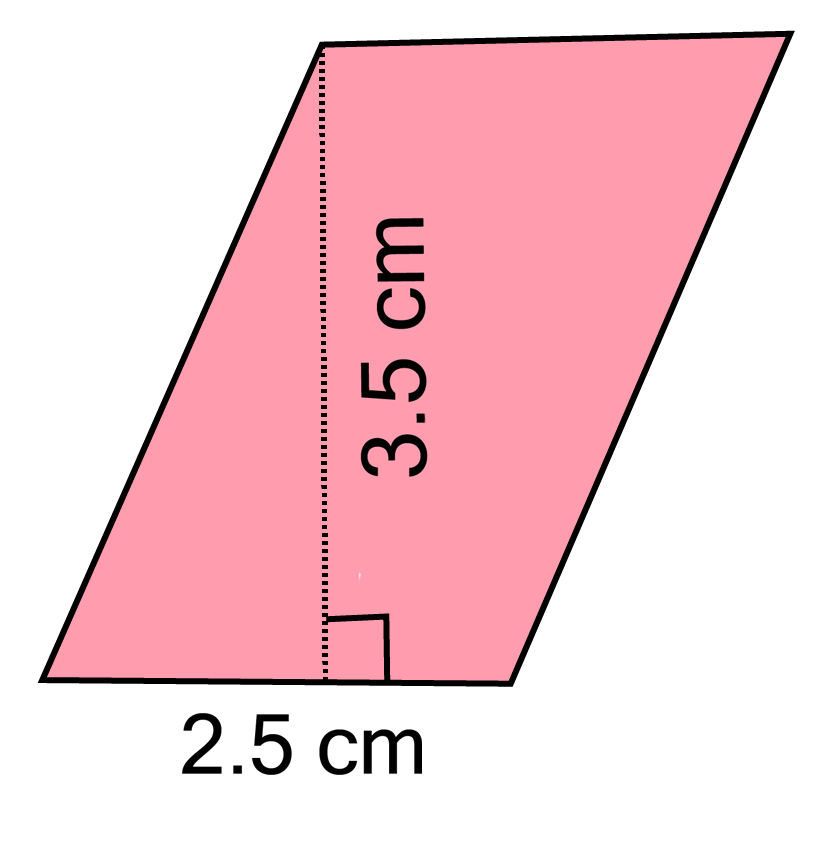
Ans: 

Given base ${\text{ =  2}}{\text{.5 cm}}$ and height ${\text{ =  3}}{\text{.5 cm}}$

$\therefore $ Area of parallelogram ${\text{ =  2}}{\text{.5 x 3}}{\text{.5  =  8}}{\text{.75 c}}{{\text{m}}^2}{\text{ }}$ 

d.

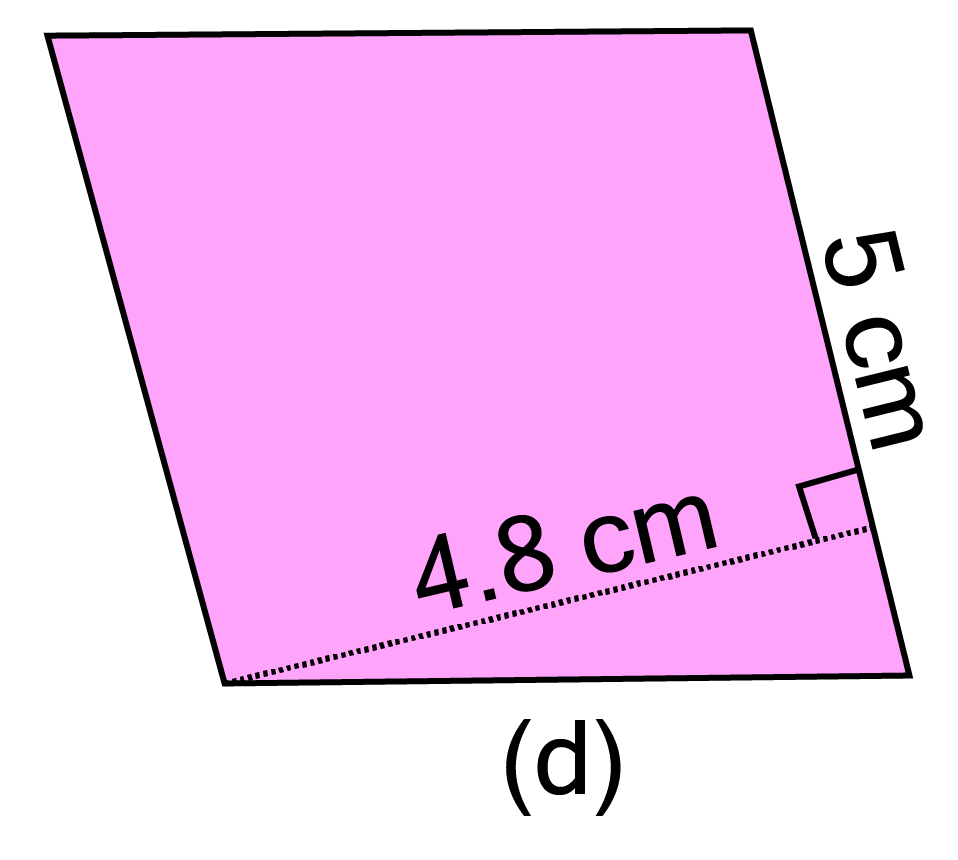
Ans: 

Given base ${\text{ =  5 cm}}$and height ${\text{ =  4}}{\text{.8 cm}}$ 

$\therefore $ Area of parallelogram ${\text{ =  5 x 4}}{\text{.8  =  24 c}}{{\text{m}}^2}$ 

e.

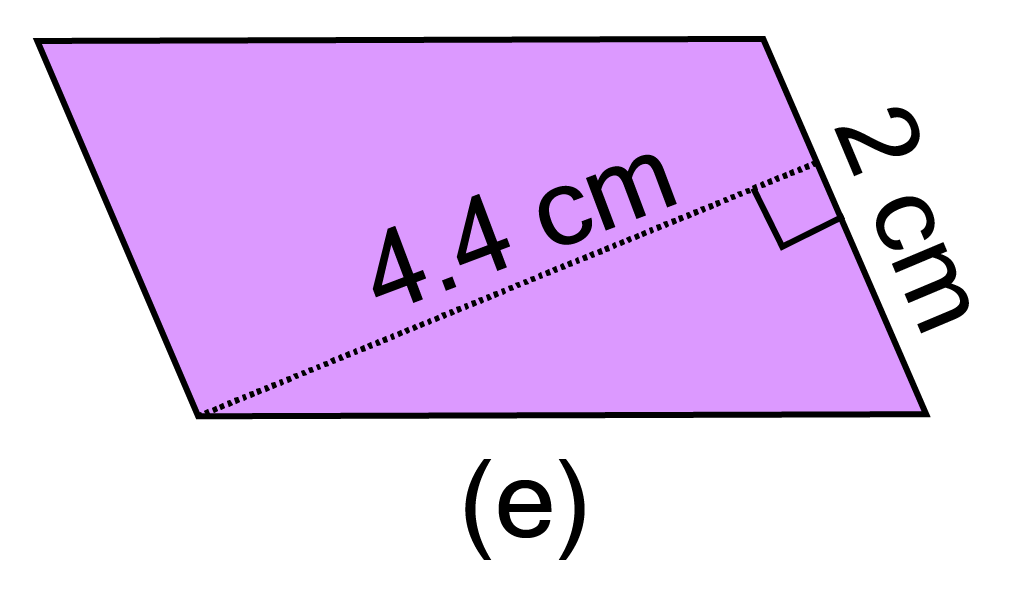
Ans: 

Given base ${\text{ =  2 cm}}$ and height ${\text{ =  4}}{\text{.4 cm}}$ 

$\therefore $ Area of parallelogram ${\text{ =  2 x 4}}{\text{.4  =  8}}{\text{.8 c}}{{\text{m}}^2}$  

2. Find the area of each of the following triangles:

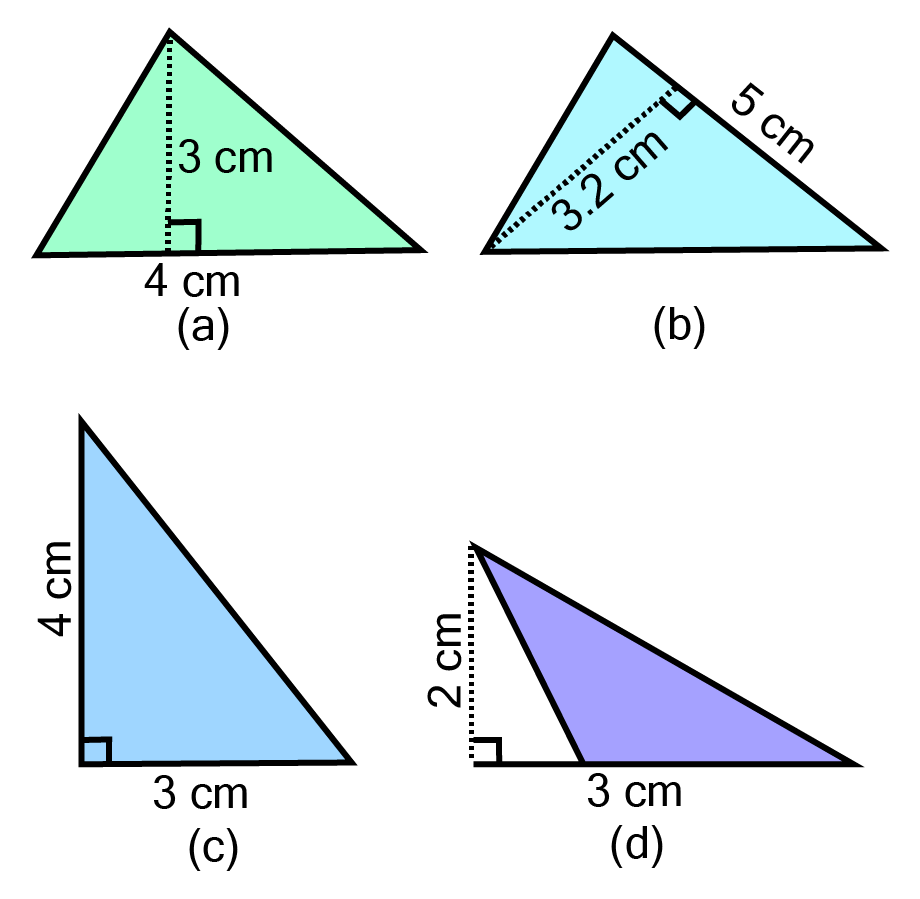
Ans:

As the area of triangle ${\text{ =  }}\dfrac{1}{2}{\text{ x base x height}}$ 

a. Given, base ${\text{ =  4 cm}}$ and height ${\text{ =  3 cm}}$ 

$\therefore $Area of triangle ${\text{ =  }}\dfrac{1}{2}{\text{ x 4 x 3  =  6 c}}{{\text{m}}^2}$ 

b. Given, base ${\text{ =  5 cm}}$ and height $ = {\text{ 3}}{\text{.2 cm}}$

$\therefore $ Area of triangle ${\text{ =  }}\dfrac{1}{2}{\text{ x 5 x 3}}{\text{.2  =  8 c}}{{\text{m}}^2}$ 

c. Given, base ${\text{ =  3 cm}}$ and height ${\text{ =  4 cm}}$ 

$\therefore $ Area of triangle ${\text{ =  }}\dfrac{1}{2}{\text{ x 3 x 4  =  6 c}}{{\text{m}}^2}$ 

d. Given, base ${\text{ =  3 cm}}$ and height ${\text{ =  2 cm}}$ 

$\therefore $ Area of triangle $ = {\text{ }}\dfrac{1}{2}{\text{ x  3 x 2  =  3 c}}{{\text{m}}^2}$ 

3. Find the missing values:

Ans:

As we know that, area of parallelogram ${\text{ =  base x height}}$

a. Here,  base ${\text{ =  20 cm}}$ and area ${\text{ =  246 c}}{{\text{m}}^2}$ 

$\Rightarrow 20{\text{ x height  =  246}} $

$\Rightarrow {\text{ height  =  }}\dfrac{{246}}{{20}} $

$\Rightarrow {\text{ height  =  12}}{\text{.3 cm}} $ 

b. Here, height $ = {\text{ 15 cm}}$ and area ${\text{ =  154}}{\text{.5 c}}{{\text{m}}^2}$ 

$\Rightarrow {\text{ base x 15  =  154}}{\text{.5}} $

$\Rightarrow {\text{ base  =  }}\dfrac{{154.5}}{{15}} $

$\Rightarrow {\text{ base  =  10}}{\text{.3 cm}} $ 

c. Here, height ${\text{ =  8}}{\text{.4 cm}}$ and area ${\text{ =  48}}{\text{.72 c}}{{\text{m}}^2}$ 

$\Rightarrow {\text{ base x 8}}{\text{.4  =  48}}{\text{.72}} $

$\Rightarrow {\text{ base  =  }}\dfrac{{48.72}}{{8.4}} $

$\Rightarrow {\text{ base  =  5}}{\text{.8 cm}} $   

d. Here, base ${\text{ =  15}}{\text{.6 cm}}$ and area $ = {\text{ 16}}{\text{.38 c}}{{\text{m}}^2}$ 

$\Rightarrow {\text{ 15}}{\text{.6 x height  =  16}}{\text{.38}} $

$\Rightarrow {\text{ height  =  }}\dfrac{{16.38}}{{15.6}} $

$\Rightarrow {\text{ height  =  1}}{\text{.05 cm}} $ 

Hence, the missing values are:

4. Find the missing values:

Ans:

As the area of triangle ${\text{ =  }}\dfrac{1}{2}{\text{ x base x height}}$ 

a. Given, base ${\text{ =  15 cm}}$ and area ${\text{ =  87 c}}{{\text{m}}^2}$ 

$\Rightarrow {\text{ }}\dfrac{1}{2}{\text{ x 15 x height  =  87}} $

$\Rightarrow {\text{ height  =  }}\dfrac{{87{\text{ x 2}}}}{{15}} $

$\Rightarrow {\text{ height  =  11}}{\text{.6 cm}} $ 

b. Given, height ${\text{ =  31}}{\text{.4 mm}}$ and area ${\text{ =  1256 m}}{{\text{m}}^2}$ 

$\Rightarrow {\text{ }}\dfrac{1}{2}{\text{ x base x 31}}{\text{.44  =  1256}} $

$\Rightarrow {\text{ base  =  }}\dfrac{{1256{\text{ x 2}}}}{{31.44}} $

$\Rightarrow {\text{ base  =  80 mm}} $ 

c. Given, base ${\text{ =  22 cm}}$ and area $ = {\text{ 170}}{\text{.5 c}}{{\text{m}}^2}$ 

$\Rightarrow {\text{ }}\dfrac{1}{2}{\text{ x 22 x height  =  170}}{\text{.5}} $

$\Rightarrow {\text{ height  =  }}\dfrac{{170.5{\text{ x 2}}}}{{22}} $

$\Rightarrow {\text{ height  =  15}}{\text{.5 cm}} $

Hence, the missing values are:

5. PQRS is a parallelogram. QM is the height from Q to SR and QN is the height from Q to PS. If SR ${\text{ =  12 cm}}$ and QM ${\text{ =  7}}{\text{.6 cm}}$.

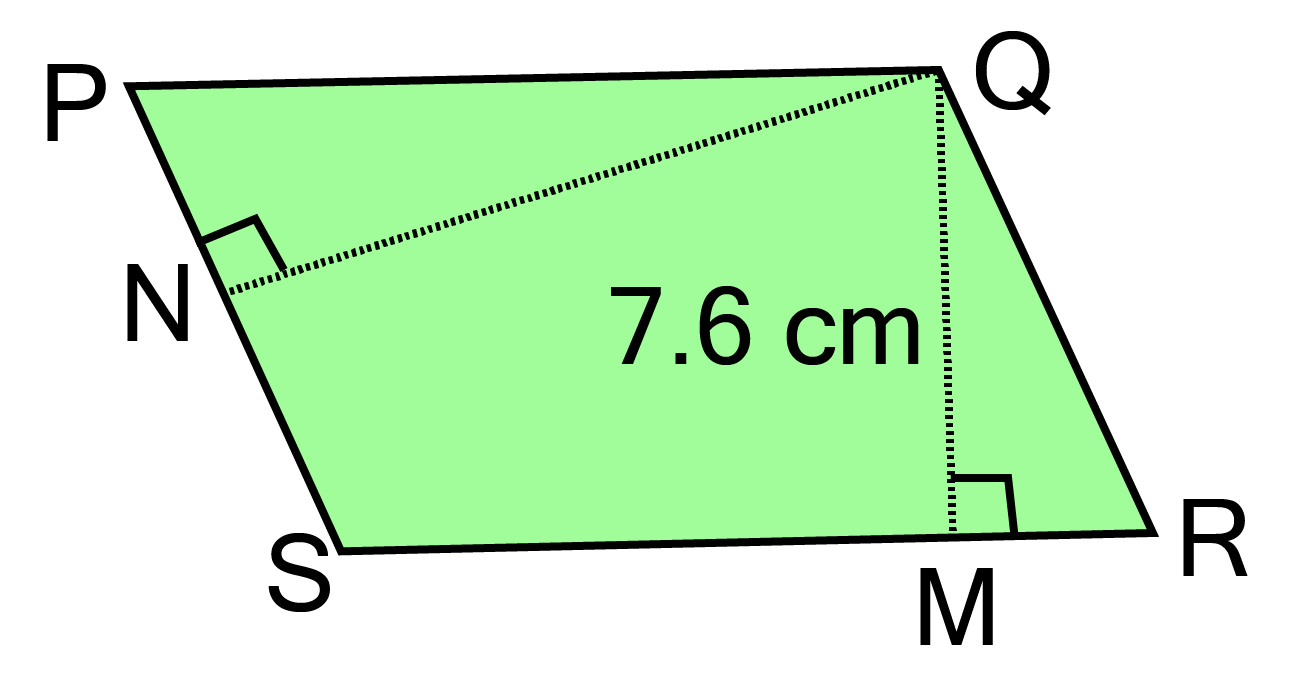
Find:  a. the area of the parallelogram PQRS 

Ans:

In given parallelogram PQRS, 

SR ${\text{ =  12 cm}}$, QM $ = {\text{ 7}}{\text{.6 cm}}$ , PS ${\text{ =  8 cm}}$ 

Area of parallelogram ${\text{ =  base x height  =  12 x 7}}{\text{.6  =  91}}{\text{.2 c}}{{\text{m}}^2}{\text{ }}$

b. QN, if PS ${\text{ =  8 cm}}$

Ans: Area of parallelogram ${\text{ =  base x height}}$ 

$\Rightarrow {\text{ 91}}{\text{.2  =  8 x QN}} $

$\Rightarrow {\text{ QN  =  }}\dfrac{{91.2}}{8} $

$\Rightarrow {\text{ QN  =  11}}{\text{.4 cm}} $

6. DL and BM are the heights on sides AB and AD respectively of parallelogram ABCD. If the area of the parallelogram is $1470{\text{ c}}{{\text{m}}^2}$, AB $ = {\text{ 35 cm}}$ and AD $ = {\text{ 49 cm}}$ , find the length of BM and DL.

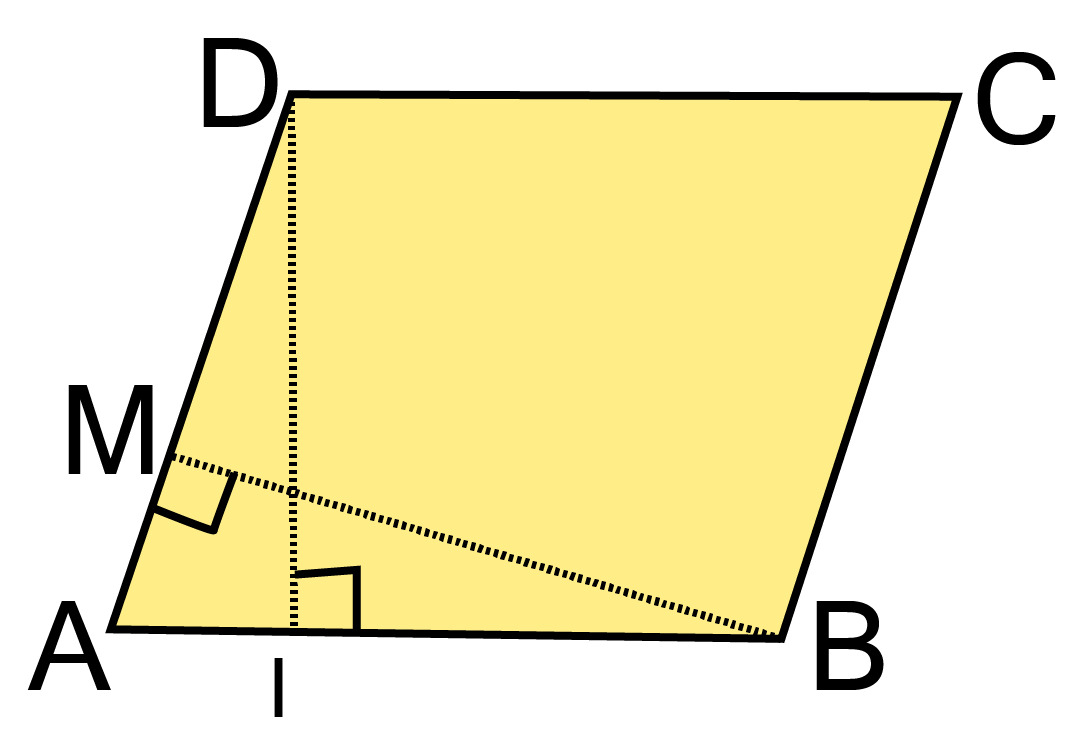
Ans:

In the given parallelogram ABCD,

Area of parallelogram ${\text{ =  1470 c}}{{\text{m}}^2}$ 

Base (AB) ${\text{ =  35 cm}}$ 

Base (AD) $ = {\text{ 49 cm}}$ 

$\because $ area of parallelogram $ = {\text{ base x height}}$ 

$\Rightarrow {\text{ 1470  =  35 x DL}} $

$\Rightarrow {\text{ DL  =  }}\dfrac{{1470}}{{35}} $

$\Rightarrow {\text{ DL  =  42 cm}} $ 

Also,

$\Rightarrow {\text{ 1470  =  49 x BM}} $

$\Rightarrow {\text{ BM  =  }}\dfrac{{1470}}{{49}} $

$\Rightarrow {\text{ BM  =  30 cm}} $ 

Thus, the lengths of DL and BM are 42 cm and 30 cm respectively.

7. ∆ ABC is right angled at A. AD is perpendicular to BC. If AB $ = {\text{ 5 cm}}$ , BC ${\text{ =  13 cm}}$  and AC $ = {\text{ 12 cm}}$, find the area of ∆ ABC. Also, find the length of AD.

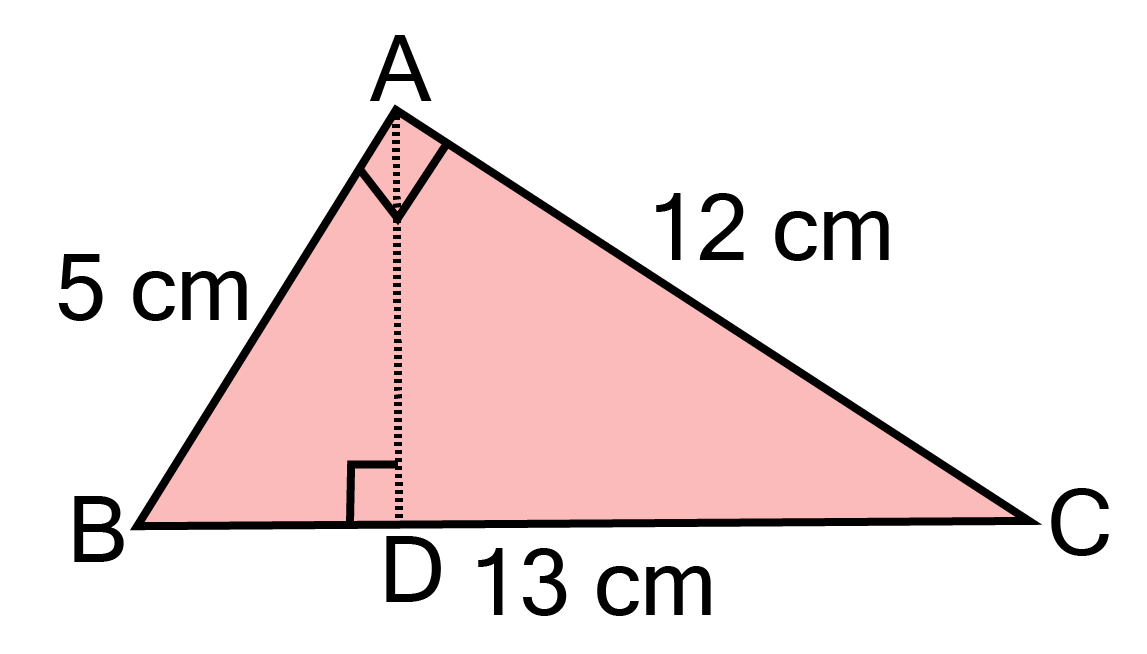
Ans:

In right angled triangle BAC,

AB $ = {\text{ 5 cm}}$ and AC $ = {\text{ 12 cm}}$ 

We know that, area of triangle ${\text{ =  }}\dfrac{1}{2}{\text{x base x height}}$ 

$\Rightarrow $ Area of triangle ${\text{ =  }}\dfrac{1}{2}{\text{ x AB x AC  =  }}\dfrac{1}{2}{\text{ x 5 x 12  =  30 c}}{{\text{m}}^2}$ 

Now, in triangle ABC,

Area of triangle ABC $ = {\text{ }}\dfrac{1}{2}{\text{ x BC x AD}}$

$\Rightarrow {\text{ 30  =  }}\dfrac{1}{2}{\text{ x 13 x AD}} $

$\Rightarrow {\text{ AD  =  }}\dfrac{{30{\text{ x 2}}}}{{13}} $

$\Rightarrow {\text{ AD  =  }}\dfrac{{60}}{{13}}{\text{ cm}} $ 

8. ∆ ABC is isosceles with ${\text{AB  =  AC  =  7}}{\text{.5 cm}}$and BC $ = {\text{ 9 cm}}$. The height AD from A to BC, is  ${\text{6 cm}}$. Find the area of ∆ ABC. What will be the height from C to AB i.e., CE?

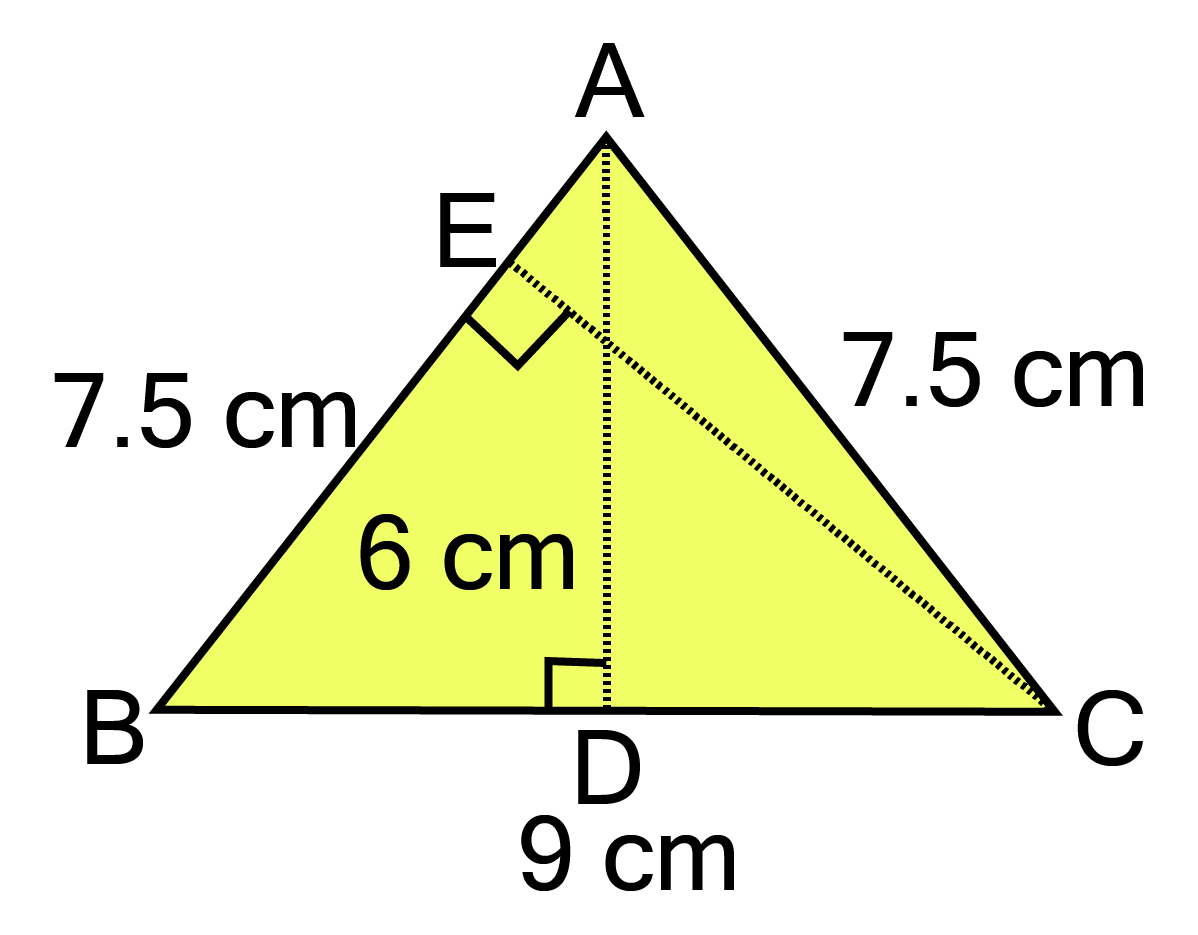
Ans:

in given triangle ABC,

AD $ = {\text{ 6 cm}}$ and BC ${\text{ =  9 cm}}$ 

We know that, area of triangle $ = {\text{ }}\dfrac{1}{2}{\text{ x base x height}}$ 

$ \Rightarrow $  area of triangle $ = {\text{ }}\dfrac{1}{2}{\text{ x BC x AD  =  }}\dfrac{1}{2}{\text{ x 9 x 6  =  27 c}}{{\text{m}}^2}$ 

Also,

area of triangle $ = {\text{ }}\dfrac{1}{2}{\text{ x base x height}}$

$\Rightarrow {\text{ 27  =  }}\dfrac{1}{2}{\text{ x AB x CE}} $

$\Rightarrow {\text{ 27  =  }}\dfrac{1}{2}{\text{ x 7}}{\text{.5 x CE}} $

$\Rightarrow {\text{ CE  =  }}\dfrac{{27{\text{ x 2}}}}{{7.5}} $

$\Rightarrow {\text{ CE  =  7}}{\text{.2 cm}} $ 

Thus, the height from C to AB i.e., CE is  ${\text{7}}{\text{.2 cm}}$.

Exercise – 9.2

1. Find the circumference of the circles with the following radius: (take  $\pi = \dfrac{{{\text{22}}}}{{\text{7}}}$ )

a. 14 cm

Ans:

We know that, circumference of circle  =  2 $\pi r$ 

$\therefore $ Circumference of the given circle ${\text{ =  2 x }}\dfrac{{22}}{7}{\text{ x 14  =  88 cm}}$ 

b. 28 mm

Ans:

We know that, circumference of circle =  2 $\pi r$

$\therefore $ Circumference of the given circle ${\text{ =  2 x }}\dfrac{{22}}{7}{\text{ x 28  =  176 mm}}$ 

c. 21 cm

Ans:

We know that, circumference of circle 2 $\pi r$

$\therefore $ Circumference of the given circle ${\text{ =  2 x }}\dfrac{{22}}{7}{\text{ x 21  =  132 cm}}$

2. Find the area of the following circles, given that: (take  $\pi = \dfrac{{{\text{22}}}}{{\text{7}}}$ )

a. radius $ = {\text{ 14 mm}}$ 

Ans:

We know that, area of circle $ =  \pi {{\text{r}}^{\text{2}}}$ 

Given, radius $ = {\text{ 14 mm}}$ 

$\therefore $  area of circle ${\text{ =  }}\dfrac{{22}}{7}{\text{ x 14 x 14  =  616 m}}{{\text{m}}^2}$ 

b. diameter ${\text{ =  49 m}}$

Ans:

We know that, area of circle $ =  \pi {{\text{r}}^{\text{2}}}$

Given, diameter ${\text{ =  49 m}}$ 

$\because {\text{ radius  =  }}\dfrac{{{\text{diameter}}}}{2}{\text{  =  }}\dfrac{{49}}{2}{\text{ m}}$ 

$\therefore $  area of circle ${\text{ =  }}\dfrac{{22}}{7}{\text{ x }}\dfrac{{49}}{2}{\text{ x }}\dfrac{{49}}{2}{\text{  =  1886}}{\text{.5 }}{{\text{m}}^2}$

c. radius ${\text{ =  5 cm}}$

Ans:

We know that, area of circle $ =  \pi {{\text{r}}^{\text{2}}}$

Given, radius ${\text{ =  5 cm}}$ 

$\therefore $  area of circle ${\text{ =  }}\dfrac{{22}}{7}{\text{ x 5 x 5  =  }}\dfrac{{550}}{7}{\text{ c}}{{\text{m}}^2}$

3. If the circumference of a circular sheet is  $154{\text{ m}}$ , find its radius. Also find the area of the sheet. (take  $\pi = \dfrac{{{\text{22}}}}{{\text{7}}}$ )

Ans:

Given, circumference of the circular sheet ${\text{ =  154 m}}$

$\Rightarrow 2 \pi {\text{r}} =  154 $

$\Rightarrow {\text{ 2 x }}\dfrac{{22}}{7}{\text{ x r  =  154}} $

$\Rightarrow {\text{ r  =  }}\dfrac{{154{\text{ x 7}}}}{{2{\text{ x 22}}}} $

$\Rightarrow {\text{ r  =  24}}{\text{.5 m}} $

Now, area of circular sheet $ =  \pi {{\text{r}}^{\text{2}}}{\text{  =  }}\dfrac{{{\text{22}}}}{{\text{7}}}{\text{ x 24}}{\text{.5 x 24}}{\text{.5  =  1886}}{\text{.5 }}{{\text{m}}^{\text{2}}}$

Thus, the radius and area of the circular sheet are $24.5{\text{ m}}$ and $1886.5{\text{ }}{{\text{m}}^2}$ respectively.

4. A gardener wants to fence a circular garden of diameter $21{\text{ m}}$ . Find the length of the rope he needs to purchase, if he makes 2 rounds of fence. Also, find the costs of the rope, if it costs  ₹$4$ per meter. (take  $\pi = \dfrac{{{\text{22}}}}{{\text{7}}}$ )

Ans:

Given, diameter of the circular garden $ = {\text{ 21 m}}$ 

$\therefore $ radius of circular garden $ = {\text{ }}\dfrac{{21}}{2}{\text{ m}}$ 

Now, circumference of the circular garden =2 $\pi r$

$\therefore $ circumference of the circular garden $ = {\text{ 2 x }}\dfrac{{22}}{7}{\text{ x }}\dfrac{{21}}{2}{\text{  =  66 m}}$ 

The gardener makes 2 rounds of fence,

So, the total length of the rope of fencing = 2 $\pi r  =  2 x 66  =  132 m$

$\because $  the cost of $1{\text{ m}}$ rope $ = $ ₹ $4$ 

$\therefore $  the cost of $132{\text{ m}}$ rope $ = $ $4{\text{ x 132  = }}$ ₹$528$ 

5. From a circular sheet of radius $4{\text{ cm}}$ , a circle of radius ${\text{3 cm}}$ is removed. Find the area of the remaining sheet. (Take $\pi {\text{  =  3}}{\text{.14}}$) 

Ans:

Given, radius of circular sheet(R) $ = {\text{ 4 cm}}$ 

Radius of removed circle(r) $ = {\text{ 3 cm}}$

$\therefore $ area of remaining sheet $ = $ area of circular sheet $ - $ area of removed circle

$\therefore $ area of remaining sheet $=\pi R^{2}-\pi r^{2}$ 

$\therefore $ area of remaining sheet ${\text{ =  (3}}{\text{.14 x 4 x 4)   -  (3}}{\text{.14 x 3 x 3)}}$ 

$\therefore $ area of remaining sheet ${\text{ =  3}}{\text{.14 x (16  -  9)  =  3}}{\text{.14 x 7  =  21}}{\text{.98 c}}{{\text{m}}^2}$

Thus, the area of the remaining sheet is $21.98{\text{ c}}{{\text{m}}^2}$ .

6. Saima wants to put a lace on the edge of a circular table cover of diameter ${\text{1}}{\text{.5 m}}$. Find the length of the lace required and also find its cost if one meter of the lace costs ` ₹$15$. (Take $\pi {\text{  =  3}}{\text{.14}}$)

Ans:

Given, diameter of the circular table cover $ = {\text{ 1}}{\text{.5 m}}$ 

$\therefore $ radius of the circular table $ = {\text{ }}\dfrac{{1.5}}{2}{\text{ m}}$

Now, circumference of the circular table ${\text{ =  2}}\pi {\text{r  =  2 x 3}}{\text{.14 x }}\dfrac{{1.5}}{2}{\text{  =  4}}{\text{.71 m}}$ 

$\therefore $ the length of required lace is $4.71{\text{ m}}$ 

As, the cost of $1{\text{ m}}$ lace = ₹$15$

The cost of $4.71{\text{ m}}$lace $ = {\text{ 4 x 4}}{\text{.71  =  }}$ ₹$70.65$ 

Hence, the cost of $4.71{\text{ m}}$is ₹$70.65$.

7. Find the perimeter of the adjoining figure, which is a semicircle including its diameter. 

Ans:

Given, diameter $ = {\text{ 10 cm}}$ 

$\therefore {\text{ radius  =  }}\dfrac{{{\text{diameter}}}}{2}{\text{  =  }}\dfrac{{10}}{2}{\text{  =  5 cm}}$ 

As per the question,

Perimeter of the figure $ = $ circumference of semicircle $ + $ diameter

$\therefore $ perimeter of the figure  $\pi r$  +  $d  =  \dfrac{{22}}{7}{\text{ x 5  +  10 }}$ 

$\therefore $ perimeter of the figure ${\text{ =  }}\dfrac{{110}}{7}{\text{  +  10  =  }}\dfrac{{110 + 70}}{7}{\text{  =  }}\dfrac{{180}}{7}{\text{  =  25}}{\text{.71 cm}}$ 

Hence, the perimeter of the given figure is $25.71{\text{ cm}}$ 

8. Find the cost of polishing a circular table-top of diameter $1.6{\text{ m}}$ , if the rate of polishing is ₹$15{\text{/}}{{\text{m}}^2}$ . (Take $\pi {\text{  =  3}}{\text{.14}}$)

Ans:

Given, diameter of the circular table top $ = {\text{ 1}}{\text{.6 m}}$ 

$\therefore $ radius of the circular table top $ = {\text{ }}\dfrac{{1.6}}{2}{\text{  =  0}}{\text{.8 m}}$ 

Now, area of the circular table top $ =  \pi {{\text{r}}^{\text{2}}}{\text{  =  3}}{\text{.14 x 0}}{\text{.8 x 0}}{\text{.8  =  2}}{\text{.0096 }}{{\text{m}}^2}$ 

The cost of $1{\text{ }}{{\text{m}}^2}$ of polishing $ = $ ₹$15$ 

$\therefore $ the cost of $2.0096{\text{ }}{{\text{m}}^2}$ of polishing ${\text{ =  15 x 2}}{\text{.0096  =  30}}{\text{.14(approx)}}$ 

Hence the cost of polishing a circular table of $2.0096{\text{ }}{{\text{m}}^2}$is ₹$30.14$ (approx).

9. Shazli took a wire of length $44{\text{ cm}}$  and bent it into the shape of a circle. Find the radius of that circle. Also find its area. If the same wire is bent into the shape of a square, what will be the length of each of its sides? Which figure encloses more area, the circle or the square? (take  $\pi = \dfrac{{{\text{22}}}}{{\text{7}}}$ )

Ans:

Given, total length of the wire $ = {\text{ 44 cm}}$ 

$\therefore $ circumference of the circle =2 $\pi r$ 

$\Rightarrow { 2\pi r  =  44} $

$\Rightarrow {\text{ 2 x }}\dfrac{{{\text{22}}}}{{\text{7}}}{\text{ x r  =  44}} $

$\Rightarrow {\text{ r  =  }}\dfrac{{{\text{44 x 7}}}}{{{\text{2 x 22}}}} $

$\Rightarrow {\text{r =  7 cm}} $ 

Now, area of circle $ =  \pi {{\text{r}}^{\text{2}}}{\text{  =  }}\dfrac{{22}}{7}{\text{ x 7 x 7  =  154 c}}{{\text{m}}^2}$ 

Now, the wire is converted into square

$\therefore $ the perimeter of square $ = {\text{ 44 cm}}$ 

$\Rightarrow {\text{ 4 x side  =  44}} $

$\Rightarrow {\text{ side  =  }}\dfrac{{44}}{4}{\text{  =  11 cm}} $ 

So, the area of square $ = $ side ${\text{x}}$ side $ = $ $11{\text{ x 11  =  121 c}}{{\text{m}}^2}$ 

Therefore, in comparison, the area of a circle is greater than that of a square, so the circle encloses more area.

10. From a circular card sheet of radius $14{\text{ cm}}$ , two circles of radius $3.5{\text{ cm}}$  and a rectangle of length $3{\text{ cm}}$and breadth ${\text{1 cm}}$are removed (as shown in the adjoining figure). Find the area of the remaining sheet. (take  $\pi = \dfrac{{{\text{22}}}}{{\text{7}}}$ )

Ans:

Given, radius of circular sheet(R) $ = {\text{ 14 cm}}$ 

Radius of smaller circle(r) $ = {\text{ 3}}{\text{.5 cm}}$

Length of rectangle (l) $ = {\text{ 3 cm}}$

Breadth of the rectangle (b) $ = {\text{ 1 cm}}$

As per given,

Area of remaining sheet $ = $ area of circular sheet $ - $ (area of two smaller circle $ + $ area of rectangle)

$=x R^{2}-\left[2\left(\pi r^{2}\right)+(l \times b)\right]$

$= {\text{ [}}\dfrac{{22}}{7}{\text{ x 14 x 14]  -  [(2 x }}\dfrac{{22}}{7}{\text{ x 3}}{\text{.5 x 3}}{\text{.5)  +  (3 x 1)]}} $

${\text{ =  [22 x 14 x 2]  -  [(44 x 0}}{\text{.5 x 3}}{\text{.5)  +  3]}} $

${\text{ =  616  -  80}} $

${\text{ =  536 c}}{{\text{m}}^2} $

Hence, the area of the remaining sheet is $536{\text{ c}}{{\text{m}}^2}$ 

11. A circle of radius ${\text{2 cm}}$  is cut out from a square piece of an aluminium sheet of side $6{\text{ cm}}$. What is the area of the leftover aluminium sheet? (Take $\pi {\text{  =  3}}{\text{.14}}$)

Ans:

Given, radius of circle $ = {\text{ 2 cm}}$ 

Side of aluminium square sheet $ = {\text{ 6 cm}}$

As per given,

Area of aluminium sheet left $ = $ total area of square sheet $ - $ area of circle

$=$ side x side $-\pi r^{2}$

${\text{ =  (6 x 6)  -  (3}}{\text{.14 x 2 x 2)}} $

${\text{ =  36  -  12}}{\text{.56  =  23}}{\text{.44 c}}{{\text{m}}^2} $ 

Hence, the area of aluminium sheet left is $23.44{\text{ c}}{{\text{m}}^2}$

12. The circumference of a circle is${\text{31}}{\text{.4 cm}}$. Find the radius and the area of the circle. (Take $\pi {\text{  =  3}}{\text{.14}}$)

Ans:

Given, the circumference of the circle $ = {\text{ 31}}{\text{.4 cm}}$ 

$\Rightarrow 2\pi r  =  31{\text{.4}} $

$\Rightarrow {\text{ 2 x 3}}{\text{.14 x r  =  31}}{\text{.4}} $

$\Rightarrow {\text{ r  =  }}\dfrac{{31.4}}{{2{\text{ x 3}}{\text{.14}}}} $

$\Rightarrow {\text{ r  =  5 cm}} $ 

Now, area of circle $=\pi r^{2}=3.14 \times 5 \times 5$  $=78.5 \mathrm{~cm}^{2}$

Therefore, the radius and area of the circle are $5{\text{ cm}}$ and $78.5{\text{ c}}{{\text{m}}^2}$ respectively.

13. A circular flower bed is surrounded by a path $4{\text{ m}}$  wide. The diameter of the flower bed is ${\text{66 m}}$. What is the area of this path? (Take $\pi {\text{  =  3}}{\text{.14}}$)

Ans:

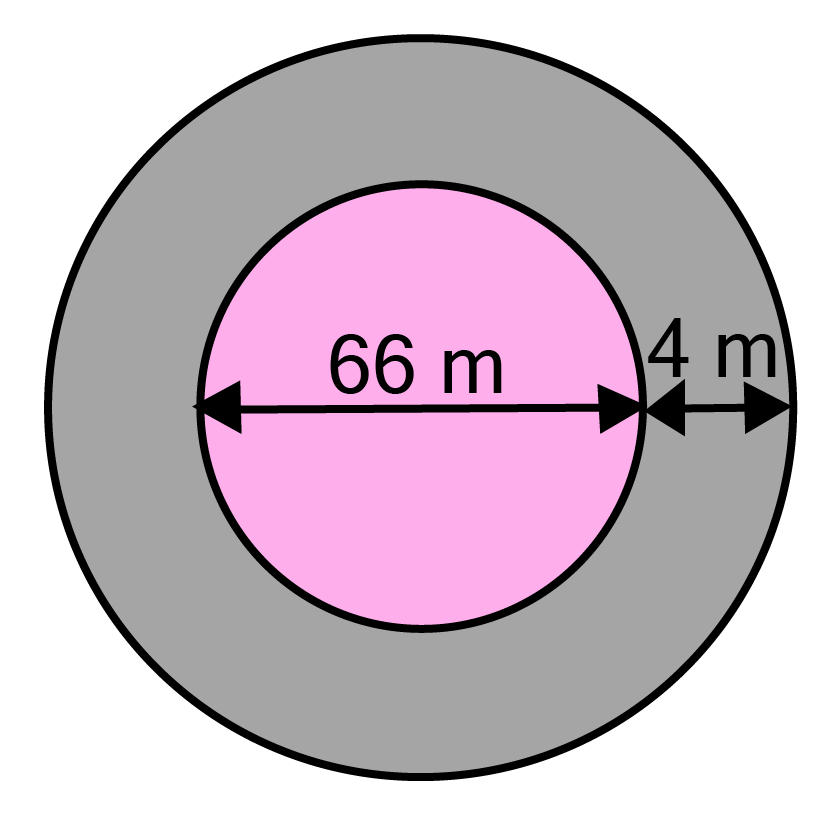
Given, diameter of the circular flower bed $ = {\text{ 66 m}}$ 

$\therefore $ radius of circular flower bed(r) $ = \dfrac{{66}}{2}{\text{  =  33 m}}$ 

$\therefore $ radius of circular flower bed with $4{\text{ m}}$ wide path(R) $ = {\text{ 33  +  4  =  37 m}}$ 

As per given,

Area of path $ = $ area of bigger circle $ - $ area of smaller circle

$=\pi \mathrm{R}^{\mathrm{2}}-\pi r^{2}=\pi\left({R}^{2}-r^{2}\right)$ 

\[{\text{ =  [(37}}{{\text{)}}^2}{\text{  -  (33}}{{\text{)}}^2}{\text{]}}\]

$= {\text{ 3}}{\text{.14[(37  +  33)(37  -  33)]}} $

${\text{ =  3}}{\text{.14 x 7 x 4  =  879}}{\text{.20 }}{{\text{m}}^2} $ 

$[\because {\text{ }}{{\text{a}}^2} - {\text{ }}{{\text{b}}^2}{\text{  =  (a  +  b)(a  -  b)]}}$ 

Hence, the area of the path is $879.20{\text{ }}{{\text{m}}^2}$ 

14. A circular flower garden has an area of $314{\text{ }}{{\text{m}}^2}$ . A sprinkler at the centre of the garden can cover an area that has a radius of $12{\text{ m}}$. Will the sprinkler water the entire garden?  (Take $\pi {\text{  =  3}}{\text{.14}}$)

Ans:

We know that, circumference of the circle =  2 $\pi r$ 

Circular area by the sprinkler $ = {\text{ 3}}{\text{.14 x 12 x 12  =  3}}{\text{.14 x 144  =  452}}{\text{.16 }}{{\text{m}}^2}$ 

Given, area of the circular flower garden $ = {\text{ 314 }}{{\text{m}}^2}$ 

As the area of the circular flower garden is smaller than the area by sprinkler, hence sprinkler will water the entire garden. 

15. Find the circumference of the inner and the outer circles, shown in the adjoining figure.  (Take $\pi {\text{  =  3}}{\text{.14}}$)

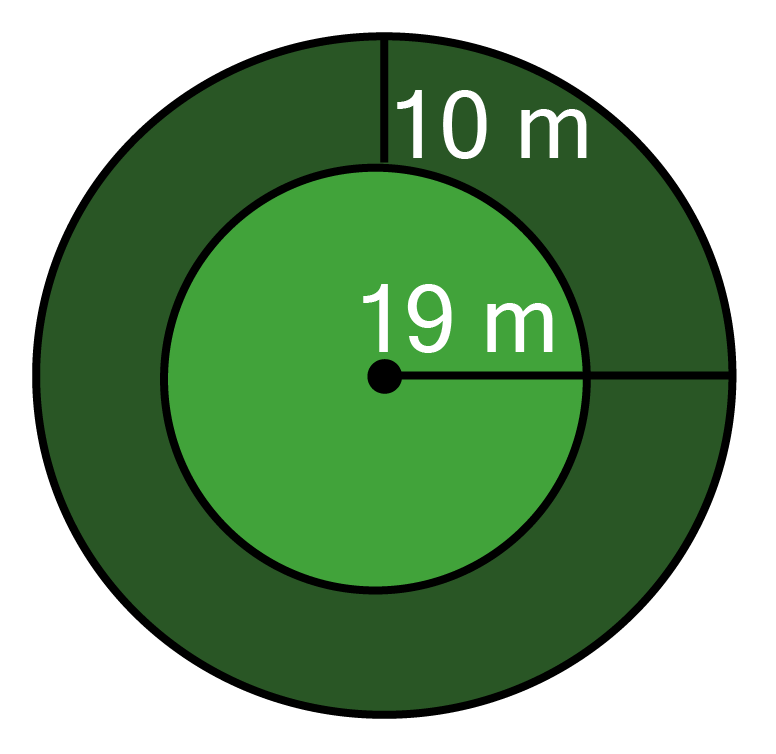
Ans:

given, radius of outer circle(r) $ = {\text{ 19 m}}$ 

$\therefore $ circumference of outer circle =  2 $\pi r$ $ = {\text{ 2 x 3}}{\text{.14 x 19  =  119}}{\text{.32 m}}$ 

Now, radius of the inner circle(r`) $ = {\text{ 19  -  10  =  9 m}}$ 

$\therefore $ circumference of inner circle =  2 $\pi r$ $ = {\text{ 2 x 3}}{\text{.14 x 9  =  56}}{\text{.52 m}}$

Hence, the circumference of inner and outer circles are ${\text{56}}{\text{.52 m and 119}}{\text{.32 m respectively}}$ 

16. How many times a wheel of radius $28{\text{ cm}}$ must rotate to go $352{\text{ m}}$? (take  $\pi = \dfrac{{{\text{22}}}}{{\text{7}}}$ )

Ans:

Let the wheel rotate n times of its circumference.

Given, radius of the wheel $ = {\text{ 28 cm}}$ 

And total distance $ = {\text{ 352 m  =  35200 cm}}$ 

$\therefore $ distance covered by wheel $ = {\text{ n x circumference of wheel}}$

$\Rightarrow$ 35200  =  n x $2\pi r $

$\Rightarrow {\text{ 35200  =  n x 2 x }}\dfrac{{22}}{7}{\text{ x 28}} $

$\Rightarrow {\text{ n  =  }}\dfrac{{35200{\text{ x 7}}}}{{2{\text{ x 22 x 28}}}} $

$\Rightarrow {\text{ n  =  200 revolutions}} $ 

Thus wheel must rotate $200$times to go $352{\text{ m}}$ .

17. The minute hand of a circular clock is ${\text{15 cm}}$ long. How far does the tip of the minute hand move in 1 hour? (Take $\pi {\text{  =  3}}{\text{.14}}$)

Ans:

In 1 hour, a minute hand completes one round means makes a circle.

Given, radius of the circle(r) $ = {\text{ 15 cm}}$ 

Circumference of the circular clock =  2 $\pi r$  =  $2 x 3{\text{.14 x 15  =  94}}{\text{.2 cm}}$ 

Hence, the tip of the minute hand moves $94.2{\text{ cm}}$ in $1$ hour.

Conversion of Units

We have:

Note: Since,   1m = 100 cm ∴ 1 m2 = 10000 cm2

1 km = 1000 m ∴ 1 km2 = 10,00,000 m2

1 hectare (ha) = 100 m x 100m = 10000 m2

Overview of Deleted Syllabus for CBSE Class 7 Maths Perimeter and Area

Class 7 Maths Chapter 9: Exercises Breakdown

Conclusion

NCERT Solutions for Maths Perimeter and Area Chapter 9 Class 7 Maths by Vedantu equips you with essential tools to measure and compare shapes. This chapter focuses on calculating the distance around a closed figure (perimeter) and the amount of space enclosed by that figure (area). This chapter is crucial for building a strong foundation in geometry. By understanding the concepts of perimeter and area, students can solve various practical problems and prepare themselves for more advanced topics in mathematics. In previous year exams, around 3-4, questions have been asked from this chapter, highlighting its significance in the overall curriculum. By thoroughly practising the problems and understanding the step-by-step solutions provided by Vedantu, you can confidently tackle algebraic expressions and identities.

Other Study Material for CBSE Class 7 Maths Chapter 9

Chapter-Specific NCERT Solutions for Class 7 Maths

Given below are the chapter-wise NCERT Solutions for Class 7 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

Important Related Links for NCERT Class 7 Maths

Access these essential links for NCERT Class 7 Maths, offering comprehensive solutions, study guides, and additional resources to help students master language concepts and excel in their exams.