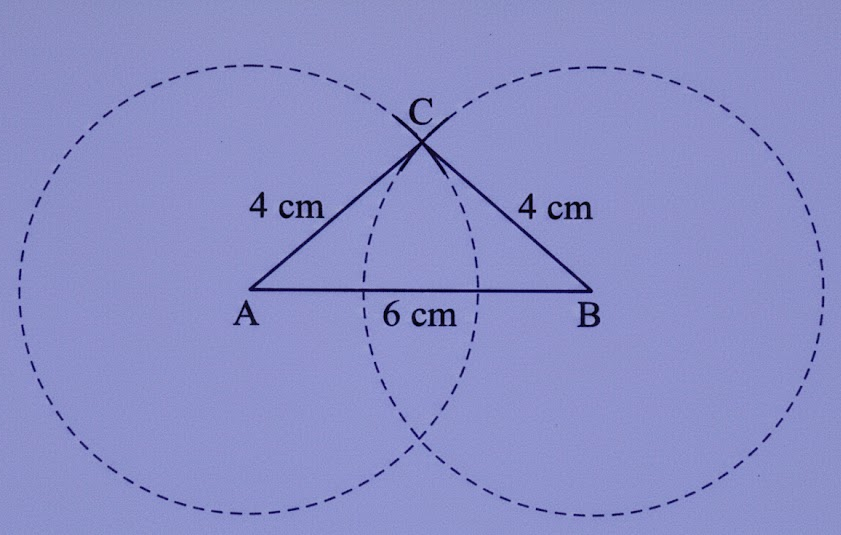
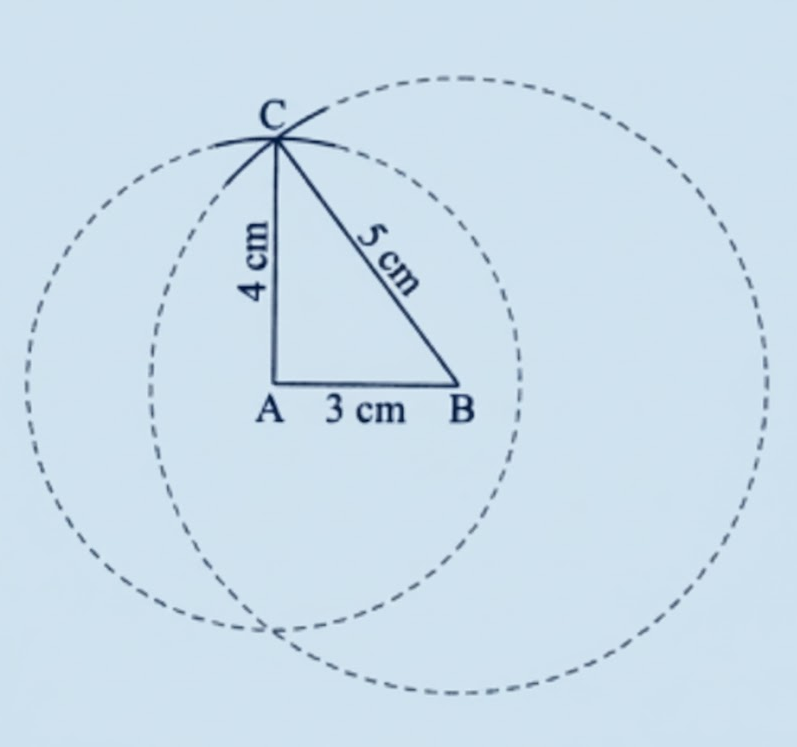
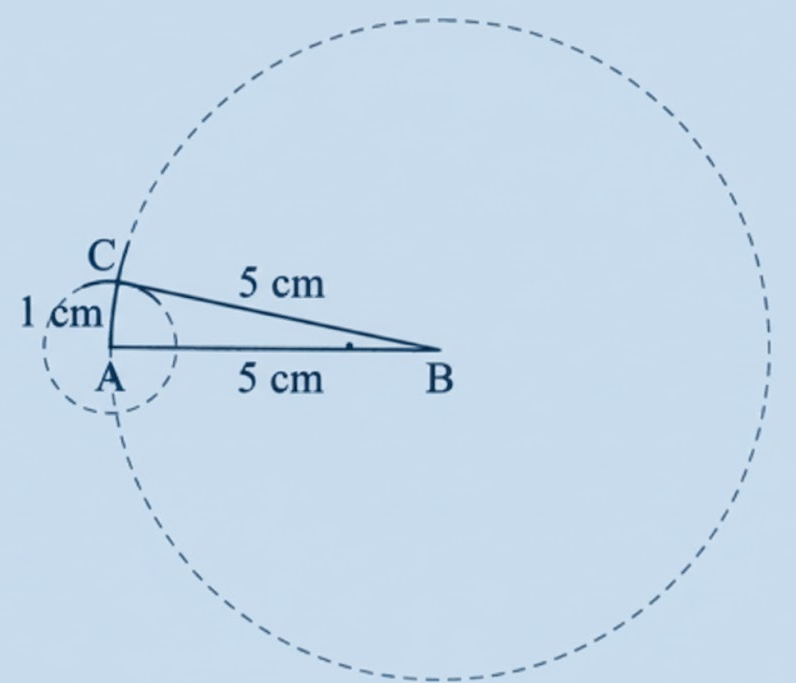
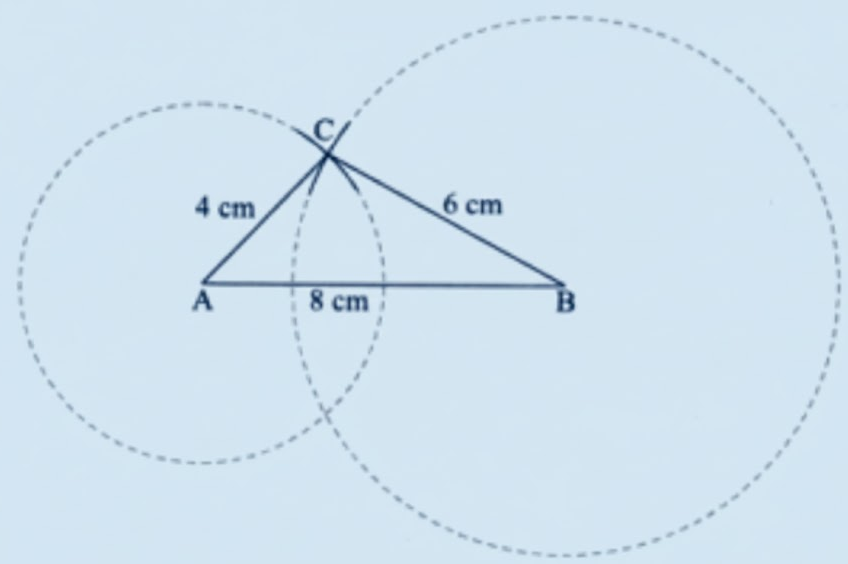
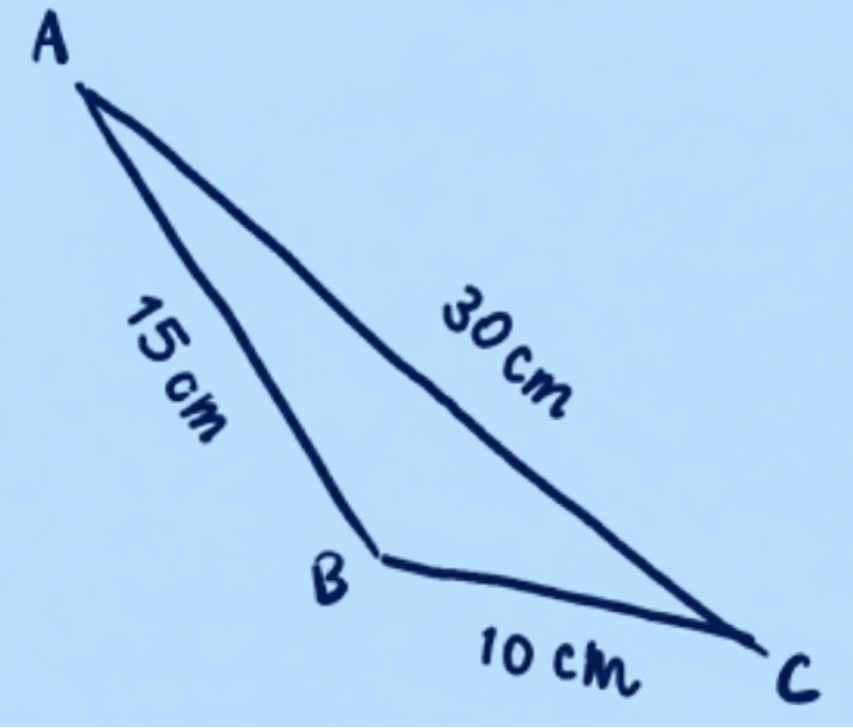
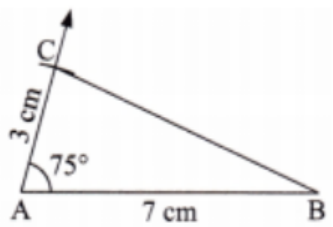
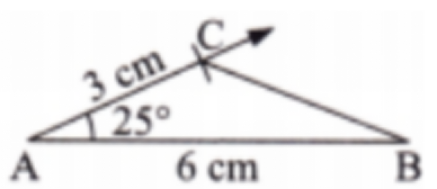
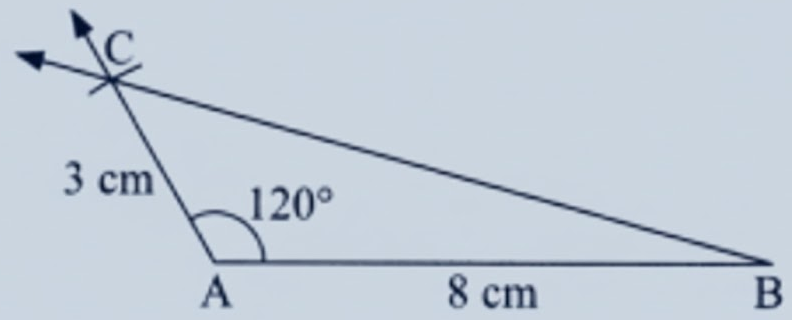
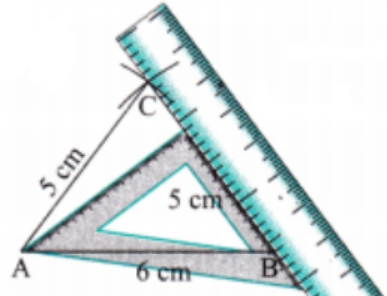
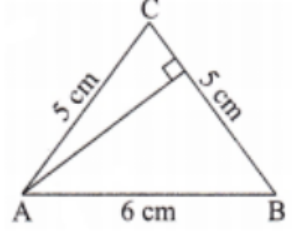
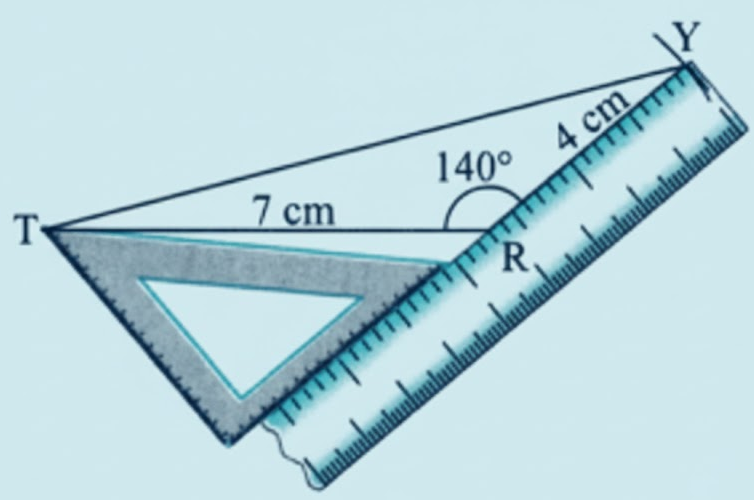
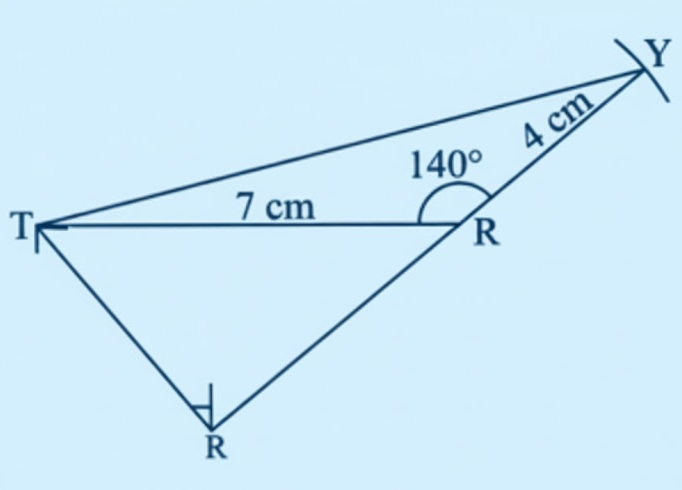
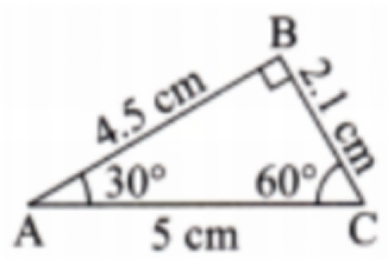
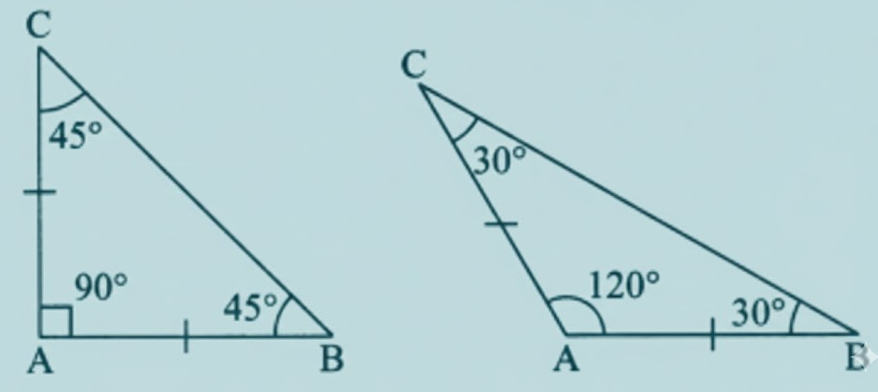
Exercise-wise Solutions for Class 7 Maths Chapter 7 (With Diagrams & Tips)
FAQs on NCERT Solutions For Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines (2025-26)
1. What is covered in NCERT Solutions for Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines?
NCERT Solutions for Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines covers stepwise solutions for all textbook exercises, intext questions, back exercises, and important diagrams.
- Includes definitions, solved examples, and key formulae
- Follows the CBSE 2025–26 syllabus for maximum exam alignment
- Provides exam-oriented answers for better marks
- Offers free PDF downloads and revision strategies
2. How to write stepwise NCERT answers to score full marks in Class 7 Maths Chapter 7?
To score full marks with NCERT Solutions for Class 7 Maths Chapter 7, ensure
- Each step is shown clearly as per the marking scheme
- Proper use of definitions and diagrams where required
- Numbering each step within calculations or logical reasoning
- Highlighting key terms and final answers
- Following the CBSE answer structuring guidelines strictly
3. Are diagrams or definitions necessary in Class 7 Maths Chapter 7 answers?
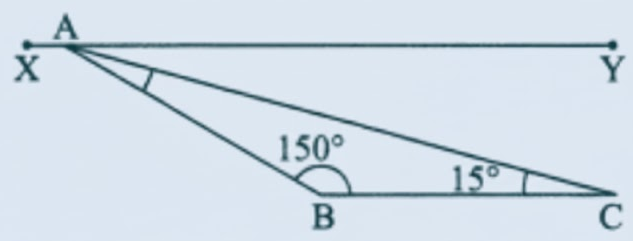
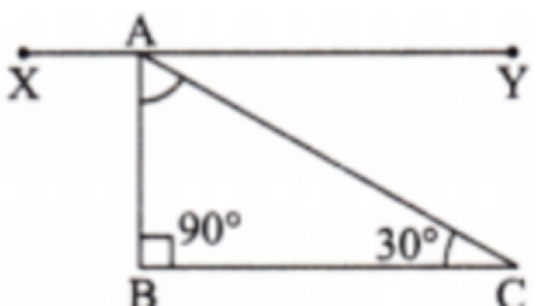
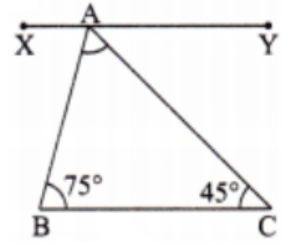
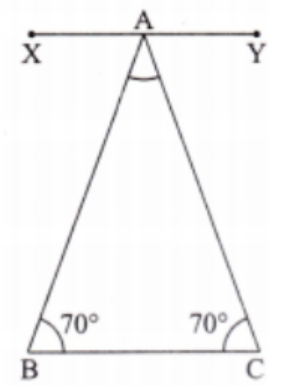
Yes, adding diagrams and clear definitions is often necessary in NCERT Solutions for Class 7 Maths Chapter 7:
- Diagrams: Help score easy marks and make explanations clear
- Definitions: Show conceptual understanding
- Always label diagrams neatly and use correct mathematical terms as per syllabus
4. Where can I download free PDF of Class 7 Maths Chapter 7 NCERT Solutions?
You can download the free PDF of NCERT Solutions for Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines from trusted educational websites.
- Look for the official PDF download button on solution pages
- Ensure alignment with CBSE 2025–26 syllabus
- Use the PDF for offline revision and practice
5. Which questions from Chapter 7 are likely to appear in CBSE school exams?
Important questions from NCERT Chapter 7 often appear in CBSE exams, especially:
- Back exercise and intext NCERT questions
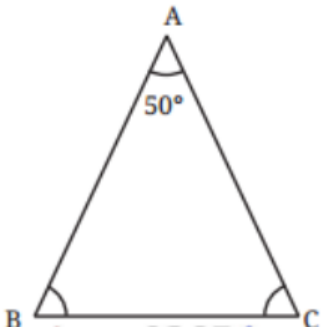
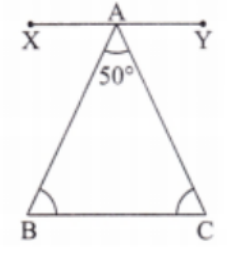
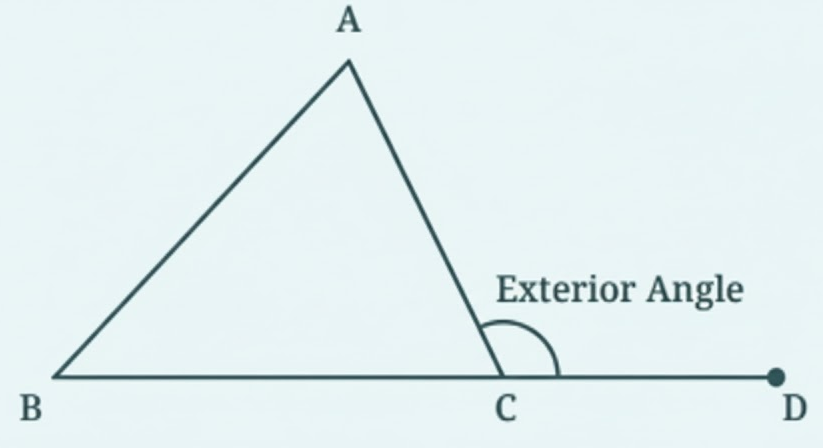
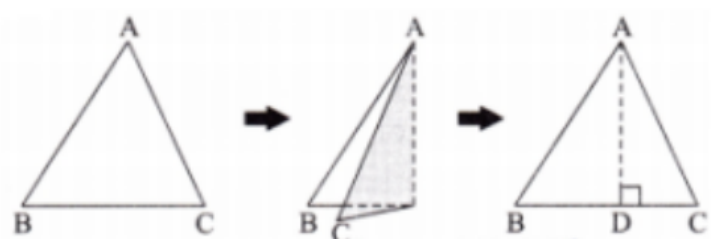
- Definitions and properties of angles formed by intersecting lines
- Diagram-based reasoning questions
- Application-based problems as seen in exam patterns
6. How do I structure long answers in Class 7 Maths Chapter 7 for maximum marks?
To structure long answers for NCERT Solutions Class 7 Maths Chapter 7 and score better:
- Begin with a brief definition or formula
- Draw a neatly labelled diagram if required
- Break the solution into numbered steps
- Highlight key results and final answer
7. How does using stepwise, exam-oriented solutions for Class 7 Maths Chapter 7 improve accuracy and confidence?
Stepwise, exam-oriented NCERT Solutions for Class 7 Maths Chapter 7 build accuracy and confidence by:
- Matching the CBSE marking scheme
- Making error spotting easier
- Reinforcing mathematical reasoning and logic
- Helping practice presentation style for real exams
8. Do examiners award partial marks for correct steps even if the final answer is wrong?
Yes, according to CBSE marking scheme for Class 7 Maths:
- Partial marks are given for correct steps shown
- Even if the final answer is incorrect, presenting clear, logical steps can earn marks
- Always show all the working to maximise your score
9. What are the key definitions and formulae from Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines?
Key definitions and formulae from NCERT Class 7 Maths Chapter 7 include:
- Intersecting lines: Lines that meet at a point
- Vertically opposite angles: Equal angles formed when two lines intersect
- Linear pair: Two adjacent angles whose sum is 180°
- Basic angle formula: Angle properties used in problems
Ensure to learn and write these in your answers for scoring full marks.
10. How can I quickly revise Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines before exams?
For fast revision before exams:
- Review stepwise NCERT Solutions and key definitions
- Go through important diagrams and labelling
- Practice with worksheets and extra questions
- Use revision notes and the NCERT Solutions PDF for last-minute preparation
This targeted approach improves speed and exam confidence.