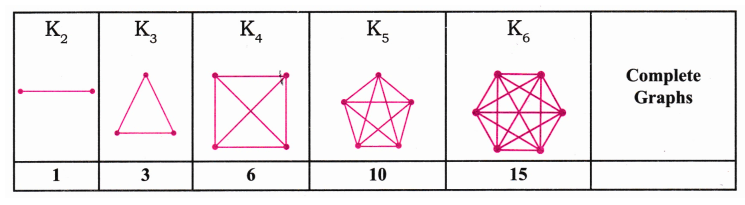
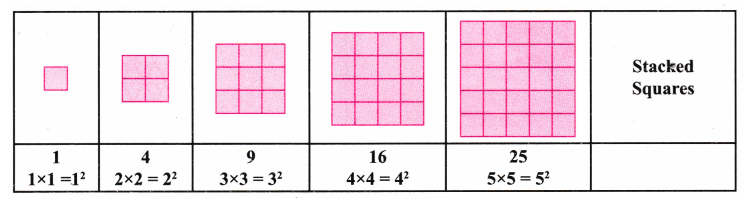
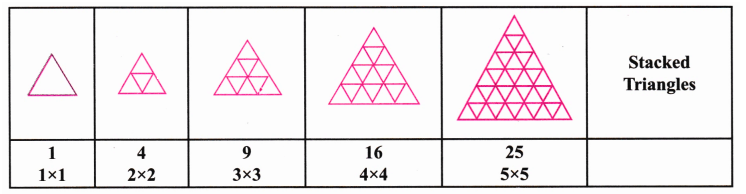
Patterns in Mathematics - Exercise-wise Questions and Answers For Class 6 Maths - Free PDF Download
FAQs on NCERT Solutions For Class 6 Maths Chapter 1 Patterns in Mathematics - 2025-26
1. Where can I find accurate, step-by-step NCERT Solutions for Class 6 Maths Chapter 1 for the 2025-26 session?
You can find the latest CBSE 2025-26 pattern solutions for Class 6 Maths Chapter 1, 'Knowing Our Numbers,' on Vedantu. These solutions are prepared by subject experts and provide detailed, step-by-step explanations for every question in the NCERT textbook, ensuring they are accurate and easy to follow.
2. What is the correct method for solving problems on comparing large numbers as per the NCERT solutions?
The NCERT Solutions explain a simple two-step method. First, count the number of digits in each number; the number with more digits is greater. If the number of digits is the same, you must compare the digits starting from the leftmost place value. The number with the larger digit at the first point of difference is considered the greater number.
3. How do the NCERT Solutions explain placing commas in both Indian and International Systems of Numeration?
The solutions provide clear, step-by-step guidance on this topic:
- In the Indian System, the first comma is placed after the hundreds place (three digits from the right). Subsequent commas are placed after every two digits, correctly separating thousands, lakhs, and crores.
- In the International System, commas are consistently placed after every three digits from the right, which helps separate thousands, millions, and billions.
4. What is the step-by-step process for estimating a sum by rounding off, as shown in the solutions?
The solutions for estimation problems guide you to first round off each number to its greatest place value (or as specified in the question). For instance, to estimate 5,290 + 17,986, you would round 5,290 to 5,000 and 17,986 to 18,000. Finally, you add the rounded-off numbers (e.g., 5,000 + 18,000 = 23,000) to arrive at the estimated sum.
5. How do the NCERT solutions for Chapter 1 break down the rules for writing Roman numerals?
The NCERT Solutions simplify Roman numerals by explaining the core rules methodically:
- Symbols like I, X, and C can be repeated up to three times in a row.
- A smaller value symbol written to the right of a larger value symbol is added (e.g., VI = 5 + 1 = 6).
- A smaller value symbol written to the left of a larger value symbol is subtracted (e.g., IX = 10 - 1 = 9).
- The symbols V, L, and D are never subtracted.
6. Why is it important to learn both the Indian and International systems of numeration? How do the solutions clarify their practical use?
Learning both systems is crucial for understanding numbers in different real-world contexts. The Indian system (Lakhs, Crores) is used within India for finance, population, and media reports. The International system (Millions, Billions) is used globally. The NCERT solutions clarify this by providing examples that show how the same large number is read differently in each system, helping students avoid confusion when interpreting large-scale data from various sources.
7. Beyond getting the right answer, how does following the step-by-step NCERT solutions for estimation improve mathematical thinking?
Following the step-by-step method for estimation builds strong mental maths skills and number sense. It teaches you to quickly check the reasonableness of a calculation. For example, if your exact answer is very different from your estimated answer, it signals that you should re-check your calculation for errors. This is a practical skill for everyday situations like creating a budget or checking a shopping bill.
8. What common mistakes do students make in Roman numerals, and how do these solutions help prevent them?
A very common mistake is subtracting symbols incorrectly, such as writing 'IC' for 99 instead of the correct XCIX. The NCERT solutions prevent such errors by reinforcing the rule that a symbol can only be subtracted from the next one or two greater symbols (e.g., 'I' can be subtracted from 'V' and 'X' only, not 'C'). By providing solved examples for tricky numbers, the solutions build a strong conceptual foundation and prevent these common errors.