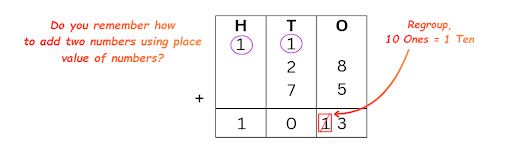
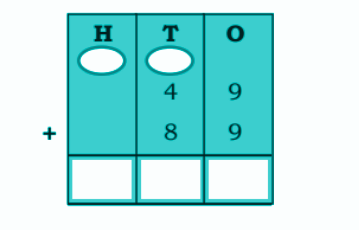
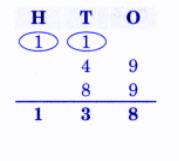
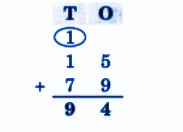
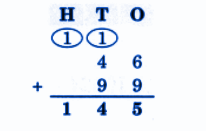
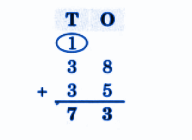
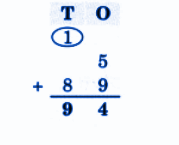
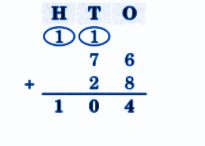
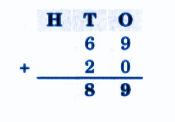
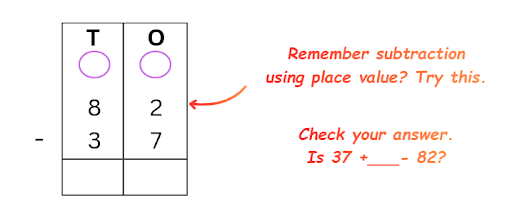
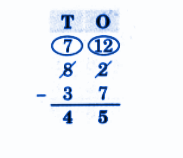
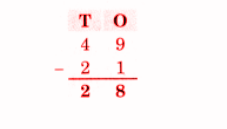
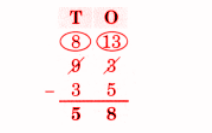
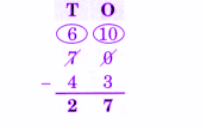
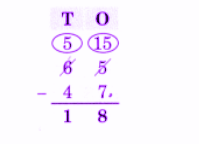
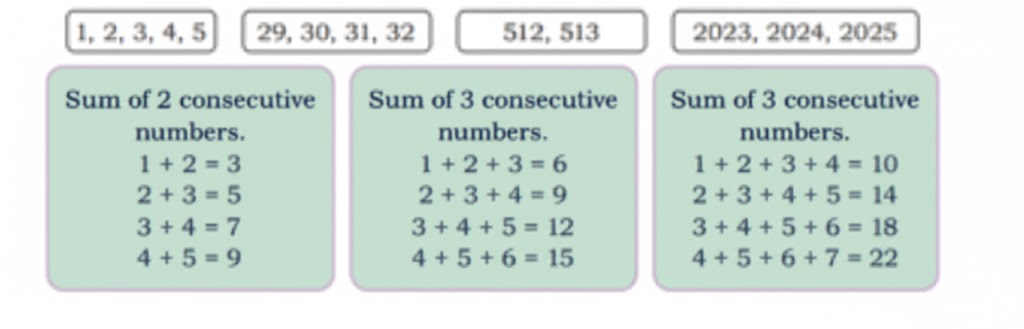
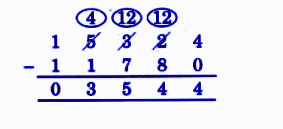
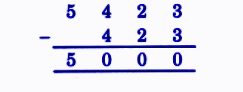
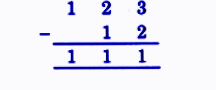
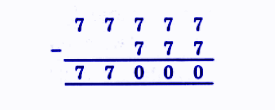
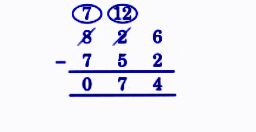
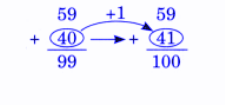
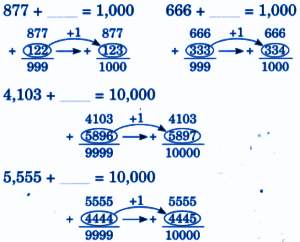
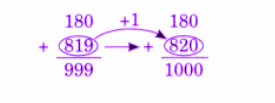
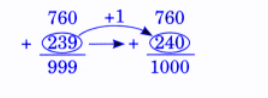
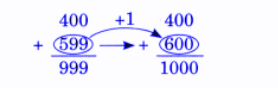
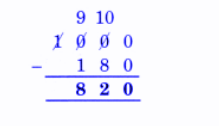
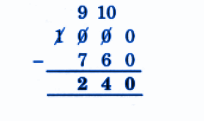
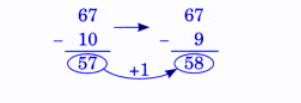
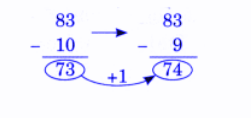
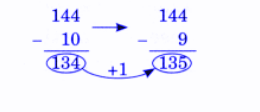
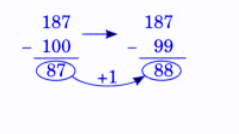
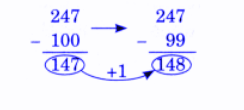
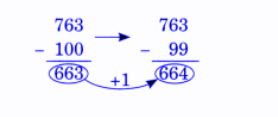
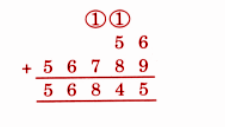
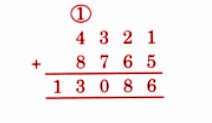
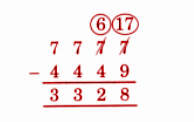
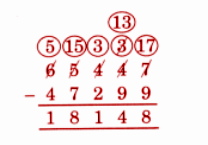
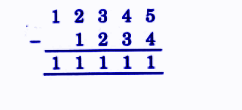
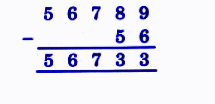
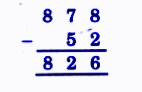
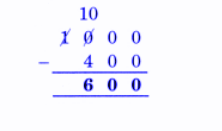Exercise-wise NCERT Answers for The Travellers II Class 5 Maths
FAQs on NCERT Solutions For Class 5 Maths Chapter 4 We The Travellers-Ii - 2025-26
1. What is covered in NCERT Solutions Class 5 Maths Mela Chapter 4 The Travellers—II?
NCERT Solutions Class 5 Maths Mela Chapter 4 The Travellers—II provides stepwise answers to all exercise and intext questions, matching CBSE 2025–26 requirements.
- Complete stepwise solutions for every question
- Clear diagrams and exam-aligned explanations
- Definitions, formulae, and important concepts
- Helpful for scoring full marks in CBSE Class 5 Maths exams
2. How to score full marks in The Travellers II?
To score full marks in Class 5 Maths Chapter 4 The Travellers II, students should follow structured steps:
- Write stepwise answers as shown in NCERT Solutions
- Include clear diagrams and labels where needed
- Use keywords and definitions from the syllabus
- Show all calculation steps for stepwise marking
- Revise important topics and practice with sample questions
3. Is diagram compulsory in class 5 maths chapter 4?
Diagrams are often required in answers for Chapter 4, especially for questions involving measurements or journey maps.
- Use neat, well-labelled diagrams for full marks
- Diagrams help illustrate concepts like distance or directions
- Always check if your answer includes a visual component in the textbook or solutions
- Marking schemes may allocate specific marks for diagrams
4. Where to get pdf of NCERT solutions class 5 maths?
You can download the free PDF of NCERT Solutions for Class 5 Maths Chapter 4 from trusted educational platforms.
- Look for the “Free PDF Download” button on the solutions page
- PDF covers all stepwise answers, diagrams, and revision notes
- Use the PDF for offline study and quick revision before exams
5. What are key concepts in Chapter 4 The Travellers II?
Class 5 Maths Chapter 4 The Travellers II focuses on:
- Distance, Time, and Measurement
- Reading and drawing maps or routes
- Stepwise problem solving using real-life travel scenarios
- Application of basic arithmetic in practical journeys
- Understanding directions and landmarks
6. What is the marking scheme for chapter 4?
The marking scheme for Class 5 Maths Chapter 4 is based on stepwise accuracy, correct diagrams, and key terms.
- 1–2 marks for definitions or direct answers
- 2–4 marks for stepwise solutions
- Separate marks for diagrams/maps if asked
- Additional marks for using correct keywords and calculation steps
- Always break answers into neat, labelled steps for best marks
7. How to present long answers to match CBSE marking?
For long answers in CBSE Class 5 Maths:
- Write in logical steps, each step on a separate line
- Show all calculations and working
- Add diagrams or maps if relevant, and label them neatly
- Use headings or underline important keywords
- Check marking scheme to include all required points
8. How to learn diagrams/maps for this chapter?
To master diagrams and map questions in Chapter 4:
- Practice by drawing maps/diagrams from the textbook and solutions
- Label directions (North, South, East, West) and important points
- Use a ruler for neatness and clarity
- Revise common labels and symbols before exams
9. Are NCERT Solutions enough for Class 5 Maths exams?
NCERT Solutions provide comprehensive coverage for exam preparation.
- They follow the latest CBSE syllabus
- Include stepwise answers and important topics
- Useful for concept clarity and practice
- Supplement with practice questions for extra confidence
10. Where can I get chapterwise solutions PDF for offline study?
Chapterwise solutions PDFs for Class 5 Maths NCERT can be downloaded from reliable educational websites.
- Look for the ‘Download PDF’ option on the solutions page
- Ensure you select the latest academic year (2025–26) PDF
- Use PDFs for offline revision and preparation anytime
11. What are the most important topics from this chapter?
The most important topics from Class 5 Maths Chapter 4 are:
- Calculating distance and time using real-life examples
- Drawing and interpreting travel maps
- Stepwise problem solving involving routes and journeys
- Labelling diagrams and following directions
- Understanding and applying key definitions
12. Do examiners award partial marks for correct steps even if the final answer is wrong?
Yes, CBSE marking scheme gives partial marks for correct steps and method, even if the final answer is incorrect.
- Always write each calculation step clearly
- Show full working and reasoning
- Attempt every part of the question to gain possible marks
- Even with a small mistake, you can score for method and presentation