NCERT Solutions for Class 11 Maths Miscellaneous Exercise Chapter 9 - Straight Lines

Miscellaneous Exercise

1. Find the value of ${\text{k}}$ for which the line $(k - 3)x - \left( {4 - {k^2}} \right)y + {k^2} - 7k + 6 = 0$ is

(a) Parallel to $x$-axis

Ans: The given equation of line is $(k - 3)x - \left( {4 - {k^2}} \right)y + {k^2} - 7k + 6 = 0$

If the line is parallel to $x$-axis,

Slope of the line \[ = \] Slope of the $x$-axis

It can be written as,

$\left( {4 - {k^2}} \right)y = (k - 3)x + {k^2} - 7k + 6 = 0$

We get,

$y = \dfrac{{(k - 3)}}{{\left( {4 - {k^2}} \right)}}x + \dfrac{{{k^2} - 7k + 6}}{{\left( {4 - {k^2}} \right)}}$, Which is of the form $y = mx + c$

Here, the slope of the given line$ = \dfrac{{(k - 3)}}{{\left( {4 - {k^2}} \right)}}$

Consider the slope of $x$-axis $ = 0$

$\dfrac{{(k - 3)}}{{\left( {4 - {k^2}} \right)}} = 0$

$k - 3 = 0$

$k = 3$

Therefore, if the given line is parallel to the $x$-axis, then the value of $k$ is \[3\].

(b) Parallel to $y$-axis

Ans: The given equation of line is $(k - 3)x - \left( {4 - {k^2}} \right)y + {k^2} - 7k + 6 = 0$

Here if the line is parallel to the \[y\]-axis, it is vertical and the slope will be undefined.

So, the slope of the given line$ = \dfrac{{(k - 3)}}{{\left( {4 - {k^2}} \right)}}$

Here, $\dfrac{{(k - 3)}}{{\left( {4 - {k^2}} \right)}}$ is undefined at ${k^2} = 4$

${k^2} = 4$

$ \Rightarrow k =  \pm 2$

Therefore, if the given line is parallel to the $y$-axis, then the value of $k$ is $ \pm 2$.

(c) Passing through the origin.

Ans: The given equation of line is $(k - 3)x - \left( {4 - {k^2}} \right)y + {k^2} - 7k + 6 = 0$

Here, if the line is passing through $(0,0)$ which is the origin satisfies the given equation 

of line,

$(k - 3)(0) - \left( {4 - {k^2}} \right)(0) + {k^2} - 7k + 6 = 0$

${k^2} - 7k + 6 = 0$

Separate the terms,

${k^2} - 6k - k + 6 = 0$

$(k - 6)(k - 1) = 0$

$k = 1\,\,{\text{or }}\,{\text{6}}$ 

Therefore, if the given line is passing through the origin, then the value of $k$ is either 

$1\,\,{\text{or }}\,{\text{6}}$.

2. Find the equation of the line, which cut-off intercepts on the axes whose sum and product are \[1\]and $ - 6$, respectively.

Ans: Consider, the intercepts cut by the given lines on the axes are \[a\]and \[b.\]

$a + b = 1 \to (1)$ (1)

$ab =  - 6 \to (2)$

Solve both equations to get

$a = 3$ and $b =  - 2$ or $a =  - 2$ and $b = 3$

We know that the equation of the line whose intercepts on a and $b$ axes is

$\dfrac{x}{a} + \dfrac{y}{b} = 1$ or $bx + ay - ab = 0$

Case 1: $a = 3$ and $b =  - 2$

Now, the equation of the line is $ - 2x + 3y + 6 = 0$

That is, $2x - 3y = 6$

Case 2: $a =  - 2$ and $b = 3$

Now, the equation of the line is $3x - 2y + 6 = 0$

That is,$ - 3x + 2y = 6$

Therefore, the required equation of the lines are $2x - 3y = 6$ and $ - 3{\text{x}} + 2{\text{y}} = 6$.

3. What are the points on the $y$-axis whose distance from line $\dfrac{x}{3} + \dfrac{y}{4} = 1$ is \[4\] units.

Ans: Consider $(0,b)$ as the point on the $y$-axis whose distance from line $\dfrac{x}{3} + \dfrac{y}{4} = 1$ is  4 units.

It can be written as \[4x + 3y - 12 = 0 \to (1)\]

Compare equation \[\left( 1 \right)\] to the general equation of line $Ax + Bx + C = 0$, we get

$A = 4,\;\,B = 3$ and $C =  - 12$

We know that the perpendicular distance \[\left( d \right)\] of a line $Ax + By + C = 0$ from $\left( {{x_1},{y_1}} \right)$ is,

$d = \dfrac{{\left| {A{x_1} + B{y_1} + C} \right|}}{{\sqrt {{A^2} + {B^2}} }}$

If $(0,b)$ is the point on the $y$-axis whose distance from line $\dfrac{x}{3} + \dfrac{y}{4} = 1$  is \[4\] units, then

$4 = \dfrac{{|4(0) + 3(b) - 12|}}{{\sqrt {{4^2} + {3^2}} }}$

$4 = \dfrac{{|3b - 12|}}{5}$

By cross multiplication,

$20 = |3b - 12|$

$20 =  \pm (3b - 12)$

Here, $20 = (3b - 12)$ or $20 =  - (3b - 12)$

It can be written as

$3b = 20 + 12$ or $3b =  - 20 + 12$

Now we get,

$b = \dfrac{{32}}{3}$ or $b = \dfrac{{ - 8}}{3}$

Therefore, the required points are $b = \dfrac{{32}}{3}$ and $b = \dfrac{{ - 8}}{3}$.

4. Find the perpendicular distance from the origin to the line joining the points $(\cos \theta,\sin \theta )\operatorname{and} (\cos \phi,\sin \phi )$

Ans: The equation of the line joining the points $(\cos \theta ,\sin \theta )$ and $(\cos \phi ,\sin \phi )$ is,

$(\cos \theta ,\sin \theta )\operatorname{and} (\cos \phi ,\sin \phi )$

$y - \sin \theta  = \dfrac{{\sin \phi  - \sin \theta }}{{\cos \phi  - \cos \theta }}(x - \cos \theta )$

By cross multiplication,

$y(\cos \phi  - \cos \theta ) - \sin \theta (\cos \phi  - \cos \theta ) = x(\sin \phi  - \sin \theta ) - \cos \theta (\sin \phi  - \sin \theta )$

$x(\sin \theta  - \sin \phi ) + y(\cos \phi  - \cos \theta ) + \cos \theta \sin \phi  - \cos \theta \sin \theta  - \sin \theta \cos \phi  + \sin \theta \cos \theta  = 0$

$x(\sin \theta  - \sin \phi ) + y(\cos \phi  - \cos \theta ) + \sin (\phi  - \theta ) = 0$

$Ax + By + C = 0$, where $A = \sin \theta  - \sin \phi ,B = \cos \phi  - \cos \theta $, and $C = \sin (\phi  - \theta )$

It is known that the perpendicular distance \[\left( d \right)\]of a line $Ax + By + C = 0$ from a point 

$\left( {{x_1},{y_1}} \right)$ is,

$d = \dfrac{{\left| {A{x_1} + B{y_1} + C} \right|}}{{\sqrt {{A^2} + {B^2}} }}$

Thus, the perpendicular distance \[\left( d \right)\] of the given line from point $\left( {{x_1},{y_1}} \right) = (0,0)$ is,

$d = \dfrac{{|(\sin \theta  - \sin \phi )(0) + (\cos \phi  - \cos \theta )(0) + \sin (\phi  - \theta )|}}{{\sqrt {{{(\sin \theta  - \sin \phi )}^2} + {{(\cos \phi  - \cos \theta )}^2}} }}$

$ = \dfrac{{|\sin (\phi  - \theta )|}}{{\sqrt {{{\sin }^2}\theta  + {{\sin }^2}\phi  - 2\sin \theta \sin \phi  + {{\cos }^2}\phi  + {{\cos }^2}\theta  - 2\cos \phi \cos \theta } }}$

Group the terms,

$ = \dfrac{{|\sin (\phi  - \theta )|}}{{\sqrt {\left( {{{\sin }^2}\theta  + {{\cos }^2}\theta } \right) + \left( {{{\sin }^2}\phi  + {{\cos }^2}\phi } \right) - 2(\sin \theta \sin \phi  + \cos \phi \cos \theta )} }}$

$ = \dfrac{{|\sin (\phi  - \theta )|}}{{\sqrt {1 + 1 - 2(\cos (\phi  - \theta ))} }}$

$ = \dfrac{{|\sin (\phi  - \theta )|}}{{\sqrt {2(1 - \cos (\phi  - \theta ))} }}$

$ = \dfrac{{|\sin (\phi  - \theta )|}}{{\sqrt {2\left( {2{{\sin }^2}\left( {\dfrac{{\phi  - \theta }}{2}} \right)} \right)} }}$

$ = \dfrac{{|\sin (\phi  - \theta )|}}{{2\sin \left( {\dfrac{{\phi  - \theta }}{2}} \right)}}$

Therefore, the perpendicular distance from the origin to the line joining the points 

$(\cos \theta ,\sin \theta )\operatorname{and} (\cos \phi ,\sin \phi )$is $\dfrac{{|\sin (\phi  - \theta )|}}{{2\sin \left( {\dfrac{{\phi  - \theta }}{2}} \right)}}$.

5. Find the equation of the line parallel to $y$-axis and draw through the point of intersection of the lines $x - 7y + 5 = 0$ and $3x + y = 0$.

Ans: The equation of any line parallel to the \[y\]-axis is of the form $x = a \to (1)$

The two given lines are $x - 7y + 5 = 0 \to (2)$

$3x + y = 0 \to (3)$

Solve equation \[\left( 2 \right)\] and \[\left( 3 \right)\], we get $x =  - \dfrac{5}{{22}}$ and $y = \dfrac{{15}}{{22}}$ 

Thus, $\left( { - \dfrac{5}{{22}},\dfrac{{15}}{{22}}} \right)$ is the point of intersection of lines $(2)$ and \[\left( 3 \right).\]

Since line $x = a$ passes through point $\left( { - \dfrac{5}{{22}},\dfrac{{15}}{{22}}} \right),\,\,$

$a =  - \dfrac{5}{{22}}$

Therefore, the required equation of the line is $x =  - \dfrac{5}{{22}}$.

6. Find the equation of a line drawn perpendicular to the line $\dfrac{x}{4} + \dfrac{y}{6} = 1$ through the point, where it meets the $y$-axis.

Ans: Here, the equation of the given line is $\dfrac{x}{4} + \dfrac{y}{6} = 1$ 

This equation can be written as $3x + 2y - 12 = 0$ 

Rewrite as,

$y = \dfrac{{ - 3}}{2}x + 6$, which is of the form $y = mx + c$

Now, Slope of the given line $ = \dfrac{{ - 3}}{2}$

$\therefore $ Slope of line perpendicular to the given line $ =  - \dfrac{1}{{\left( { - \dfrac{3}{2}} \right)}} = \dfrac{2}{3}$ 

Let the given line intersect the \[y\]-axis at $(0,y)$. 

Substitute $x$ with 0 in the equation of the given line, 

$\dfrac{y}{6} = 1 \Rightarrow y = 6$ 

$\therefore $ The given line intersects the \[y\]-axis at $(0,6)$. 

The equation of the line that has a slope of $\dfrac{2}{3}$ and passes through point $(0,6)$ is,$(y - 6) = \dfrac{2}{3}(x - 0)$

Cross-multiply and expand brackets,

$3y - 18 = 2x$

$2x - 3y + 18 = 0$

Therefore, the required equation of the line is $2x - 3y + 18 = 0$.

7. Find the area of the triangle formed by the line $y - x = 0,\,\,x + y = 0$ and $x - k = 0$.

Ans: It is given that,

$y - x = 0 \to (1)$ 

$x + y = 0 \to (2)$

$x - k = 0 \to (3)$

Here, the point of intersection of lines \[\left( 1 \right)\]and \[\left( 2 \right)\] is,

$x = 0$ and $y = 0$

The point of intersection of lines $(2)$ and \[\left( 3 \right)\] is,

$x = k$ and $y =  - k$

The point of intersection of lines \[\left( 3 \right)\]and \[\left( 1 \right)\] is,

$x = k$ and $y = k$

Now, the vertices of the triangle formed by the three given lines are $(0,0),\,\,(k, - k)$ and 

$(k,k)$.

Here the area of triangle whose vertices are $\left( {{x_1},{y_1}} \right),\,\,\left( {{x_2},{y_2}} \right)$ and $\left( {{x_3},{y_3}} \right)$ is,

$\dfrac{1}{2}\left| {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right|$

So the area of the triangle formed by the three given lines,

$ = \dfrac{1}{2}|0( - k - k) + k(k - 0) + k(0 + k)|$ square units

$ = \dfrac{1}{2}\left| {{k^2} + {k^2}} \right|$square units

We get,

$ = \dfrac{1}{2}\left| {2{k^2}} \right|$

$ = {k^2}$ square units

Therefore, the area of the triangle formed by the line $y - x = 0,\,\,x + y = 0$ and $x - k = 0$ is 

${k^2}$ square units.

8.Find the value of $p$ so that the three lines $3x + y - 2 = 0,\,\,px + 2y - 3 = 0$ and $2x - y - 3 = 0$ may intersect at one point.

Ans: It is given that,

$3x + y - 2 = 0 \to (1)$

$px + 2y - 3 = 0 \to (2)$

$2x - y - 3 = 0 \to (3)$

Solve equations \[\left( 1 \right)\] and \[\left( 3 \right)\] to get

$x = 1$ and $y =  - 1$

Here, the three lines intersect at one point and the point of intersection of lines \[\left( 1 \right)\] and

\[\left( 3 \right)\]will also satisfy line \[\left( 2 \right)\]

$p(1) + 2( - 1) - 3 = 0$

$ \Rightarrow p - 2 - 3 = 0$

$ \Rightarrow p = 5$

Therefore, the value of $p$ is \[5\].

9. If three lines whose equations are $y = {m_1}x + {c_1},\,\,y = {m_2}x + {c_2}$, and $y = {m_2}x + {c_2}$ are concurrent, then show that ${m_1}\left( {{c_2} - {c_3}} \right) + {m_2}\left( {{c_3} - {c_1}} \right) + {m_3}\left( {{c_1} - {c_2}} \right) = 0$.

Ans: It is given that,

$y = {m_1}x + {c_1} \to (1)$

$y = {m_2}x + {c_2} \to (2)$

$y = {m_3}x + {c_3} \to (3)$

Subtract equation \[\left( 1 \right)\]from \[\left( 2 \right)\],

$0 = \left( {{m_2} - {m_1}} \right)x + \left( {{c_2} - {c_1}} \right)$

$ \Rightarrow \left( {{m_1} - {m_2}} \right)x = {c_2} - {c_1}$

$x = \dfrac{{{c_2} - {c_1}}}{{{m_1} - {m_2}}}$

Substitute this value in equation \[\left( 1 \right)\] 

$y = {m_1}\left( {\dfrac{{{c_2} - {c_1}}}{{{m_1} - {m_2}}}} \right) + {c_1}$

Multiply the terms,

$y = \dfrac{{{m_1}{c_2} - {m_1}{c_1}}}{{{m_1} - {m_2}}} + {c_1}$

Take LCM,

$y = \dfrac{{{m_1}{c_2} - {m_1}{c_1} + {m_1}{c_1} - {m_2}{c_1}}}{{{m_1} - {m_2}}}$

$ \Rightarrow y = \dfrac{{{m_1}{c_2} - {m_2}{c_1}}}{{{m_1} - {m_2}}}$

Here,

$\left( {\dfrac{{{c_2} - {c_1}}}{{{m_1} - {m_2}}},\dfrac{{{m_1}{c_2} - {m_2}{c_1}}}{{{m_1} - {m_2}}}} \right)$ is the point of intersection of lines $(1)$ and \[\left( 2 \right)\]

Lines \[\left( 1 \right),{\text{ }}\left( 2 \right)\]and \[\left( 3 \right)\] are concurrent. So the point of intersection of lines \[\left( 1 \right)\] and \[\left( 2 \right)\]

 will satisfy equation \[\left( 3 \right)\].

$\dfrac{{{m_1}{c_2} - {m_2}{c_1}}}{{{m_1} - {m_2}}} = {m_3}\left( {\dfrac{{{c_2} - {c_1}}}{{{m_1} - {m_2}}}} \right) + {c_3}$

Multiply the terms and take LCM,

$\dfrac{{{m_1}{c_2} - {m_2}{c_1}}}{{{m_1} - {m_2}}} = \dfrac{{{m_3}{c_2} - {m_3}{c_1} + {c_3}{m_1} - {c_3}{m_2}}}{{{m_1} - {m_2}}}$

By cross multiplication,

${m_1}{c_2} - {m_2}{c_1} - {m_3}{c_2} + {m_3}{c_1} - {c_3}\;{m_1} + {c_3}\;{m_2} = 0$

Take out the common terms,

${m_1}\left( {{c_2} - {c_3}} \right) + {m_2}\left( {{c_3} - {c_1}} \right) + {m_3}\left( {{c_1} - {c_2}} \right) = 0$

Therefore, If three lines whose equations are $y = {m_1}x + {c_1},\,\,y = {m_2}x + {c_2}$, and $y = {m_2}x + {c_2}$ 

are concurrent, then ${m_1}\left( {{c_2} - {c_3}} \right) + {m_2}\left( {{c_3} - {c_1}} \right) + {m_3}\left( {{c_1} - {c_2}} \right) = 0$.

10. Find the equation of the line through the points $(3,2)$ which makes an angle of ${45^\circ }$ with the line $x - 2y = 3$

Ans: Let the slope of the required line be ${m_1}$. 

The given line can be written as,

 $y = \dfrac{1}{2}x - \dfrac{3}{2}$, which is of the form $y = mx + c$

Now, slope of the given line is 

${m_2} = \dfrac{1}{2}$ 

It is given that the angle between the required line and line $x - 2y = 3$ is ${45^\circ }$. 

If $\theta $ is the acute angle between lines ${l_1}$ and ${l_2}$ with slopes ${m_1}$ and ${m_2}$ respectively, then

$\tan \theta  = \left| {\dfrac{{{m_2} - {m_1}}}{{1 + {m_1}{m_2}}}} \right|$

${\text{Now, }}\tan {45^\circ } = \dfrac{{\left| {{m_2} - {m_1}} \right|}}{{1 + {m_1}{m_2}}}$

Substitute the values,

$ \Rightarrow 1 = \left| {\dfrac{{\dfrac{1}{2} - {m_1}}}{{1 + \dfrac{{{m_1}}}{2}}}} \right|$

Take LCM,

$ \Rightarrow 1 = \left| {\dfrac{{\left( {\dfrac{{1 - 2{m_1}}}{2}} \right)}}{{\dfrac{{2 + {m_1}}}{2}}}} \right|$

$ \Rightarrow 1 = \left| {\dfrac{{1 - 2{m_1}}}{{2 + {m_1}}}} \right|$

$ \Rightarrow 1 =  \pm \left( {\dfrac{{1 - 2{m_1}}}{{2 + {m_1}}}} \right)$

$ \Rightarrow 1 = \dfrac{{1 - 2{m_1}}}{{2 + {m_1}}}$ or $1 =  - \left( {\dfrac{{1 - 2{m_1}}}{{2 + {m_1}}}} \right)$

$ \Rightarrow 2 + {m_1} = 1 - 2{m_1}$ or $2 + {m_1} =  - 1 + 2{m_1}$

$ \Rightarrow {m_1} =  - \dfrac{1}{3}$ or ${m_1} = 3$

Case 1: ${m_1} = 3$ 

The equation of the line passing through $(3,2)$ and having a slope of \[3\] is,

$y - 2 = 3(x - 3)$

Expand bracket,

$y - 2 = 3x - 9$

$3x - y = 7$

Case 2: ${m_1} =  - \dfrac{1}{3}$

The equation of the line passing through $(3,2)$ and having a slope of $ - \dfrac{1}{3}$ is

$y - 2 =  - \dfrac{1}{3}(x - 3)$

Cross multiply and expand bracket,

$3y - 6 =  - x + 3$

$x + 3y = 9$

Therefore, the equations of the line are $3x - y = 7$ and $x + 3y = 9$.

11. Find the equation of the line passing through the point of intersection of the line $4x + 7y - 3$ $ = 0$ and $2x - 3y + 1 = 0$ that has equal intercepts on the axes.

Ans: Let the equation of the line having equal intercepts on the axes be $\dfrac{x}{a} + \dfrac{y}{a} = 1$

It can be written as,

$x + y = a \to {\text{(1)}}$

Solve equations $4x + 7y - 3 = 0$ and $2x - 3y + 1 = 0$, we get $x = \dfrac{1}{{13}}$ and $y = \dfrac{5}{{13}}$

$\therefore \left( {\dfrac{1}{{13}},\dfrac{5}{{13}}} \right)$ is the point of the intersection of the two given lines. 

Since equation \[\left( 1 \right)\] passes through point $\left( {\dfrac{1}{{13}},\dfrac{5}{{13}}} \right)$, $\dfrac{1}{{13}} + \dfrac{5}{{13}} = a$

$ \Rightarrow a = \dfrac{6}{{13}}$

Thus, Equation \[\left( 1 \right)\] becomes $x + y = \dfrac{6}{{13}}$ that is, $13x + 13y = 6$

Therefore, the required equation of the line $13x + 13y = 16$.

12. Show that the equation of the line passing through the origin and making an angle $\theta $ with the line $y = mx + c$ is $\dfrac{y}{x} = \dfrac{{m \pm \tan \theta }}{{1 \mp m\tan \theta }}$

Ans: Let the equation of the line passing through the origin be ${\text{y}} = {m_1}x$. 

If this line makes an angle of $\theta $ with line $y = mx + c$, then angle $\theta $ is,

$\tan \theta  = \left| {\dfrac{{{m_1} - m}}{{1 + {m_1}m}}} \right|$

Substitute the values,

$ \Rightarrow \tan \theta  = \left| {\dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x}m}}} \right|$

$ \Rightarrow \tan \theta  =  \pm \left( {\dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x}m}}} \right)$

$ \Rightarrow \tan \theta  = \dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x}m}}$ or $\tan \theta  =  - \left( {\dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x}m}}} \right)$

Case 1: $\tan \theta  = \dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x}m}}$

$ \Rightarrow \tan \theta  + \dfrac{y}{x}m\tan \theta  = \dfrac{y}{x} - m$

$ \Rightarrow m + \tan \theta  = \dfrac{y}{x}(1 - m\tan \theta )$

$ \Rightarrow \dfrac{y}{x} = \dfrac{{m + \tan \theta }}{{1 - m\tan \theta }}$

Case 2: $\tan \theta  =  - \left( {\dfrac{{\dfrac{x}{y} - m}}{{1 + \dfrac{y}{x}m}}} \right)$

$\tan \theta  =  - \left( {\dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x}m}}} \right)$

$ \Rightarrow \tan \theta  + \dfrac{y}{x}m\tan \theta  =  - \dfrac{y}{x} + m$

$ \Rightarrow \dfrac{y}{x}(1 + m\tan \theta ) = m - \tan \theta $

Rewrite as,

$ \Rightarrow \dfrac{y}{x} = \dfrac{{m - \tan \theta }}{{1 + m\tan \theta }}$

Hence, it is shown that the equation of the line passing through the origin and making an angle $\theta $with the line $y = mx + c$, is $\dfrac{y}{x} = \dfrac{{m \pm \tan \theta }}{{1 \mp m\tan \theta }}$.

13. In what ratio, the line joining $( - 1,1)$ and $(5,7)$ is divisible by the line $x + y = 4$ ?

Ans: The equation of the line joining the points $( - 1,1)$ and $(5,7)$ is,

$y - 1 = \dfrac{{7 - 1}}{{5 + 1}}(x + 1)$

$y - 1 = \dfrac{6}{6}(x + 1)$

$x - y + 2 = 0 \to (1)$

The equation of the given line is $x + y - 4 = 0 \to (2)$.

The points of intersection of line \[\left( 1 \right)\] and \[\left( 2 \right)\] is $x = 1$ and $y = 3$.

Let point $(1,3)$ divide the line segment joining $( - 1,1)$ and $(5,7)$ in the ratio $1:k$.

Then, by section formula, 

$(1,3) = \left( {\dfrac{{k( - 1) + 1(5)}}{{1 + k}},\dfrac{{k(1) + 1(7)}}{{1 + k}}} \right)$

Simplify,

$ \Rightarrow (1,3) = \left( {\dfrac{{ - k + 5}}{{1 + k}},\dfrac{{k + 7}}{{1 + k}}} \right)$

$ \Rightarrow \dfrac{{ - k + 5}}{{1 + k}} = 1,\,\,\dfrac{{k + 7}}{{1 + k}} = 3$

$\therefore \dfrac{{ - k + 5}}{{1 + k}} = 1$

By cross multiplication,

$ \Rightarrow  - k + 5 = 1 + k$

$ \Rightarrow 2k = 4$

$k=2$
Therefore, the line joining the points $( - 1,1)$ and $(5,7)$ is divided by line $x + y = 4$ in the ratio \[1:2\].

14. Find the distance of the line $4x + 7y + 5 = 0$ from the point $(1,2)$ along the line $2x - y = 0$

Ans: The given lines are $2x - y = 0 \to (1)$

$4x + 7y + 5 = 0 \to (2)$

${\text{P}}(1,2)$ is a point on line\[\left( 1 \right)\]. 

Let ${\text{Q}}$ be the point intersection of line \[\left( 1 \right)\] and \[\left( 2 \right).\]

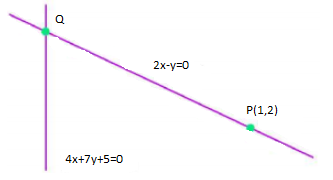
Solve equations \[\left( 1 \right)\] and \[\left( 2 \right)\] to get $x = \dfrac{{ - 5}}{{18}}$ and $y = \dfrac{{ - 5}}{9}$

Now, Coordinates of point $B$ are $\left( {\dfrac{{ - 5}}{{18}},\dfrac{{ - 5}}{9}} \right)$. 

Use distance formula to obtain the distance between points ${\text{P and Q}}$,

${\text{PQ}} = \sqrt {{{\left( {1 + \dfrac{5}{{18}}} \right)}^2} + {{\left( {2 + \dfrac{5}{9}} \right)}^2}} $ units

Take LCM,

$ = \sqrt {{{\left( {\dfrac{{23}}{{18}}} \right)}^2} + {{\left( {\dfrac{{23}}{9}} \right)}^2}} $ units

Rewrite as,

$ = \sqrt {{{\left( {\dfrac{{23}}{{2 \times 9}}} \right)}^2} + {{\left( {\dfrac{{23}}{9}} \right)}^2}} $ units

$ = \sqrt {{{\left( {\dfrac{{23}}{9}} \right)}^2}{{\left( {\dfrac{1}{2}} \right)}^2} + {{\left( {\dfrac{{23}}{9}} \right)}^2}} $ units

$ = \sqrt {{{\left( {\dfrac{{23}}{9}} \right)}^2} + \left( {\dfrac{1}{4} + 1} \right)} $ units

$ = \dfrac{{23}}{9}\sqrt {\dfrac{5}{4}} $ units

$ = \dfrac{{23}}{9} \times \dfrac{{\sqrt 5 }}{2}$ units

$ = \dfrac{{23\sqrt 5 }}{{18}}$ units

Therefore, the required distance is $\dfrac{{23\sqrt 5 }}{{18}}$ units.

15. Find the direction in which a straight line must be drawn through the points $( - 1,2)$ so that its point of intersection with line $x + y = 4$ may be at a distance of \[3\] units from this point.

Ans: Consider $y = mx + c$ as the line passing through the point $( - 1,2)$.

Then, 

$2 = m( - 1) + c$

$ \Rightarrow 2 =  - m + c$

$ \Rightarrow c = m + 2$

Substitute the value of $c$,

$y = mx + m + 2 \to (1)$ 

Now, the given line is,

$x + y = 4 \to (2)$

Solve both equations,

$x = \dfrac{{2 - m}}{{m + 1}}$ and $y = \dfrac{{5m + 2}}{{m + 1}}$

$\left( {\dfrac{{2 - m}}{{m + 1}},\,\,\dfrac{{5m + 2}}{{m + 1}}} \right)$ is the point of intersection of lines $(1)$ and \[\left( 2 \right)\].

Given that, the point is at a distance of \[3\] units from $( - 1,2)$

By distance formula,

$\sqrt {{{\left( {\dfrac{{2 - m}}{{m + 1}} + 1} \right)}^2} + {{\left( {\dfrac{{5m + 2}}{{m + 1}} - 2} \right)}^2}}  = 3$

Square both sides,

${\left( {\dfrac{{2 - m + m + 1}}{{m + 1}}} \right)^2} + {\left( {\dfrac{{5m + 2 - 2m - 2}}{{m + 1}}} \right)^2} = {3^2}$

$ \Rightarrow \dfrac{9}{{{{(m + 1)}^2}}} + \dfrac{{9{m^2}}}{{{{(m + 1)}^2}}} = 9$

Divide the equation by \[9\],

$\dfrac{{1 + {m^2}}}{{{{(m + 1)}^2}}} = 1$

By cross multiplication,

$1 + {m^2} = {m^2} + 1 + 2m$

$ \Rightarrow 2\;m = 0$

$ \Rightarrow m = 0$

Therefore, the slope of the required line must be zero that is, the line must be parallel 

to the $x$-axis.

16. The hypotenuse of a right-angled triangle has its ends at the points $(1,3)$ and $( - 4,1)$. Find the equation of the legs (perpendicular sides) of the triangle which are parallel to the axes.

Ans: Consider ${\text{PQR}}$ as the right angles triangle where $\angle {\text{R}} = {90^\circ }$

Here, infinity such lines are present.

$m$ is the slope of ${\text{PR}}$

Then, the slope of ${\text{QR}} = \dfrac{{ - 1}}{m}$

Equation of ${\text{PR}}$is,

$y - 3 = m(x - 1)$

By cross multiplication,

$x - 1 = \dfrac{1}{{m(y - 3)}}$

Equation of ${\text{QR}}$is,

$y - 1 = \dfrac{{ - 1}}{{m(x + 4)}}$

By cross multiplication

$x + 4 =  - m(y - 1)$

If $m = 0$,

$y - 3 = 0,\,\,x + 4 = 0$

If $m = \infty $,

$x - 1 = 0,\,\,y - 1 = 0$ 

That is, $x = 1,\,\,y = 1$

Therefore, the equation of the legs (perpendicular sides) of the triangle is $x = 1,\,\,y = 1$.

17. Find the image of the point $(3,8)$ with respect to the line $x + 3y = 7$ assuming the line to be a plane mirror.

Ans: Given that,

$x + 3y = 7 \to (1)$

Consider \[{\text{B}}\left( {a,{\text{ }}b} \right)\]as the image of point ${\text{A}}(3,8)$

So line \[\left( 1 \right)\]is perpendicular bisector of ${\text{AB}}$.

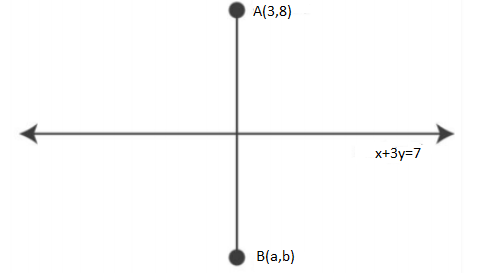
Slope of ${\text{AB}} = \dfrac{{b - 8}}{{a - 3}}$

Slope of line $(1) =  - \dfrac{1}{3}$

Line \[\left( 1 \right)\] is perpendicular to ${\text{AB}}$

Then,

$\left( {\dfrac{{b - 8}}{{a - 3}}} \right) \times \left( { - \dfrac{1}{3}} \right) =  - 1$

$ \Rightarrow \dfrac{{b - 8}}{{3a - 9}} = 1$

By cross multiplication,

$b - 8 = 3a - 9$

$3a - b = 1 \to (2)$

We know,

Mid-point of ${\text{AB}} = \left( {\dfrac{{a + 3}}{2},\,\,\dfrac{{b + 8}}{2}} \right)$

So the mid-point of line segment ${\text{AB}}$ will satisfy line \[\left( 1 \right)\].

From equation \[\left( 1 \right)\],

$\left( {\dfrac{{a + 3}}{2}} \right) + 3\left( {\dfrac{{b + 8}}{2}} \right) = 7$

By further calculation,

$a + 3 + 3\;b + 24 = 14$

On further simplification,

$a + 3b =  - 13 \to (3)$

Solve equations \[\left( 2 \right)\] and \[\left( 3 \right)\],

$a =  - 1$ and $b =  - 4$

Therefore, the image of the given point for the given line is $( - 1, - 4)$.

18. If the lines $y = 3x + 1$ and $2y = x + 3$ are equally indicated to the line $y = mx + 4$, find the value of $m$.

Ans: The equation of the given lines are ${\text{y}} = 3{\text{x}} + 1$

$2y = x + 3 \to (2)$

\[y = mx + 4 \to (3)\]

Slope of line\[\left( 1 \right)\] is  ${m_1} = 3$

Slope of line $(2)\,\,{\text{is}}\,\,{m_2} = \dfrac{1}{2}$

Slope of line $(3)\,\,{\text{is}}\,\,{m_3} = m$

We know that the lines \[\left( 1 \right)\] and \[\left( 2 \right)\] are equally inclined to line \[\left( 3 \right)\] which means that the angle between lines \[\left( 1 \right)\] and \[\left( 3 \right)\]equals the angle between lines $(2)$ and \[\left( 3 \right)\].

$\left| {\dfrac{{{m_1} - {m_3}}}{{1 + {m_1}{m_3}}}} \right| = \left| {\dfrac{{{m_2} - {m_3}}}{{1 + {m_2}{m_3}}}} \right|$

Substitute the values,

$\left| {\dfrac{{3 - m}}{{1 + 3m}}} \right| = \left| {\dfrac{{\dfrac{1}{2} - m}}{{1 + \dfrac{1}{2}m}}} \right|$

Take LCM

$\left| {\dfrac{{3 - m}}{{1 + 3m}}} \right| = \left| {\dfrac{{1 - 2m}}{{m + 2}}} \right|$

It can be written as,

$\dfrac{{3 - m}}{{1 + 3m}} =  \pm \left( {\dfrac{{1 - 2m}}{{m + 2}}} \right)$

Here,

$\dfrac{{3 - m}}{{1 + 3m}} = \dfrac{{1 - 2m}}{{m + 2}}$ or $\dfrac{{3 - m}}{{1 + 3m}} =  - \left( {\dfrac{{1 - 2m}}{{m + 2}}} \right)$

If $\dfrac{{3 - m}}{{1 + 3m}} = \dfrac{{1 - 2m}}{{m + 2}}$

By cross multiplication,

$(3 - m)(m + 2) = (1 - 2\;m)(1 + 3\;m)$

$ \Rightarrow  - {m^2} + m + 6 = 1 + m - 6{m^2}$

$ \Rightarrow 5{m^2} + 5 = 0$

Divide the equation by $5$

$ \Rightarrow {m^2} + 1 = 0$

$ \Rightarrow m = \sqrt { - 1} $, which is not real.

Therefore, this case is not possible.

If $\dfrac{{3 - m}}{{1 + 3m}} =  - \left( {\dfrac{{1 - 2m}}{{m + 2}}} \right)$

By cross multiplication,

$(3 - m)(m + 2) =  - (1 - 2\;m)(1 + 3\;m)$

$ \Rightarrow  - {m^2} + m + 6 =  - \left( {1 + m - 6\;{m^2}} \right)$

$ \Rightarrow 7{m^2} - 2m - 7 = 0$

Here we get,

$m = \dfrac{{2 \pm \sqrt {4 - 4(7)( - 7)} }}{{2(7)}}$

$m = \dfrac{{2 \pm 2\sqrt {1 + 49} }}{{14}}$

Rewrite as,

$m = \dfrac{{1 \pm 5\sqrt 2 }}{7}$

Thus, the required value of $m$ is $\dfrac{{1 \pm 5\sqrt 2 }}{7}$.

19. If the sum of the perpendicular distance of a variable point ${\text{P}}(x,y)$ from the lines $x + y - 5 = 0$ and $3x - 2y + 7 = 0$ is always \[10.\] Show that ${\text{P}}$ must move on a line.

Ans: Given that,

$x + y - 5 = 0 \to (1)$

$3x - 2y + 7 = 0 \to (2)$

Here the perpendicular distances of ${\text{P}}(x,y)$ from lines \[\left( 1 \right){\text{ and }}\left( 2 \right)\]are written as,

${d_1} = \dfrac{{|x + y - 5|}}{{\sqrt {{{(1)}^2} + {{(1)}^2}} }}$ and ${d_2} = \dfrac{{|3x - 2y + 7|}}{{\sqrt {{{(3)}^2} + {{( - 2)}^2}} }}$

Now, ${d_1} = \dfrac{{|x + y - 5|}}{{\sqrt 2 }}$ and ${d_2} = \dfrac{{|3x - 2y + 7|}}{{\sqrt {13} }}$

We know that ${d_1} + {d_2} = 10$

Substitute the values,

$\dfrac{{|x + y - 5|}}{{\sqrt 2 }} + \dfrac{{|3x - 2y + 7|}}{{\sqrt {13} }} = 10$

$ \Rightarrow \sqrt {13} |x + y - 5| + \sqrt 2 |3x - 2y + 7| - 10\sqrt {26}  = 0$

It can be written as,

$\sqrt {13} (x + y - 5) + \sqrt 2 (3x - 2y + 7) - 10\sqrt {26}  = 0$

Assume $(x + y - 5)$ and $(3x - 2y + 7)$ are positive,

$\sqrt {13} x + \sqrt {13} y - 5\sqrt {13}  + 3\sqrt 2 x - 2\sqrt 2 y + 7\sqrt 2  - 10\sqrt {26}  = 0$

Take out the common terms,

$x(\sqrt {13}  + 3\sqrt 2 ) + y(\sqrt {13}  - 2\sqrt 2 ) + (7\sqrt 2  - 5\sqrt {13}  - 10\sqrt {26} ) = 0$, which is the equation of a line.

Similarly, we can find the equation of the line for any signs of $(x + y - 5)$ and 

$(3x - 2y + 7)$.

Therefore, point ${\text{P}}$ must move on a line.

20. Find the equation of the line which is equidistant from parallel lines $9x + 6y - 7 = 0$ and $3x + 2{\text{y}} + 6 = 0.$

Ans: The equation of the given lines are $9x + 6y - 7 = 0 \to (1)$

$3x + 2y + 6 = 0 \to (2)$

Consider ${\text{P}}(h,k)$ be the arbitrary point that is equidistant from lines \[\left( 1 \right){\text{ and }}\left( 2 \right)\].

Here, the perpendicular distance of ${\text{P}}(h,k)$ from line $(1)$ is,

${d_1} = \dfrac{{|9h + 6k - 7|}}{{{{(9)}^2} + {{(6)}^2}}} $

$= \dfrac{{|9h + 6k - 7|}}{{\sqrt {117} }} $

$= \dfrac{{|9h + 6k - 7|}}{{3\sqrt {13} }} $

Similarly, the perpendicular distance of ${\text{P}}(h,k)$ from line \[\left( 2 \right)\] is,

${d_2} = \dfrac{{|3h + 2k + 6|}}{{\sqrt {{{(3)}^2} + {{(2)}^2}} }} $

$= \dfrac{{|3h + 2k + 6|}}{{\sqrt {13} }} $

We know that ${\text{P}}(h,k)$ is equidistant from lines \[(1){\text{ and }}\left( 2 \right)\]

That is, ${d_1} = {d_2}$

Substitute the values,

$\dfrac{{|9h + 6k - 7|}}{{3\sqrt {13} }} = \dfrac{{|3h + 2k + 6|}}{{\sqrt {13} }}$

$ \Rightarrow |9h + 6k - 7| = 3|3h + 2k + 6|$

$ \Rightarrow |9h + 6k - 7| =  \pm 3(3h + 2k + 6)$

Now, $9h + 6k - 7 = 3(3h + 2k + 6)$ or $9h + 6k - 7 =  - 3(3h + 2k + 6)$

$ \Rightarrow 9h + 6k - 7 = 3(3h + 2k + 6)$ is not possible as,

$9h + 6k - 7 = 3(3h + 2k + 6)$

$ - 7 = 18$ ,which is wrong

We have,

$9h + 6k - 7 =  - 3(3h + 2k + 6)$

By multiplication

$9h + 6k - 7 =  - 9h - 6k - 18$

$ \Rightarrow 18h + 12k + 11 = 0$

Therefore, the required equation of the line is $18x + 12y + 11 = 0$.

21. A ray of light passing through the point $(1,2)$ reflects on the $x$-axis at point ${\text{A}}$ and the reflected ray passes through the point $(5,3)$. Find the coordinates of ${\text{A}}$.

Ans:

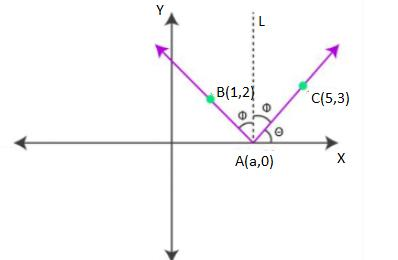
Consider the coordinates of point ${\text{A}}$ as $(a,0)$

Construct a line \[\left( {{\text{AL}}} \right)\]which is perpendicular to the $x$-axis

Here, the angle of incidence is equal to the angle of reflection.

That is,

$\angle {\text{BAL}} = \angle {\text{CAL}} = \emptyset $

$\angle {\text{CAX}}$ $ = \theta $

It can be written as,

$\angle {\text{OAB}} = {180^\circ } - (\theta  + 2\phi ) = {180^\circ } - \left[ {\theta  + 2\left( {{{90}^\circ } - \theta } \right)} \right]$

$ = {180^\circ } - \theta  - {180^\circ } + 2\theta $

$ = \theta $

Now, $\angle {\text{BAX}} = {180^\circ } - \theta $

Slope of line ${\text{AC}} = \dfrac{{3 - 0}}{{5 - a}}$

$\tan \theta  = \dfrac{3}{{5 - a}} \to (1)$

Slope of line ${\text{AB}} = \dfrac{{2 - 0}}{{1 - a}}$

$\tan \left( {{{180}^\circ } - \theta } \right) = \dfrac{2}{{1 - a}}$

$ \Rightarrow  - \tan \theta  = \dfrac{2}{{1 - a}}$

$ \Rightarrow \tan \theta  = \dfrac{2}{{a - 1}}$

From equations \[\left( 1 \right){\text{ and }}\left( 2 \right)\],

$\dfrac{3}{{5 - a}} = \dfrac{2}{{a - 1}}$

By cross multiplication,

$3a - 3 = 10 - 2a$

$ \Rightarrow a = \dfrac{{13}}{5}$

Therefore, the coordinates of point ${\text{A}}$ are $\left( {\dfrac{{13}}{5},0} \right)$.

22. Prove that the product of the lengths of the perpendiculars drawn from the points $\left( {\sqrt {{a^2} - {b^2}} ,0} \right)$ and $\left( { - \sqrt {{a^2} - {b^2}},0} \right)$ to the line $\dfrac{x}{a}\cos \theta  + \dfrac{y}{b}\sin \theta  = 1$ is ${b^2}$.

Ans: Given that,

$\dfrac{x}{a}\cos \theta  + \dfrac{y}{b}\sin \theta  = 1$

Rewrite as,

$bx\cos \theta  + ay\sin \theta  - ab = 0 \to (1)$

Here, the length of the perpendicular from point $\left( {\sqrt {{a^2} - {b^2}} ,0} \right)$ to line \[\left( 1 \right)\] is,   

${p_1} = \dfrac{{\left| {b\cos \theta \left( {\sqrt {{a^2} - {b^2}} } \right) + a\sin \theta (0) - ab} \right|}}{{\sqrt {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } }} $

$= \dfrac{{\left| {b\cos \theta \sqrt {{a^2} - {b^2}}  - ab} \right|}}{{\sqrt {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } }} $

Similarly, the length of the perpendicular from point $\left( { - \sqrt {{a^2} - {b^2}} ,0} \right)$ to line $(2)$ is,

${p_2} = \dfrac{{\left| {b\cos \theta \left( { - \sqrt {{a^2} - {b^2}} } \right) + a\sin \theta (0) - ab} \right|}}{{\sqrt {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } }} $

$= \dfrac{{\left| {b\cos \theta \sqrt {{a^2} - {b^2}}  + ab} \right|}}{{\sqrt {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } }} $

Multiply equations \[\left( {\text{2}} \right){\text{ and }}\left( {\text{3}} \right),\]

$ = \dfrac{{\left| {\left( {b\cos \theta \sqrt {{a^2} - {b^2}}  - ab} \right)\left( {b\cos \theta \sqrt {{a^2} - {b^2}}  + ab} \right)} \right|}}{{\left( {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } \right)}}$

From the formula,

$ = \dfrac{{\left| {{{\left( {b\cos \theta \sqrt {{a^2} - {b^2}} } \right)}^2} - {{(ab)}^2}} \right|}}{{\left( {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } \right)}}$

Square the numerator,

$ = \dfrac{{\left| {{b^2}{{\cos }^2}\theta \left( {{a^2} - {b^2}} \right) - {a^2}{b^2}} \right|}}{{\left( {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } \right)}}$

Expand using the formula,

$ = \dfrac{{\left| {{a^2}{b^2}{{\cos }^2}\theta  - {b^4}{{\cos }^2}\theta  - {a^2}{b^2}} \right|}}{{{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta }}$

Take out the common terms,

$ = \dfrac{{{b^2}\left| {{a^2}{{\cos }^2}\theta  - {b^2}{{\cos }^2}\theta  - {a^2}} \right|}}{{{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta }}$

$ = \dfrac{{{b^2}\left| {{a^2}{{\cos }^2}\theta  - {b^2}{{\cos }^2}\theta  - {a^2}{{\sin }^2}\theta  - {a^2}{{\cos }^2}\theta } \right|}}{{{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta }}$

Here, ${\sin ^2}\theta  + {\cos ^2}\theta  = 1$ (trigonometric identity)

$ = \dfrac{{{b^2}\left| { - \left( {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } \right)} \right|}}{{{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta }}$

$ = \dfrac{{{b^2}\left( {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } \right)}}{{\left( {{b^2}{{\cos }^2}\theta  + {a^2}{{\sin }^2}\theta } \right)}}$

Cancel common terms,

$ = {b^2}$

Hence, proved that the product of the lengths of the perpendiculars drawn from the points $\left( {\sqrt {{a^2} - {b^2}},0} \right)$ and $\left( { - \sqrt {{a^2} - {b^2}} ,0} \right)$ to the line $\dfrac{x}{a}\cos \theta  + \dfrac{y}{b}\sin \theta  = 1$ is ${b^2}$.

23. A person standing at the junction (crossing) of two straight paths represented by the equation $2x - 3y + 4 = 0$ and $3x + 4y - 5 = 0$ wants to reach the path whose equation is $6x - 7y + 8 = 0$in the last time. Find the equation of the path that he should follow.

Ans: Given that,

$2x - 3y + 4 = 0 \to (1)$

$3x + 4y - 5 = 0 \to (2)$

$6x - 7y + 8 = 0 \to (3)$ 

Here, the person is standing at the junction of the paths represented by lines 

\[\left( {\text{1}} \right){\text{ and }}\left( {\text{2}} \right){\text{.}}\]

Solve equations \[\left( {\text{1}} \right){\text{ and }}\left( {\text{2}} \right),\]

$x = \dfrac{{ - 1}}{{17}}$ and $y = \dfrac{{22}}{{17}}$

Thus, the person is standing at point $\left( {\dfrac{{ - 1}}{{17}},\dfrac{{22}}{{17}}} \right)$.

It is known that the person can reach path \[\left( 3 \right)\]in the least time if he walks along the perpendicular line to (3) from point $\left( {\dfrac{{ - 1}}{{17}},\dfrac{{22}}{{17}}} \right)$

Here, the slope of the line $(3) = \dfrac{6}{7}$

Now, the slope of the line perpendicular to line $(3) = \dfrac{1}{{\left( {\dfrac{6}{7}} \right)}} = \dfrac{{ - 7}}{6}$

So the equation of line passing through point $\left( {\dfrac{{ - 1}}{{17}},\dfrac{{22}}{{17}}} \right)$and having a slope of $\dfrac{{ - 7}}{6}$ is,

$\left( {y - \dfrac{{22}}{{17}}} \right) =  - \dfrac{7}{6}\left( {x + \dfrac{1}{{17}}} \right)$

$ \Rightarrow 6(17y - 22) =  - 7(17x + 1)$

By multiplication,

$102y - 132 =  - 119x - 7$

$ \Rightarrow 119x + 102y = 125$

Therefore, the path that the person should follow is $119x + 102y = 125$.

Conclusion

Complete exercise in understanding Straight Line concepts is provided by the NCERT Class 11 Maths Chapter 9 Miscellaneous Solutions. Their knowledge of equations, angles, and point-to-point distances is improved by these types of exercises, which also help them improve their analysis skills. Regular practice improves student's confidence in solving challenging problems, makes them ready for assessments, and creates an effective basis for their future studies in math.

Class 11 Maths Chapter 9: Exercises Breakdown

CBSE Class 11 Maths Chapter 9 Other Study Materials

Chapter-Specific NCERT Solutions for Class 11 Maths

Given below are the chapter-wise NCERT Solutions for Class 11 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

Important Related Links for CBSE Class 11 Maths