Introduction to Factorization
Factors of a number is defined as the integers that completely and evenly divide the given number without leaving any remainder. Given a number, we can write it into a product of its factors. This is known as the factorisation of a number. The factors are the numbers which are always smaller than or equal to the given number and divided the number exactly.
Definition of Factor
A factor of a number is another number that divides the given number without leaving any remainder. We can add finite copies of a factor together to get the original number. For example, 2 is divisible by 1 and 2. So, factors of 2 are 1 and 2.
How to Find Factors of 69?
Given the number 69, we know at least two factors of the number 1 and the number itself. So, two of the factors of 69 are 1 and 69. To find the remaining factors, we start dividing 69 by 2,3,4,… up to 68 (as the factors are always less than or equal to the given number). We find that 3 divides 69, and the quotient is 23.
So, 3 and 23 are the factors of 69. Next, we need to check up to 23 only because if we divide 69 by a number more than 23 it returns a quotient that must be less than 3, but 3 is the least prime that divides 69 evenly. After 3, we find that no other number divides 69 exactly. Hence, we get the factors of 69 as 1,3,23 and 69.
If we consider 69 as an integer, then the factors of 69 will include both positive and negative factors as: 1,-1,3,-3,23,-23,69,-69.
What are the Factors of 69?
Prime numbers have only two factors,i.e., 1 and the number itself. The factors of 69 are 1,3,23, and 69. Out of these, the prime numbers are 3 and 23. So, the prime factors of 69 are 3 and 23.
Considering 69 as an integer, the prime factors of 69 will be 3, 23.
Prime Factorization of 69
To find the prime factorisation of 69, find the prime factors of 69. Recall that Prime Factors are the numbers that have only two factors: 1 and the number itself. Out of 1,3,23,69, the prime numbers are 3 and 23.
So, the prime factors of 69 are 3,23 and 3×23=69.
Prime Factorization of 69 is 3×23.
We can do this in another way:
Start from 2(prime number). Is \[69\div 2\] a whole number? NO.
The next prime is 3. Is \[69\div 3\] a whole number? YES.
Next, do it for 23. Continue till we get 1 at the end.
Write 3 to the left of 69 and \[69 \div 3\], i.e., 23 below 69.
Again start from 2. Is \[23 \div 2\] a whole number? No.
The next prime number is 3. Is \[23 \div 3\] a whole number? No.
Since 23 is a prime number, 23 is divisible by 23.
Now, write the numbers in the left column in form of multiplication as \[69=3\times23\].
This is the prime factorization of 69.
If we consider 69 as an integer, then we can write the prime factorization of 69 as \[(-3)\times(-23)\].
Formula for Number of Factors
The prime factorization of a number is $x^a.y^b.z^c$. Where x,y,z are prime numbers, then number of factors=(a+1)(b+1)(c+1)
Prime Factorization of 69 Using Factor Tree
Factor trees are a way of expressing the factorization of a number in terms of its prime factors. It uses repeated division by prime numbers to get the prime factorization.
All the branches of the tree are split into factors. When the factors at the end are prime numbers, we stop, and the numbers at the end are prime factors. Writing them in multiplicative form gives the prime factorisation of 69.
We start dividing the number by prime numbers and write the number and the quotient as the tree branches. This process is repeated till we get all the prime numbers at the end.
This is represented as
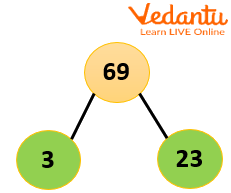
Tree diagram of 69
So, the prime factorisation of 69 is 3×23.
Factors of 69 in Pairs
To write all the factors of 69 in pairs, we see that
\[1\times 69=69\]
\[3\times23=69\]
\[23\times 3=69\]
\[69\times 1=69\]
So, writing the numbers on the left-hand side in pairs, we get (1,69),(3,23)are the factors of 69 in pairs.
Now considering the negative factors of 69.
\[-1\times (-69)=69\]
\[-3\times (-23)=69\]
\[-23\times (-3)=69\]
\[-69\times (-1)=69\]
So, writing the numbers on the left-hand side in pairs, we get (-1,-69),(-3,-23) are the factors of 69 in pairs.
Conclusion
In this topic page, we have learned about the factors of 69, all the factors of 69, its prime factorisation, prime factors of 69, and factor pairs of 69.
Key Features
To find the factors of 69 we can use a factor tree.
The factors of 69 are 1, 3, 23, 69, and their negative counterparts.
The factor pairs of 69 are \[1\times69\], \[3\times23\], \[-1\times(-69)\] and \[-3\times (-23)\].
List of Related articles
FAQs on Factors of 69
1. Is 69 composite or prime?
The factors of 69 are 1,3,23,69,-1,-3,-23,-69. So 69 has factors other than 1 and 69. Hence, 69 is a composite number.
2. Which are the prime factors of 69?
The prime factorization form of 69 is
3 | 69 |
23 | 23 |
1 |
The prime factors of 69 are 3 and 23.
3. Why is 1 a prime factor 69?
A prime number that divides 69 evenly is known as the prime factor of 69. 1 is not a prime number because a prime number has at least 2 factors but 1 has only one factor. Thus, 1 is not a prime factor of 69.
