




How to Find LCM of 3 Numbers Easily with Step-by-Step Solutions
The least common multiple (LCM) is the smallest positive integer that is divided by both a and b. Its official name is Least Common Multiple.
The LCM method is used to determine the least multiple of two or more numbers. Both of the numbers will divide the LCM. When performing any arithmetic operations involving fractions, such as addition and subtraction, LCM is utilized to make the denominators common. This method facilitates the simplification process.
What is LCM?
When the denominators of two fractions are different, LCM can also be used to add or subtract the fractions. The smallest positive integer that is divided by both a and b is known as the least common multiple (LCM) .A number that is a multiple of two or more other numbers is said to be a common multiple.
LCM with 3 Numbers:
LCM is represented as LCM for three integers a, b, and c. For instance, the smallest number that can be divided by all three integers is 60, which is the LCM of 12, 15, and 10. \[{\rm{LCM}}\left[ {12,15,10} \right]\] thus equals 60.
How to Calculate LCM of Three Numbers:
To find 3 Numbers LCM with Listing Multiples:
This is a very interesting process to How to Take the LCM of 3 Numbers:
List every multiple of three numbers until at least one of them appears on every list.
Find the number that appears on all of the lists and is the least.

LCM of 3 Numbers Formula(for 8, 4, 6)
Utilizing Prime Factorization, get the LCM of Three Numbers:
Make a list of each of the provided numbers' prime factors.
List all the prime numbers you've discovered, in order of how frequently they appear in the given numbers.
To find the Least Common Multiple, multiply the list of prime numbers.
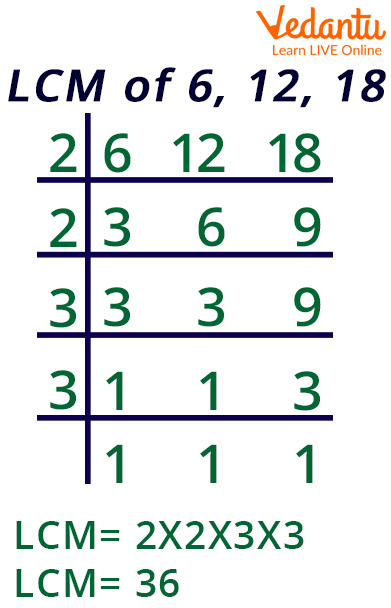
LCM of 6,12,18
Find LCM of Numbers Using Cake/ Ladder Method:
Put the three numbers in a row or cake pattern.
Bring the result into the following layer after dividing the integers in the layer by the given number that is equally divisible by all those numbers present.
Simply bring any non-divisible number down if it is present in the layer or row.
Divide the rows by prime numbers once more.
You are finished when there are no more numbers.
Then, multiply all the numbers together and you will get the LCM of required numbers.
Properties of LCM:
PROPERTY 1 : LCM obeys Associative Property
\[{\rm{LCM}}\left[ {c,d} \right] = {\rm{LCM}}\left[ {d,c} \right]\]
PROPERTY 2 : LCM obeys Commutative Property
\[{\rm{LCM}}\left[ {a,b,c} \right] = {\rm{LCM}}\left[ {{\rm{LCM}}\left[ {a,b} \right],c} \right] = {\rm{LCM}}\left[ {a,{\rm{LCM}}\left[ {b,c} \right]} \right]\]
PROPERTY 3 : LCM obeys Distributive Property
\[{\rm{LCM}}\left[ {da,db,dc} \right] = d \times {\rm{LCM}}\left[ {a,b,c} \right]\]
Conclusion
LCM can be used to add or subtract two fractions when their respective denominators are different. The least common multiple (LCM) is the smallest positive integer that is divided by both a and b. (LCM).
Solved Example :
Example 1 : Find \[{\rm{LCM}}\left[ {6,7,21} \right]\] by listing Multiples.
Solution : Given digits 6, 7, and 21
There are six multiples: 6, 12, 18, 24, 30, 36, 42, 48, 54, and 60
7 is a multiple of 14, 21, 28, 35, 42, 49, and 56.
21 is a multiple of 21, 42, and 63.
According to the definition, the least common multiple [LCM] of all three integers is the smallest number.
Thus, the LCM of 6, 7, and 21 is 42.
Example 2 : Find LCM of 12, 24, 30 using Prime Factorization Method?
Solution : 12's prime factorization is \[2 \times 2 \times 3\]
24's prime factorization is \[2 \times 2 \times 2 \times 2 \times 3\]
prime factorization of 30 will be \[2 \times 3 \times 5\]
Make a note of the often occurring prime numbers for the provided numbers, then multiply them.
\[ = 2 \times 2 \times 2 \times 3 \times 5\]
\[ = 120\]
Thus, its LCM of given numbers is 120.
Example 3 : Find the LCM(10, 12, 15) using the Cake/ Ladder Method.
Solution : Numbers given are 10, 12, and 15.

LCM of 10,12,15 by Cake/Ladder Method
Using a Cake and Ladder
To locate LCM From top to bottom, multiply all the prime integers, i.e.
\[2 \times 3 \times 5 \times 1 \times 2 \times 1 = 60\]
LCM(10, 12, 15) is therefore 60.
FAQs on LCM with 3 Numbers: Guide, Methods & Practice
1. How to find LCM with 3 numbers?
To find the LCM (Least Common Multiple) of three numbers, follow these steps:
- First, find the LCM of the first two numbers.
- Next, calculate the LCM of the result from step one and the third number.
$\mathrm{LCM}(a, b, c) = \mathrm{LCM}(\mathrm{LCM}(a, b),\ c)$
At Vedantu, students can master this concept through live sessions and interactive worksheets for efficient step-by-step learning.
2. What is the LCM of 24, 36 and 40?
To find the LCM of 24, 36, and 40, perform their prime factorization:
- 24 = $2^3 \times 3$
- 36 = $2^2 \times 3^2$
- 40 = $2^3 \times 5$
$\text{LCM} = 2^3 \times 3^2 \times 5 = 8 \times 9 \times 5 = 360$
Using methods explained in Vedantu online classes, students can approach these calculations systematically.
3. What is the LCM of 40 48 and 45?
Let's determine the LCM of 40, 48, and 45 using prime factorization:
- 40 = $2^3 \times 5$
- 48 = $2^4 \times 3$
- 45 = $3^2 \times 5$
Vedantu’s expert tutors break down such problems for easy understanding through stepwise teaching.
4. What is the LCM of 24, 48 and 60?
To find the LCM of 24, 48, and 60, consider each number’s prime factors:
- 24 = $2^3 \times 3$
- 48 = $2^4 \times 3$
- 60 = $2^2 \times 3 \times 5$
Vedantu offers video lessons and exercises that help learners grasp such LCM calculations efficiently.
5. What are the common methods to calculate the LCM of three numbers?
There are several methods to efficiently calculate the LCM of three numbers:
- Prime factorization (finding highest powers for each prime factor)
- Listing multiples (listing out some multiples of each number to find the first common one)
- Division method (dividing by prime numbers across all three numbers)
6. How does finding the LCM help in solving real-life math problems?
Finding the LCM is important in various real-life applications, such as:
- Scheduling events (to find when they coincide)
- Solving problems involving repeating patterns
- Working with fractions (finding common denominators)
7. Can Vedantu help students practice LCM questions for competitive exams?
Yes, Vedantu provides dedicated practice resources, mock tests, and personalized guidance for topics like LCM with three numbers in competitive exams. Students receive expert mentoring on solving complex LCM questions faster and more accurately.
8. What is the difference between LCM and HCF when working with three numbers?
LCM (Least Common Multiple) is the smallest number divisible by all three numbers. HCF (Highest Common Factor) is the greatest number that divides all three numbers. Both are essential in understanding factors and multiples, a core topic covered extensively in Vedantu’s math curriculum.
9. Are there shortcuts to finding the LCM of large numbers?
Yes, there are shortcuts and tips for quickly finding the LCM of larger numbers, such as:
- Using prime factorization for efficiency
- Breaking complex numbers into smaller factors
- Utilizing division tables and patterns























