Descending Order in Fraction Explained with Methods and Examples

An element of a whole is a fraction. The number is represented mathematically as a quotient, where the numerator and denominator are divided. Both are integers in a simple fraction. A fraction appears in the numerator or denominator of a complex fraction.

Before being ordered in ascending and descending order, the fractions might first be expressed as similar fractions. Fractions having the same denominator are said to be like fractions. To arrange the fractions in order, we shall change them to like fractions.

Decreasing Order of Height for Different Animals

What are Like and Unlike Fractions?

Based on the denominators, there are two basic categories of fractions: like fractions and unlike fractions. Like fractions are those in which two or more fractions have the same denominator, and unlike fractions are those in which two or more fractions have distinct denominators. For example, \[\frac{1}{2}\] and \[\frac{3}{2}\] are like fractions and \[\frac{1}{9}\] and \[\frac{3}{7}\] are unlike fractions.

Steps to Convert the Fractions in Descending Order:

There are two ways we can arrange the fraction in descending order.

• The first process involves comparing each fraction's denominator to see if they are equal before arranging and comparing the numerators.

• The second method is converting the given fractions to decimals before comparison and arrangement.

In the first method, all the specified fractions' denominators will be checked. Simply compare the numerator and arrange fractions based on it if all the denominators are equal. However, if the denominators are not all equal, use the LCM to make them all equal, then check the numerator, and finally arrange the terms in descending order (fraction greatest to least calculator).

Comparison of Like Fractions:

Since the denominators of like fractions are the same, we can compare like fractions by comparing their numerators. If the numerator is larger, the fraction is larger; when it is smaller, the fraction is smaller.

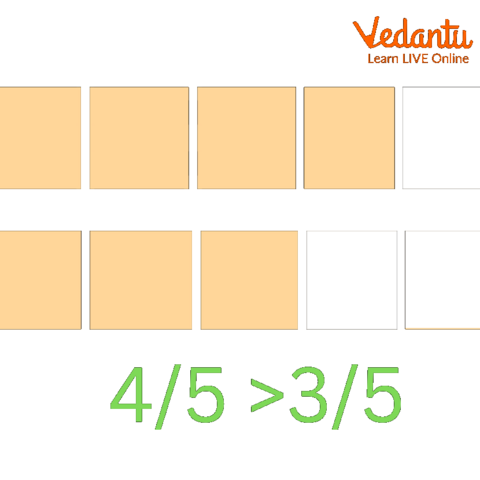
Comparison of Like Fractions

Solved Examples:(Order Fractions Worksheet)

Example 1: Arrange the following fractions in descending order: \[\frac{1}{2}\], \[\frac{3}{4}\], \[\frac{7}{8}\], and \[\frac{5}{{12}}\].

Ans: To make the denominators of the fractions the same (like fractions), we should first determine the L.C.M. of the denominators.

LCM for 2, 4, 8, and 12 will be 24.

Due to the fact that \[24 \div 2 = 12\], \[\frac{1}{2} = \frac{{1 \times 12}}{{2 \times 24}} = \frac{{12}}{{24}}\].

Because \[24 \div 10 = 6\], \[\frac{3}{4} = \frac{{3 \times 6}}{{4 \times 6}} = \frac{{18}}{{24}}\].

Since \[24 \div 20 = 3\], \[\frac{7}{8} = \frac{{7 \times 3}}{{8 \times 3}} = \frac{{21}}{{24}}\].

Due to the fact that \[24 \div 20 = 3\], \[\frac{5}{{12}} = \frac{{5 \times 2}}{{12 \times 2}} = \frac{{10}}{{24}}\].

The like fractions \[\frac{{12}}{{24}}\], \[\frac{{18}}{{24}}\], \[\frac{{21}}{{24}}\], and \[\frac{{10}}{{24}}\] are now compared.

Numerators are compared, and we discover that \[21 > 18 > 12 > 10\]

Therefore, \[\frac{7}{8} > \frac{3}{4} > \frac{1}{2} > \frac{5}{{12}}\] or \[\frac{{21}}{{24}} > \frac{{18}}{{24}} > \frac{{12}}{{24}} > \frac{{10}}{{24}}\]

The fractions are arranged in descending order as follows: \[\frac{7}{8} > \frac{3}{4} > \frac{1}{2} > \frac{5}{{12}}\].

Example 2: Arrange the following fractions in descending order:

\[\frac{1}{2}\], \[\frac{2}{3}\], \[\frac{7}{{12}}\], \[\frac{5}{6}\], \[\frac{1}{4}\].

Ans: Determine all of the fractions' denominators first. The denominators in this situation are 2, 3, 12, 6, and 4.

Determine the denominators' least common multiple. Check whether the other denominators are factors of the calculated L.C.M. by looking at the L.C.M. of two numbers at once.

12 is the least frequent denominator among the following: 2, 3, 12, 6, and 4.

Rewriting each fraction as an analogous fraction with the denominator 12 comes next: \[\frac{1}{2} \times \frac{6}{6} = \frac{6}{{12}}\].

\[\frac{2}{3} \times \frac{4}{4} = \frac{8}{{12}}\]

\[\frac{7}{{12}} \times \frac{1}{1} = \frac{7}{{12}}\]

\[\frac{5}{6} \times \frac{2}{2} = \frac{{10}}{{12}}\]

\[\frac{1}{4} \times \frac{3}{3} = \frac{3}{{12}}\]

The final solution now becomes \[\frac{5}{6}\] , \[\frac{2}{3}\] , \[\frac{7}{{12}}\] , \[\frac{1}{4}\] by comparing the numerators of like fractions.

Example 3: List the following fractions in descending order.

\[\frac{{24}}{6}\] ,\[\frac{{48}}{6}\],\[\frac{{12}}{6}\],\[\frac{{55}}{6}\].

Ans: The above fractions can be considered fractions because they have the same denominators. So, we will get our required answer by comparing the numerators.

Thus,

Its order will be: \[\frac{{55}}{6}\],\[\frac{{48}}{6}\],\[\frac{{24}}{6}\],\[\frac{{12}}{6}\]

Conclusion:

It is possible that the fractions are first stated as similar fractions before being arranged in ascending and descending order. It is stated that fractions with the same denominator are similar to one another. We will alter the fractions to like fractions in order to arrange them in numerical order.