Cyclic Quadrilateral Complete Guide with Theorems and Proofs

To understand what a cyclic quadrilateral is, we should know what quadrilaterals are. A quadrilateral is called a closed, two-dimensional geometrical figure with four sides, four angles, and four vertices. Square, rectangle, rhombus, and trapezium are a few examples of quadrilaterals.

A four-sided shape that a circle can encircle is a cyclic quadrilateral. The quadrilateral ABCD in the given figure is cyclic because each of its four vertices—A, B, C, and D—lies on the circle's circumference. The cyclic quadrilateral, its definition, theorems, properties, angles, and examples of cyclic quadrilateral problems with solutions are all covered in detail in this article.

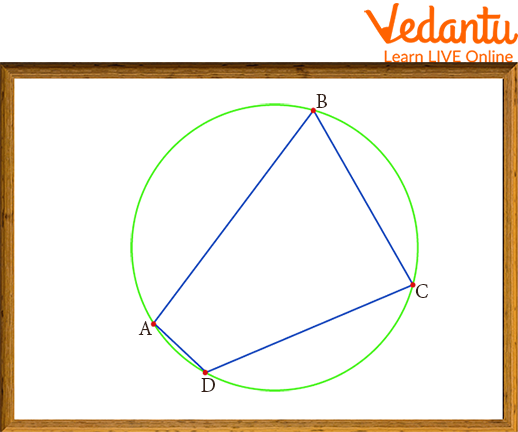
An Inscribed or Cyclic Quadrilateral

Properties of Cyclic Quadrilateral

Here some properties of cyclic quadrilateral angles are listed below:

1. The total of either pair of opposite angles in a cyclic quadrilateral is supplementary, i.e. 180 degrees.

2. For a quadrilateral to be cyclic, its opposing angles must be supplementary to one another.

3. In a cyclic quadrilateral, the sum of the products of its two pairs of opposite sides equals the product of the diagonals.

4. In a cyclic quadrilateral exterior angle is equal to the interior opposite angle if only one side is produced.

Angles of Cyclic Quadrilateral

Let's assume that $A B C D$ is quadrilateral, whose vertices are on a circle. Let's demonstrate a cyclic quadrilateral whose opposite angles are supplementary.

Join the circle's centre $O$ to each vertex. We see four radii $O A, O B, O C$ and $O D$, giving rise to four isosceles triangles $\triangle O A B, \triangle O B C, \triangle O C D$ and $\triangle O D A$. We already know that the sum of the angels surrounding the circle's centre is $360^{\circ}$ circles and that the sum of the angles in each triangle is $180^{\circ}$ circles.

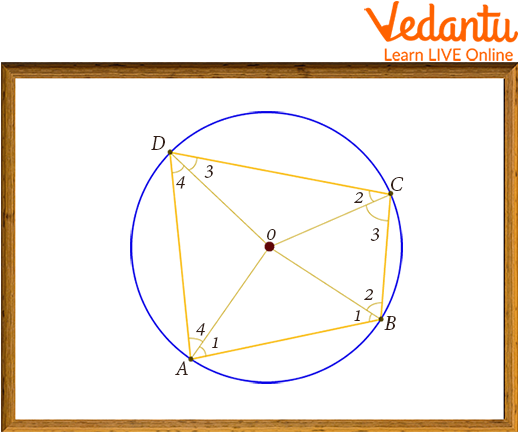
Cyclic Quadrilateral ABCD

Therefore, we get from the figure:

$2(\angle 1+\angle 2+\angle 3+\angle 4)+$ Angle at centre $\mathrm{O}=4 \times 180^{\circ}$

$2(\angle 1+\angle 2+\angle 3+\angle 4)+360^{\circ}=720^{\circ}$

$(\angle 1+\angle 2+\angle 3+\angle 4)=180^{\circ}$

We now interpret this as:

1. $(\angle 1+\angle 2)+(\angle 3+\angle 4)=180^{\circ}$ (Sum of opposite angles of a cyclic quadrilateral)

2. $(\angle 1+\angle 4)+(\angle 2+\angle 3)=180^{\circ}$ (Sum of opposite angles of a cyclic quadrilateral)

Cyclic Quadrilateral Theorems

There are three main theorems on the cyclic quadrilateral. These are discussed below.

Theorem 1: “In a cyclic quadrilateral, the sum of either pair of opposite angles is supplementary.”

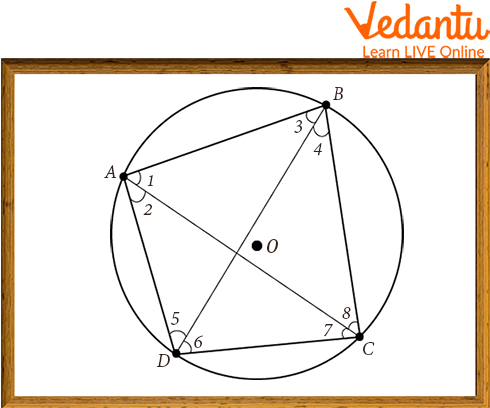
Cyclic Quadrilateral ABCD

Proof: Given: ABCD is a cyclic quadrilateral of a circle with a centre at $O$

To prove:

$\angle B A D+\angle B C D=180^{\circ}$

$\angle A B C+\angle A D C=180^{\circ}$

$A B$ is the chord of the circle

$\angle 5=\angle 8 \ldots$ (1) (Angles in the same segment are equal)

$\mathrm{BC}$ is the chord of the circle

$\angle 1=\angle 6 \ldots$ (2) (Angles in the same segment are equal)

$C D$ is the chord of the circle

$\angle 2=\angle 4 \ldots$ (3) (Angles in the same segment are equal)

$A D$ is the chord of the circle

$\angle 7=\angle 3 \ldots$ (4) (Angles in the same segment are equal)

By angle sum property of a quadrilateral

$\angle \mathrm{A}+\angle \mathrm{B}+\angle \mathrm{C}+\angle \mathrm{D}=360^{\circ}$

$\angle 1+\angle 2+\angle 3+\angle 4+\angle 7+\angle 8+\angle 5+\angle 6=360^{\circ}$

$(-1+\angle 2+\angle 7+\angle 8)+(-3+\angle 4+\angle 5+\angle 6)=360^{\circ}$

$(-1+\angle 2+\angle 7+\angle 8)+(\angle 7+\angle 2+\angle 8+\angle 1)=360^{\circ}$

From equation

$(1),(2),(3)$, and (4)

$2(\angle 1+\angle 2+\angle 7+\angle 8)=360^{\circ}$

$(\angle 1+\angle 2+\angle 7+\angle 8)=180^{\circ}$

$\angle B A D+\angle B C D=180^{\circ}$

Similarly,

$\angle A B C+\angle A D C=180^{\circ}$

Hence proved.

Theorem 2: Ptolemy’s Theorem: “If there is a quadrilateral inscribed in a circle, then the product of the diagonals is equal to the sum of the product of its two pairs of opposite sides.”

If ABCD is a cyclic quadrilateral,

AB and CD, and AD and BC are opposite sides.

AC and BD are the diagonals.

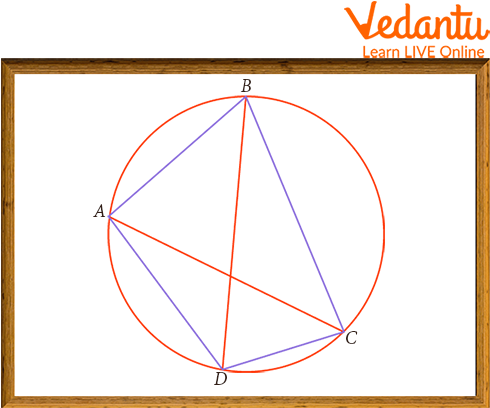
Cyclic Quadrilateral (Ptolemy's Theorem )

(AB×CD)+(AD×BC)=AC×BD

(AB×CD)+(AD×BC)=AC×BD

Theorem 3: “If one side of a cyclic quadrilateral is produced, then the exterior angle is equal to the interior opposite angle.”

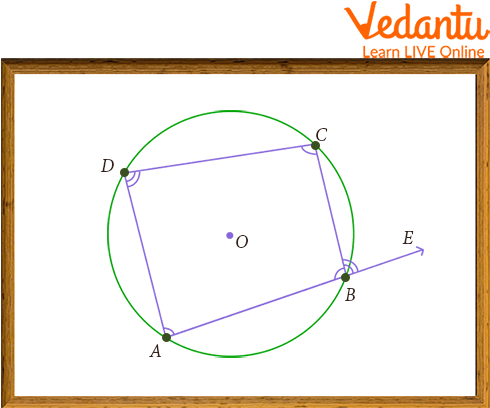
Cyclic Quadrilateral

To prove:

$\angle CBE=\angle ADC$

$\angle CBE=\angle ADC$

Proof:

Let the side $AB$ of the cyclic quadrilateral $ABCD$ be extended to $E$.

Here, $\angle ABC$ and $\angle CBE$ are linear pairs, their sum is $180 \circ$, and the angles $\angle ABC$ and $\angle ADC$ are the opposite angles of a cyclic quadrilateral, and their sum is also $180^{\circ}$

From this,

$\angle ABC+\angle CBE=\angle ABC+\angle ADC$

and finally, we get

$\angle CBE=\angle ADC$.

Similarly, we can prove it from all angles.

Solved Examples

Example 1: If ABCD is a cyclic quadrilateral, find the value of x and y.

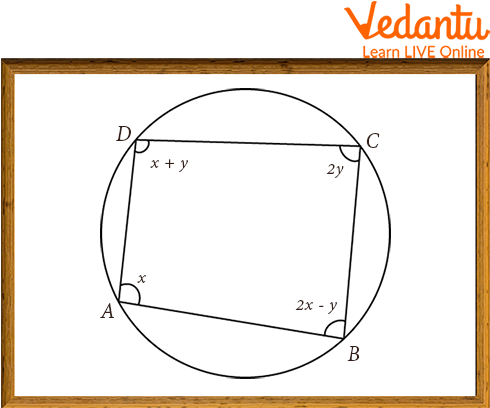
Cyclic Quadrilateral

Solution: We know that the sum of opposite angles of a cyclic quadrilateral is 180.

Therefore, from the figure

$\angle B A D+\angle B C D=180^{\circ}$

$x+2 y=180^{\circ} \ldots \text { (i) }$

Also,

$\angle A D C+\angle C B A=180^{\circ}$

$(x+y)+(2 x-y)=180^{\circ}$

$3 x=180^{\circ}$

$x=60^{\circ}$

Substitute $x=60^{\circ}$ in equation (i) we get;

$2 y=180^{\circ}-60^{\circ}$

$y=120 / 2=60^{\circ}$

Hence, the value of $x=y=60^{\circ}$.

Example 2: If PS || RQ and PQRS are cyclic quadrilaterals, determine the value of $\angle PQR$.

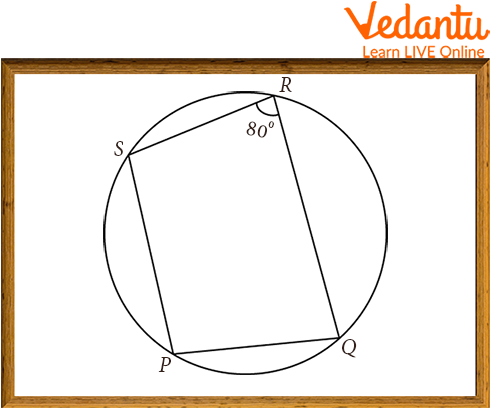
Cyclic Quadrilateral

Solution: PQRS is a cyclic quadrilateral, so the sum of either pair of opposite angles is 180 degrees.

$\angle P+\angle R=180^{\circ}$

$\angle P+80^{\circ}=100^{\circ}$

$\angle P=100^{\circ}$

Given PS || RQ. So, the Sum of interior angles is

$\angle \mathrm{SPQ}+\angle \mathrm{PQR}=180^{\circ}$

$\angle \mathrm{PQR}+100^{\circ}=180^{\circ}$

$\angle \mathrm{PQR}=80^{\circ}$

Hence, the value of $\angle P Q R$ is $80^{\circ}$.

Practice Questions

Q 1. PQRS is a cyclic quadrilateral. Diagonal PR and QS meet at A. If $\angle PAQ=110^{\circ}$ and$\angle RQS=30^{\circ}$ then $\angle PSQ$ measures

(a) $80^{\circ}$

(b) $70^{\circ}$

(c) $30^{\circ}$

(d) $50^{\circ}$

Ans: (a)

Q 2. In a cyclic quadrilateral ABCD, $\angle BCD= 120^{\circ}$ passes through the centre of the circle. Then the measure of $\angle ABD$ is

(a) $120^{\circ}$

(b) $30^{\circ}$

(c) $80^{\circ}$

(d) $50^{\circ}$

Ans: (b)

Summary

The four sides of a cyclic quadrilateral are the chords of the circle. An inscribed quadrilateral is another term for the cyclic quadrilateral. For a quadrilateral to be cyclic, its opposing angles must be supplementary to one another. The cyclic quadrilateral, its definition, theorems, properties, angles, and examples of cyclic quadrilateral problems with solutions are all covered in detail in this article. We hope this article will clear all our doubts regarding this topic.