An Introduction to Angle Sign
Do you know what an angle is? Do you know what an angle sign is? Let us study the angle and angle signs. When two lines join at a common point, an angle is formed. The lines need to meet at a common vertex and that vertex is called the vertex of the angle.
Some of the daily examples of angles can be seen in daily objects. Objects like chairs, scissors, pizza, fingers, etc. form angles signed by their shapes. The angle sign has two lines joined by a common vertex called the vertex point. Here, you will understand what is angle.
Properties of Angles
Important properties of the angle are:
For one side of a straight line, the sum of all the angles always measures 180 degrees.
The sum of all angles always measures 360 degrees around a point.
An angle is a figure where, from a common position, two rays appear. The vertex of the angle is called this point and its arms or sides are called the two rays forming the angle.
A reflex angle is called an angle which is greater than 180 degrees but less than 360 degrees.
They form a linear pair of angles if two opposite angles add up to 180 degrees.
The two opposite pairs of angles formed are called vertically opposed angles where two lines parallel each other.
Types of Angles
There are different kinds of angles based on their measurement. We will be studying acute angle, obtuse angle, right angle, reflex angle, straight angle, and complete angle.
Acute Angle: An Acute Angle is an angle whose angle measures less than 90 degrees. Such angles as 60 degrees, 50 degrees, etc. are acute angles.
Right Angle: A Right Angle is an angle that measures exactly 90 degrees. The angle at 90 degrees is always a right angle.
Obtuse Angle: Obtuse Angle is an angle whose angle measures between 90 degrees to 180 degrees. Angles at 120 degrees, 150 degrees, etc. are Obtuse Angles.
Straight Angle: A Straight Angle is an angle whose angle measures exactly 180 degrees. This is called a straight angle.
Reflex Angle: A Reflex Angle is an angle whose angle measures between 180 degrees to 360 degrees. Angles at 200 degrees, 260 degrees, etc. are Reflex Angles.
Complete Angle: A Complete Angle is an angle whose angle measures exactly 360 degrees. This is called a complete angle.
Types of Angles
Angle Based on the Rotation
Based on the direction of measurement or the direction of rotation, angles can be of two types:
Positive Angle
Negative Angle
A Positive Angle is an angle that forms from counter-clockwise rotation. The ray moves in a counterclockwise direction from its initial position to the final position.
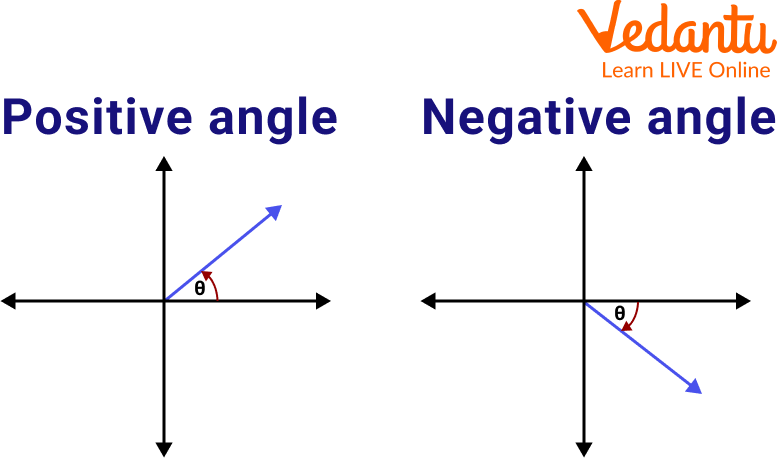
Positive & Negative Angle
A Negative Angle is an angle that forms from clockwise rotation. The ray moves in a clockwise direction from an initial position to the final position. Let us understand both concepts with the help of an example.
In the left side diagram, the ray is going counterclockwise from the initial side to the final position. In the right side diagram, the ray is going in a clockwise direction from the initial position to the final position. Hence, the left side diagram is the positive angle and the right side diagram is the negative angle.
Pair of Angles
By combining two angles, we can create different types of angles, such as:
Complementary angles: If the sum of the two angles is 180°, they are called complementary angles.
Supplementary angles: If the sum of the two angles is 90°, they are called supplementary angles.
Linear Pair: If the non-common arms of adjacent angles are exactly opposite each other or extend in the other direction, then they are called linear pairs. By linear, it is clear that they form a straight line.
Adjacent angles: If two angles are attached to a common arm and have a common vertex, so they are considered adjacent angles, and the non-common arms are on either side of the common arm, too.
Vertically Opposite Angles: The angle created on either side of the common vertex is called vertical angles or vertically opposite angles if both lines converge at a single point (called the vertex).
Fun facts
The term "angle" came from the Latin word Angulus, which means "a little bending."
Eudemus, who defined an angle as a deviation from a straight line, first used the concept of angle.
Summary
An angle is a formation of two lines meeting at a common endpoint called the vertex. These angles can either be positive or negative. A positive angle forms from the counterclockwise direction of the rays and a negative angle is formed from the clockwise direction of the rays. Acute Angle, Obtuse Angle, Right Angle, Reflex Angle, Complete Angle, and Straight Angle are the types of Angles. Vertex, Arms, Initial Side, and Reference Side are the parts of an Angle. Now, it is clear what the angle is.
FAQs on Angle Definition
1. What is Meant By Interior and Exterior Angles?
The angle formed on the inside of a circle is considered as the internal angle, while the exterior angle is the angle formed on the outside of the shape.
2. What are the Six Different Angles in Geometry Based on Measurement?
Six different angles based on magnitude are:
Acute angle, Obtuse angle, Right angle, Straight angle, Reflex angle, and full angle.
3. Where are angles used in real life?
Engineers and architects use angles for building, measurement, designing, etc. Architects and engineers use it to design roads, buildings, and sporting facilities.
