Right Angle

In geometry, an angle is formed when two rays are joined together at a common point. Here the common point is called the node or vertex and two rays are called arms of the angle. An angle is a form of geometrical shape, which is constructed by joining two rays to each other at their end-points. Majorly there are six types of angles in geometry. In this article, we will learn one of these angles i.e right angle definition, triangle and its properties.

An equilateral triangle has three congruent sides. The area of a triangle is determined by the base and the height. Using the Pythagorean Theorem, we can calculate the area accordingly.

One of the best-known mathematical formulas is the Pythagorean Theorem, which gives us an overview of the relationship between the sides of a right triangle. A right triangle consists of two legs and one hypotenuse. The two legs meet at a 90° angle, and the hypotenuse is the longest side of the right-angle triangle and it is the side opposite to the right angle. 

In a right-angled triangle, the algorithm of a right-angled triangle calculator uses the Pythagorean theorem to calculate the hypotenuse or one of the other two sides, as well as the Heron formula to find the area and the standard triangle perimeter formula. Moreover, it allows specifying angles either in grades or radians for a bit more flexibility. 

1. Right-angled triangles- In a right-angled triangle, the side which is opposite to the right side is called by its hypotenuse, and the remaining two sides by the base and altitude. 

2. Acute Angled Triangles - If all the three angles of a triangle are acute, i.e if they are less than 90 degrees, then the triangle is called acute-angled. 

3. Obtuse Angled Triangles- An obtuse triangle is a triangle that has one obtuse angle i.e. they have an angle that is greater than 90°.

Right Angle Definition

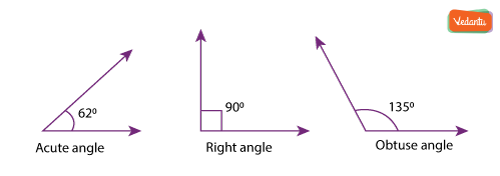
If the measure of the angle between two rays is exactly equal to 90 degrees, then the angle is called a right angle. Angles whose measure is less than 90° such as 87°, 56°, 77°, 42°, etc. are known as acute angles and the angles whose measure is more than 90° such as 91°, 98°, 102°, 150°, 167°, etc., are known as obtuse angles.

The measure of a right angle is written in terms of degrees i.e 90° and in terms of radians as\[ \frac{\pi}{2}\] (= 1.5708) radians.

The below figure shows the shape of the angle formed by two rays.

Right Angle Triangle

A right-angled triangle is a triangle having an angle between the base and the perpendicular 90°. It has three sides named, “base” “hypotenuse” and “perpendicular”. A right-angled triangle is one of the basic shapes in geometry and it is the foundation of trigonometry.

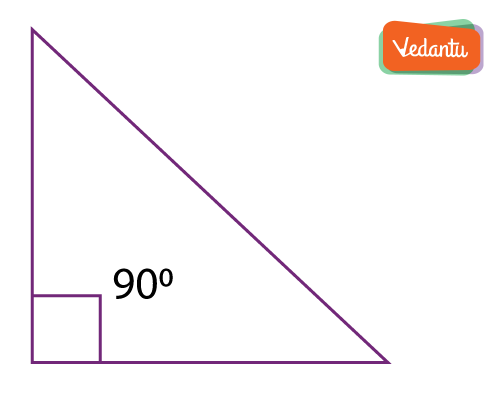
In the right triangle, the hypotenuse is the longest side and is opposite to the right angle of the triangle.

Right Angle Triangle Formula

The formula used to determine whether the given triangle is the right triangle or not is known as the Pythagoras theorem. The theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides.

\[(\text{Hypotenuse})^{2} = (\text{Adjacent side})^{2} + (\text{Opposite side})^{2}\]

Right Angle Triangle Properties

Following are some of the important properties of a right angle triangle: 

• In a right-angled triangle, the measure of one angle is exactly equal to 90 degrees.

• The angles other than the right angle must be acute angles, i.e. less than 90 degrees.

• The side opposite to vertex of 90 degrees is called the hypotenuse of the right triangle and it is the longest side of the triangle

• The other two sides which are adjacent to the right angle are called base and perpendicular.

• The circumcircle of the right angle triangle passes through all three vertices, and the radius of this circle is equal to half of the length of the hypotenuse.

• If one of the angles is 90° and the measure of the other two angles is 450 each, then the triangle is called an Isosceles Right Angled Triangle, where the adjacent sides to 90° are equal in length.

Area of a Right Triangle

The area of a right triangle is the area enclosed by three sides of the triangle in a plane. The formula to find the area of a right triangle is given below:

\[Area (A) = \frac{1}{2} * Base * Height\]

Here, Height = Perpendicular

Right Angle Isosceles Triangle

When two sides other than hypotenuse, i.e. base and perpendicular are congruent in a right triangle, then it is called a right angle isosceles triangle or simply isosceles right triangle. In a triangle, the angles made by the base and perpendicular with the hypotenuse are congruent, i.e. measure of both the angles is 45 degrees.

Right Angle Example

We can observe right angles shapes in many daily life objects such as edges of a book meeting at right angles at the vertices, sides of a rectangular table, and boards in classrooms forming right angles at the corners. The below figure shows the rectangular board that has right angles at its corners.

As we know all the interior angles of a square are right angles, i.e. equal to 90 degrees as shown in the below figure.

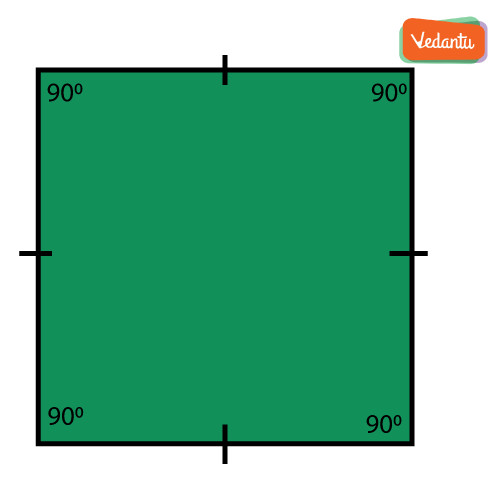
Also, the angle formed by the x-axis and y-axis in the coordinate plane at the center (intersection of axes) is the right angle.

 Facts

• All right angles correspond to a quarter of a complete turn.

• All triangles which have one angle right are called right-angled triangles.

• The formula of right-angle triangle is also known as Pythagoras Theorem

Solved Example:

Question: Find is the Value of the Hypotenuse of the Right-Angled Triangle if the Value of the Adjacent and Opposite Sides are 20 cm and 15 cm respectively.

Solution: Given

Adjacent side = 20 cm

Opposite side = 15 cm

According to the right angled triangle formula 

\[(\text{Hypotenuse})^{2} = (\text{Adjacent side})^{2} + (\text{Opposite side})^{2}\]

\[ = (20)^{2} + (15)^{2}\]

= 400 + 225

= 625 cm

\[ \Rightarrow   {\text{hypotenuse}} = \sqrt{625} cm = 25 cm\]

Hence, the hypotenuse is 25 cm.

Conclusion:

The most important formulas of trigonometry are those of a right-angled triangle. If θ is one of the acute angles in a triangle, then the sine of theta is always the ratio of the opposite side to the hypotenuse, the cosine is the ratio of the adjacent side to the hypotenuse. This article focuses on the Right angle and its application. You can solve the already solved examples again to understand them better. Trigonometry can be a little tricky but we have tried to make it easier for you all.