Question

Which of the following points lies on the locus of the foot of perpendicular drawn upon any tangent to the ellipse $\left( {\dfrac{{{x^2}}}{4}} \right) + \left( {\dfrac{{{y^2}}}{2}} \right) = 1$ from any of its foci?
A. $\left( { - 1,\sqrt 3 } \right)$
B.$\left( { - 2,\sqrt 3 } \right)$
C. $\left( { - 1,\sqrt 2 } \right)$
D. $\left( {1,2} \right)$

Answer 1

Hint: The standard form of the ellipse is represented as $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$. First, we will rearrange the given equation of an ellipse in the standard form. Also, the tangent to the ellipse in its standard form is given as $y = mx + \sqrt {{a^2}{m^2} + {b^2}} $ where $m$ is the slope of the tangent. Then, we will find the locus of the foot of the perpendicular drawn upon any tangent by taking a general point $(h,k)$.

Complete step by step Solution:
Firstly, we draw an ellipse with foci A and B and a tangent to the ellipse passing through point $C(h,k)$. Here, $C(h,k)$ is also the foot of the perpendicular from the focus $B$ of the ellipse to the tangent at $C$.

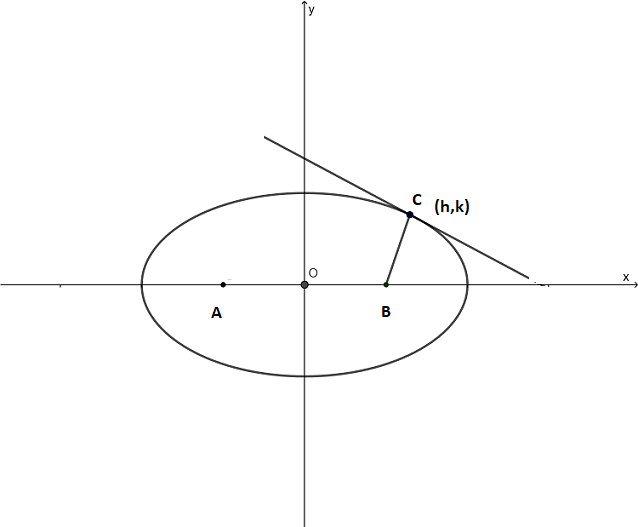
Comparing the given equation $\left( {\dfrac{{{x^2}}}{4}} \right) + \left( {\dfrac{{{y^2}}}{2}} \right) = 1$ with the standard equation of an ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ we get;
${a^2} = 4$ and ${b^2} = 2$
$ \Rightarrow a = 2$ and $b = \sqrt 2 $
(The positive values will give focus on the positive x-axis, similarly, negative values will give focus on the negative x-axis. We consider positive values here since in question it is asked from any one of the focus point.)
Eccentricity $e$of the ellipse is expressed as $e = \sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}} $. Here,
$e = \sqrt {1 - \dfrac{2}{4}} $
$e = \dfrac{1}{{\sqrt 2 }}$.
The focus of the ellipse is defined as $(ae,0)$. Here, the focus will be $B\left( {\sqrt 2 ,0} \right)$ (see diagram).
Now we know that equation of the tangent to the parabola is given as:
$y = mx + \sqrt {{a^2}{m^2} + {b^2}} $ …(1)

Substituting ${a^2} = 4$ and ${b^2} = 2$ in equation (1), we get ;
$y = mx + \sqrt {4{m^2} + 2} $ …(2)
The equation of a tangent to the ellipse at $C(h,k)$ is, from equation (2),
$k = mh + \sqrt {4{m^2} + 2} $ …(3)
Rearranging and squaring, we have,
${\left( {k - mh} \right)^2} = 4{m^2} + 2$ …(4)
Line perpendicular i.e. $BC$ to the tangent from focus B will have a slope $ - \dfrac{1}{m}$; since the product of slopes of two perpendicular lines is $ - 1$.
We can write the equation of line $BC$ having slope $ - \dfrac{1}{m}$as using point slope form i.e. $y - {y_1} = m\left( {x - {x_1}} \right)$. Here \[B\left( {{x_1},{y_1}} \right) = \left( {\sqrt 2 ,0} \right)\] and $slope(m) = - \dfrac{1}{m}$. The equation of line BC is
$y - 0 = - \dfrac{1}{m}\left( {x - \sqrt 2 } \right)$
Rearranging we get,
$ - my = x - \sqrt 2 $ …(5)
Since, point $C(h,k)$ also lies on line $BC$it will satisfy the equation (4). Putting $(h,k)$in equation (4) we get,
$ - mk = h - \sqrt 2 $ …(6)
Rearranging and squaring, we have,
${\left( {h + mk} \right)^2} = 2$ …(7)
Adding equations (4) and (7)
${\left( {k - mh} \right)^2} + {\left( {h + mk} \right)^2} = 4{m^2} + 2 + 2$
${k^2} + {m^2}{h^2} - 2mkh + {h^2} + {m^2}{k^2} + 2mkh = 4(1 + {m^2})$
Solving further and taking the common terms on both sides we have,
${h^2} + {k^2} = 4$ …(8)
This is the equation of the circle; hence the locus of general point $C(h,k)$ is a circle.
To get a general equation $h \to x;y \to k$ in equation (8).
${x^2} + {y^2} = 4$ …(8)
Now check the given options which satisfy the equation (8).
Take $\left( { - 1,\sqrt 3 } \right)$ and substitute in LHS of equation (8).
$
 {( - 1)^2} + {(\sqrt 3 )^2} \\
  = 4 \\
 $
$ = $RHS.
Therefore, $\left( { - 1,\sqrt 3 } \right)$lies on the locus of the foot of perpendicular drawn upon any tangent to the ellipse $\left( {\dfrac{{{x^2}}}{4}} \right) + \left( {\dfrac{{{y^2}}}{2}} \right) = 1$ from any of its foci.

Hence, the correct option is (A).

Note:We take a generic point $C(h,k)$ to represent all the tangents at all points that lie on the ellipse. In this question, we have taken all the positive values i.e. $a\& b$, and the focus point lying on the positive x-axis to ease the calculation.