
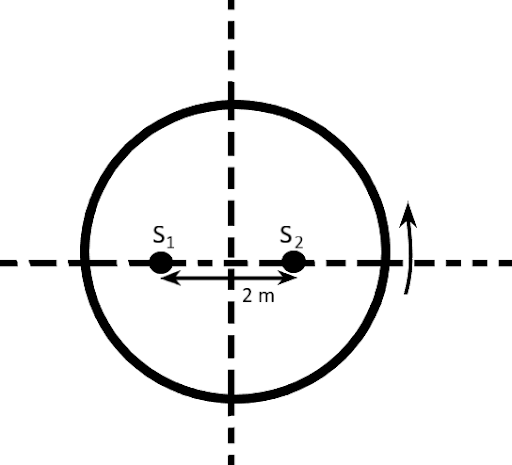
Two points sources separated by $2.0\,m$ are radiating in phase with $\lambda = 0.50\,m$. A detector moves in a circular path around the two sources in a plane containing them. How many maxima are detected?
A. $16$
B. $20$
C. $24$
D. $32$
Answer
216.3k+ views
Hint:When the two waves superimpose on each other to give a wave of greater amplitude, that is interference. A spot in an interference pattern where the interfering waves are maximally constructive. Interference maxima occurs at angles $\theta $such that $d\,\sin \theta = m\lambda $where $m$ is an integer. To determine the total number of maxima, you need to observe the given figure and then use the interference maxima.
Formula used:
Interference maxima occurs at angles \[\theta \] such that \[d\,\sin \theta = m\lambda \] where \[m\] is an integer.
Complete step by step solution:
In the question, two sources ${S_1}$and ${S_2}$ are given which are separated by $d = 2.0\,m$ and are radiating in phase with wavelength $\lambda = 0.50\,m$. As we know that the Interference maxima occur at angles $\theta $ such that,
$d\,\sin \theta = m\lambda $,
Here, the total number of maxima is $m$ which is an integer.
Apply the constructive interference for maxima and put the given information in the interference maxima, then:
$(2.0)\,\sin \theta = m(0.50) \\$
$\Rightarrow \sin \theta = \dfrac{{0.50}}{{2.0}}m \\$
$\Rightarrow \sin \theta = 0.25m $
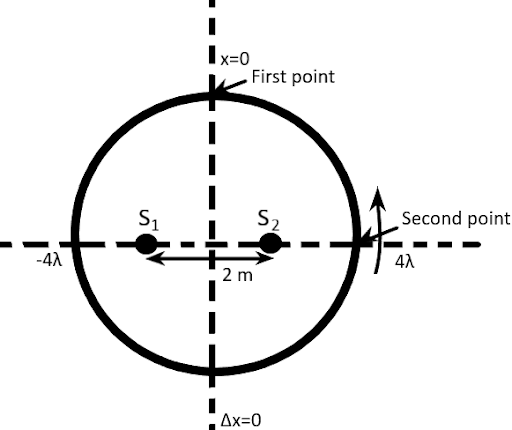
As $\sin \theta $ lies between $ - 1$ and $1$, so we need to find all values of $m$ for which $|0.25m| \leqslant 1$. Here $m$ is an integer, then: these values are $ - 4, - 3, - 2, - 1,0,1,2,3,4$. For each of these there are $2$ different values of $\theta $ except for $ - 4$ and $ + 4$, we get the single value of $\theta $. Thus at the second point there is a path difference of $4\lambda $ and at the first point there is a path difference of zero. So, between ${0^{th}}$ order and ${4^{th}}$ order will lie $1st,\,2nd,\,3rd$ maxima. This same procedure repeats in all other quadrants also. Therefore, a total of $16$ maxima points.
Thus, the correct option is A.
Note: At point second, the path difference is $2.0\,m$ and at the first point, the path difference is zero. While moving from first point to second point, the path difference changes from $2.0\,m$to zero, making two maxima exclude the second point. Second point is common for both upper quarter circles so there are $16$ angels at different angles in all.
Formula used:
Interference maxima occurs at angles \[\theta \] such that \[d\,\sin \theta = m\lambda \] where \[m\] is an integer.
Complete step by step solution:
In the question, two sources ${S_1}$and ${S_2}$ are given which are separated by $d = 2.0\,m$ and are radiating in phase with wavelength $\lambda = 0.50\,m$. As we know that the Interference maxima occur at angles $\theta $ such that,
$d\,\sin \theta = m\lambda $,
Here, the total number of maxima is $m$ which is an integer.
Apply the constructive interference for maxima and put the given information in the interference maxima, then:
$(2.0)\,\sin \theta = m(0.50) \\$
$\Rightarrow \sin \theta = \dfrac{{0.50}}{{2.0}}m \\$
$\Rightarrow \sin \theta = 0.25m $

As $\sin \theta $ lies between $ - 1$ and $1$, so we need to find all values of $m$ for which $|0.25m| \leqslant 1$. Here $m$ is an integer, then: these values are $ - 4, - 3, - 2, - 1,0,1,2,3,4$. For each of these there are $2$ different values of $\theta $ except for $ - 4$ and $ + 4$, we get the single value of $\theta $. Thus at the second point there is a path difference of $4\lambda $ and at the first point there is a path difference of zero. So, between ${0^{th}}$ order and ${4^{th}}$ order will lie $1st,\,2nd,\,3rd$ maxima. This same procedure repeats in all other quadrants also. Therefore, a total of $16$ maxima points.
Thus, the correct option is A.
Note: At point second, the path difference is $2.0\,m$ and at the first point, the path difference is zero. While moving from first point to second point, the path difference changes from $2.0\,m$to zero, making two maxima exclude the second point. Second point is common for both upper quarter circles so there are $16$ angels at different angles in all.
Recently Updated Pages
Wheatstone Bridge Explained: Working, Formula & Uses

Young’s Double Slit Experiment Derivation Explained

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Electricity and Magnetism Explained: Key Concepts & Applications

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Understanding Atomic Structure for Beginners

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Electromagnetic Waves and Their Importance

Understanding the Electric Field of a Uniformly Charged Ring




