Question

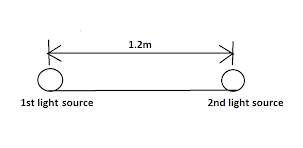
Two light sources with equal luminous intensity are lying at a distance of 1.2 m from each other. Where should a screen be placed between them such that illuminance on one of its faces is four times that on another face?
A. \[0.2{\text{ }}m\]
B. \[0.4{\text{ }}m\]
C. \[0.8{\text{ }}m\]
D. \[1.6{\text{ }}m\]

Answer 1

Hint: First think how light propagates through any surface. Then find out the relation between intensity of light with distance. Now you can draw the picture to make the question easier. At last, assume a distance x m form source and solve the equations.

Formula used:
The expression of intensity of wave is,
$I = \dfrac{{{\text{amount of light }}}}{{{\text{area }}}}$
\[{E_2} = 4{E_1}.{\text{ }}If{\text{ }}x{\text{ is distance from 1st source}},\]
Here ${E_1} = {\text{ intensity of light of 1st source}}$ and ${E_2} = {\text{ intensity of light of 2nd source}}$

Complete step by step solution:
First make a diagram for proper visualization

light intensity and distance are inversely proportional with each other. as the distance increases, the light intensity decreases. if the light source moves farther away, the light spreads over to more area. So light decreases in specific proportion with distance of light. Up to this all we say is general observation. Now let’s check this out scientifically. how light propagates through a medium. Let’s see it with a picture.


So now we can easily observe how light is really propagated. But it is a 2D view in 3D it obviously looks like a sphere. Now come to the point : what is the intensity of light? Intensity of light means the amount of light (lumens) falling on a surface over any given $foo{t^2}$or ${m^2}$. That says light intensity can be written in terms of lumens per square foot (foot candles) or lumens per square meter (lux).

If we formulize it then we get
$I = \dfrac{{{\text{amount of light }}}}{{{\text{area }}}}$
$\Rightarrow I= \dfrac{{{\text{amount of light}}}}{{4\pi {r^2}}}$
$\Rightarrow I= \dfrac{{{\text{amount of light}}}}{{\dfrac{4}{3} \times \pi {r^2}}}$
In both the cases we can clearly see that light is proportional to the inverse of ${r^2}$ which means the square of distance. I think Up to now it's all clear. So, we can say that $I\varpropto\dfrac{1}{{{r^2}}}$.

In the given question we have to find a place between them such that the illuminance on one of its faces is four times that on another face. Let’s solve it. Let’s take the required distance at a $x{\text{ m}}$ from the first object. So, now we can compare at this point due to two sources.
\[{E_2} = 4{E_1}.{\text{ }}If{\text{ }}x{\text{ is distance from 1st source}},\]
Here ${E_1} = {\text{ intensity of light of 1st source}}$ and ${E_2} = {\text{ intensity of light of 2nd source}}$.
\[\dfrac{I}{{{{(1.2 - x)}^2}}} = \dfrac{I}{{4{x^2}}}\]
\[\Rightarrow \dfrac{1}{{1.2 - x}} = \dfrac{2}{x}\]
\[\Rightarrow 3x = 2.4\]
\[\therefore x = 0.8\,m\]
Hence our answer is $0.8\,m$.

Therefore, option C is the correct answer.

Note: As the distance increases, the light intensity decreases. If the light source moves farther away, the light spreads over to more areas. Light is proportional to the inverse of ${r^2}$ which means the square of distance.