Question

Two equal parabolas have the same focus and their axes are at right angles. A normal to one is perpendicular to normal to the other. Prove that the locus of the point of intersection of these normals is another parabola

Answer 1

Hint: Equation of normal to parabola \[{{y}^{2}}=4ax\] is given as \[y=mx-2am-a{{m}^{3}}\], where \[m\] is the slope of the normal.

We will consider the equation of one of the parabolas as \[{{y}^{2}}=4ax\].


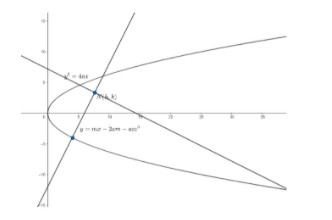
So , its focus is \[S\left( a,0 \right)\].
We know, the equation of normal to the parabola in slope form is given as
\[y=mx-2am-a{{m}^{3}}....\left( i \right)\] , where \[m\] is the slope of the normal.
Now , we have to find the locus of intersection of the normal.
We will consider this point to be \[N\left( h,k \right)\].
Now, since \[N\left( h,k \right)\] is the point of intersection of the normals , so , it should lie on equation \[\left( i \right)\], i.e. the point \[N\left( h,k \right)\] should satisfy equation \[\left( i \right)\].
So , we will substitute \[x=h\] and \[y=k\] in equation \[\left( i \right)\].
On substituting \[x=h\] and \[y=k\] in equation \[\left( i \right)\] , we get
 \[k=mh-2am-a{{m}^{3}}\]
Or , \[a{{m}^{3}}+m\left( 2a-h \right)+k=0....\left( ii \right)\]
Clearly, we can see that equation \[\left( ii \right)\] is a cubic equation in \[m\] , which is of the form \[a{{m}^{3}}+b{{m}^{2}}+cm+d=0\]. So , it should represent three lines passing through \[\left( h,k \right)\].
Now, in the question , it is given that two perpendicular normals pass through \[N\left( h,k \right)\]. So , out of these three lines , two lines must be perpendicular.
Now , let \[{{m}_{1}},{{m}_{2}}\] and \[{{m}_{3}}\] be three roots of equation \[\left( ii \right)\]. The roots of the equation \[\left( ii \right)\] are corresponding to the slopes of the three lines.
Now, we are given two of these lines are perpendicular.
We know , when two lines are perpendicular , the product of their slopes is equal to \[-1\] .
So, \[{{m}_{1}}{{m}_{2}}=-1....\left( iii \right)\]
We know , for a cubic equation of the form \[a{{m}^{3}}+b{{m}^{2}}+cm+d=0\], the product of the roots is given as \[\dfrac{-d}{a}\].
So , from equation \[\left( ii \right)\] , we have
\[{{m}_{1}}{{m}_{2}}{{m}_{3}}=\dfrac{-k}{a}\]
Since , \[{{m}_{1}}{{m}_{2}}=-1\text{ }\left( \text{from equation }iii \right)\]
So, \[{{m}_{3}}=\dfrac{k}{a}\]
Now , \[{{m}_{3}}\] is a root of equation \[\left( ii \right)\]. So , it should satisfy the equation.
So , \[a{{\left( \dfrac{k}{a} \right)}^{3}}+\dfrac{k}{a}\left( 2a-h \right)+k=0\]
Or \[\dfrac{{{k}^{3}}}{{{a}^{2}}}+2k-\dfrac{kh}{a}+k=0\]
Or \[{{k}^{2}}+3{{a}^{2}}-ah=0\]
Or \[{{k}^{2}}=a\left( h-3a \right)\]
Now , the locus of \[N\left( h,k \right)\] is given by replacing \[\left( h,k \right)\] by \[\left( x,y \right)\]
So, the locus of \[N\left( h,k \right)\] is given as \[{{y}^{2}}=a\left( x-3a \right)\] which is the equation of a parabola.

Note: The product of slopes of perpendicular lines is equal to \[-1\] and not \[1\]. Students generally get confused and make this mistake.