Question

Two boys of masses \[10kg\] and \[8kg\] are moving along a vertical light rope, the former climbing up with an acceleration of \[2m/{s^2}\] when the latter coming down with a uniform velocity of \[2m/s\]. Find tension in the rope at the fixed support will be: \[\left( {g = 10m/{s^2}} \right)\]
A) \[200N\]
B) \[120N\]
C) \[180N\]
D) \[160N\]

Answer 1

Hint: First we calculate tension due to boy A. Then we calculate tension due to B. After that total tension is calculated as the sum of two tensions. Tension is given by production of mass and acceleration of gravity or gravitational acceleration.

Formula used:
We use a free body diagram method to calculate tension in rope. Tension in rope due to boy A and boy B is calculated by \[T = mg\].

Complete step by step solution:
Given: mass of boy A, \[{m_A} = 10kg\] and mass of boy B, \[{m_B} = 8kg\], \[g = 10m/{s^2}\], velocity of boy having mass in upward direction is \[{v_A} = 2m/s\] and boy A climbing up with an acceleration \[a = 2m/{s^2}\].
Suppose the tension = T

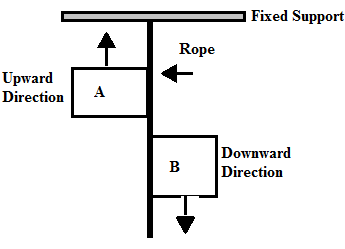
From free body diagram
Tension due to Boy on A moving in upward direction,
\[{T_A} = {m_A}(g + a)\]
\[
   \Rightarrow {T_A} = 10\left( {10 + 2} \right)N \\
  \therefore {T_A} = 120N \\
 \]
Tension due to boy B moving in downward direction,
\[
  {T_B} = {m_B}g \\
   \Rightarrow {T_B} = 8 \times 10N \\
  \therefore {T_B} = 80N \\
 \]
Total tension occurs in rope due to both boys A and B
\[T = {T_A} + {T_B}\]
\[
\Rightarrow T = 120N + 80N \\
  \therefore T = 200N \\
 \]
Total tension in rope, \[T = 200N\].

Hence, option A is the correct answer.

Additional information: A Free-Body Diagram is used to represent all forces and moments acts on an object. The purpose of this diagram is to simplify a given problem. Students may use this diagram to simplify complicated calculations to find unknown variables. Unknown variables may be one of the force directions, force magnitudes, or moments. Tension force is described by the pulling force applied on an object by a rope, chain, cable.

Note: Students must be careful to draw free body diagrams (FBD). Students must be careful about directions of boy A and B. For boy A direction is upward and for boy B direction is downward. So total tension in a rope is calculated by the sum of both tensions occurring due to both boys.