Question

Two balls of same mass and carrying equal charge from a fixed support of length l electrostatic equilibrium, assuming that angles made by each thread is small, the separation between the balls is proportional to
A. $l$
B. ${l^2}$
C. ${l^{\dfrac{2}{3}}}$
D. ${l^{\dfrac{1}{3}}}$

Answer 1

Hint: Think about the condition of equilibrium. Think about electrostatic force, gravitational force and how they are acting on the balls. Apply the equilibrium condition and try to find relation between length of string and separation between them.

Complete step by step solution:
First to understand the situation clearly let’s draw the picture

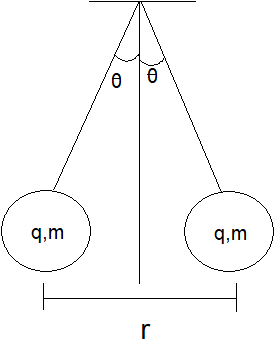
According to the question, let's assume we have two balls of the same mass and charge of $q{\text{ and m}}$ respectively and the distance between them is $r$ . The whole system is in electrostatic equilibrium. A system is in equilibrium means net force on the body is zero and net torque of the body is zero. That means here the net electrostatic force of the system is zero.

Lets see what are the forces acting on the system. We can see that between charges there is always an electrostatic force. We can calculate this electrostatic force by applying coulomb's law which says that $F = k \times \dfrac{{{q_1} \times {q_2}}}{{{r^2}}}$here $F = {\text{force}}$ , ${q_1},{q_2} = {\text{charges}}$ , $r = {\text{distance between their centres}}$. Another force is gravitational force which is equal to the product of mass of the body with gravitational acceleration. Another force is shown in the figure is tension on the string. Let’s assume it as $T$ . Let’s see the free body diagram of the ball.


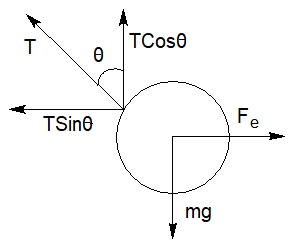
Observe the free body diagram carefully, for making the whole system equilibrium we have to make the sum of all forces zero. Let’s start with the horizontal direction, there are two forces. We can that from $\vec T\sin \theta + {\vec F_e} = 0$, here ${\vec F_e} = {\text{ electrostatic force}}$, $T = {\text{ tension on the string}}$.

Now its is clear to us is \[\left| {\vec T\sin \theta } \right| = \left| {\overrightarrow {{F_e}} } \right|\]. Now consider that the length of the string is $l$. Let’s find out the value of $\sin \theta $. For this first draw a triangle.

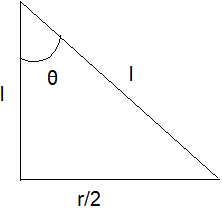
Now in this triangle $\sin \theta $ is equal to $r/2l$. Where$r = {\text{ distance between balls, l = length of string}}$ . Now put the value of $\sin \theta $ in the equation. We get $T \times \left( {\dfrac{r}{{2l}}} \right) = {F_e}$. Now the value of ${F_e} = k \times \dfrac{{{q^2}}}{{{r^2}}}$ by applying coulomb's law.
Hence,
$T = k \times \dfrac{{{q^2}}}{{{r^2}}} \times \left( {\dfrac{{2l}}{r}} \right) = k\dfrac{{\left( {{q^2} \times 2l} \right)}}{{{r^3}}}\\$
Next we have made the sum of force in the vertical direction zero. $T\cos \theta = mg$ because they are opposite directions so for making net force zero the magnitude of two forces must be the same.

From the triangle we can say that $\cos \theta = 1$ because in the question it is mentioned $\theta $ is very small. If we can say that \[T = mg\] . Then, we can compare values of $T$ getting from two equations. Let’s compare them. $k\dfrac{{\left( {{q^2} \times 2l} \right)}}{{{r^3}}} = mg$. From this equation we can say that $l$ is proportional to ${r^3}$. We can rewrite it as $r$ is proportional to ${l^{\dfrac{1}{3}}}$.

Hence, Option D is the correct answer.

Note: Equilibrium condition is that when net force and net torque the system is zero. In that type of first try to visualise the situation. Making a free body diagram makes this kind of problem easier. always breaks the force like the tension into two parts .