Question

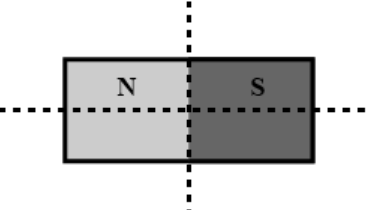
Time period for a magnet is T. If it is divided in four equal parts along its axis and perpendicular to its axis as shown then time period for each part will be

A. $4T$
B. $\dfrac{T}{4} \\ $
C. $\dfrac{T}{2} \\ $
D. $T$

Answer 1

Hint: The length bar magnet must be divided into four equal parts, each of which must have the same length and width. The bar magnet can only be divided into four equal parts by first cutting it parallel to its length and then perpendicular to it, so that each piece is half as long as it originally was and half as wide.

Formula used:
The expression of time period of a magnet is,
$T = 2\pi \sqrt {\dfrac{I}{{MB}}} $
Here, $M$ is the magnetic moment, $B$ is the magnetic field and $I$ is the moment of inertia.

Complete step by step solution:
The term "bar magnet" refers to a magnetic bar. The poles are the ends of the bar magnet. A dipole is the bar magnet. Pole strength is the name of the physical property that describes the magnetization of the poles.

The magnet has been divided into four equal pieces by cutting it equally along its length and width, as shown in the diagram. To accomplish this, one must cut the magnets parallel to their length such that the length stays the same and the breadth is cut in half. The length must now also be cut in half because the magnet must once more be cut perpendicular to the length. The four pieces will therefore be equal. Time period of original magnet is given by
$T = 2\pi \sqrt {\dfrac{I}{{MB}}} $
Where $I$ is the inertia which is equal to $\dfrac{{m{L^2}}}{{12}}$ and $M = qL$

Since it is cut into 4 pieces the inertia will change. The new inertia is
${I^1} = \dfrac{{\dfrac{m}{4}{{(\dfrac{L}{2})}^2}}}{{12}} \\
\Rightarrow {I^1} = \dfrac{{m{L^2}}}{{16 \times 12}} \\
\Rightarrow {I^1} = \dfrac{I}{{16}}$
New dipole will be $ = \dfrac{q}{2} \times \dfrac{L}{2} = \dfrac{M}{4}$
So we can say that new time period
${T^1} = 2\pi \sqrt {\dfrac{{\dfrac{I}{{16}}}}{{\dfrac{{MB}}{4}}}} \\$
$\Rightarrow {T^1} = \dfrac{1}{2} \times 2\pi \sqrt {\dfrac{I}{{MB}}} \\ $
$\therefore {T^1} = \dfrac{T}{2}$

Hence option C is correct.

Note: The pole strengths alter depending on the length and area of the magnet after it has been cut, but the north and south poles stay the same. Each slice of the magnet is four times weaker than the original magnet due to reductions in the magnetization and magnetic moments.