Question

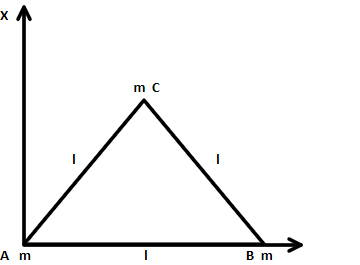
Three particles each of mass m gram, are situated at the vertices of an equilateral triangle ABC of the side \[1cm\]. The moment of inertia of the system (as shown in figure) about a line AX perpendicular to AB and in the plane of ABC in\[gram - c{m^2}\] units will be:
             

(A) $\dfrac{{3m{l^2}}}{4}$
(B) $2m{l^2}$
(C) $\dfrac{{5m{l^2}}}{4}$
(D) $\dfrac{{3m{l^2}}}{2}$

Answer 1

Hint: It is given that three masses of equal m grams, the distance of the point A, B and C can be calculated from AX by observing the diagram and then using the moment of inertia equation we can find the asked value.

Formula Used
\[I = M{a^2}\]

Complete step by step answer
We know that moment of inertia \[I = M{a^2}\], where M is the mass and a is the perpendicular distance from the rotation axis.
From the diagram, for each point let us first we will calculate the perpendicular distance
For point A, the perpendicular distance from AX axis$ = 0$
For point B, the perpendicular distance from AX axis$ = l$
For point C,
$\angle CAX = {30^0}$, since the interior angle of an equilateral triangle is ${60^0}$
Therefore, the perpendicular distance from AX axis$ = l\sin {30^0} = \dfrac{l}{2}$
Substituting the value of mass and perpendicular distance of each particle from axis in the equation we get,
The moment of inertia of the system will be the sum of moment of inertia at all point
\[I = {I_A} + {I_B} + {I_C} = 0 + m{l^2} + m{\left( {\dfrac{l}{2}} \right)^2} = m{l^2} + {\dfrac{{ml}}{4}^2}\]
$ \Rightarrow I = \dfrac{{5m{l^2}}}{4}$

Hence, the correct option is C.

Additional information
Moment of inertia corresponds to how mass acts in translational motion. We can say in other words mass can be seen as a measure of inertia. In rotational motion a force torque acts on the body which can be defined as the product of moment of inertia and angular acceleration of the body.

Note: Moment of inertia is nothing but the property by which a body opposes changes while rotating about an axis. The factors on which moment of inertia depends are the mass of the body, the shape and size and also mass distribution manner of the given body and the axis of rotation position.