
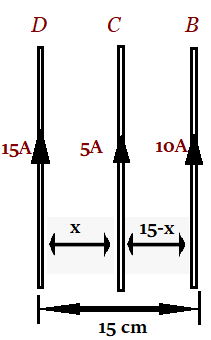
Three long, straight and parallel wires carrying currents are arranged as shown in the figure. The wire C carries a current of 5 and is so placed that it experiences no force. The distance of wire C from wire D is the
A. 9 cm
B. 7 cm
C. 5 cm
D. 3 cm
Answer
233.1k+ views
Hint:In order to answer this question, we will use the relationship between the force felt by conducting wires and the direction of parallel current flow. Further, we balance the force experienced by the middle conductor i.e., C; this will give us the required result. Also, we learn about some basic concepts of force and current.
Formula Used:
$F = \dfrac{{{\mu _0}{I_1}{I_2}}}{{2\pi r}}$
Complete answer:
The force experienced by C due to D will be inwards in direction and Similarly force on C by wire B will be outwards. Hence in equilibrium conditions these two forces will be equal and opposite. The surrounding medium, the current flowing through it, the current of the wire on which it acts, and the distance between them all affect the force produced by the magnetic field of a current carrying wire.
The force generated by a wire carrying current is:
$F = \dfrac{{{\mu _0}{I_1}{I_2}}}{{2\pi r}}$
Here, ${I_1}$ is the current flowing through one wire
${I_2}$is current flowing through another wire
$r$ is the separation of the two wires
For net force on wire C to be zero we balance the net force on C equal to zero,
Therefore, Force on wire C due to wire D= Force on wire C due to wire B
Let’s assume the distance of wire C from wire D is x.
Force on wire C due to wire D$ = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2 \times 15 \times 5}}{x}$
Force on wire C due to wire B$ = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2 \times 10 \times 5}}{{15 - x}}$
$ \Rightarrow \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2 \times 10 \times 5}}{{15 - x}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2 \times 15 \times 5}}{x}$
$x = 9cm$
Thus, the correct option is A.
Note: We should be aware that current-carrying conductors in parallel are subject to a constant force. Additionally, if the currents running through parallel wires are going in different directions, the wires will repel one another; yet, if the currents are going in the same direction, the wires will attract one another.
Formula Used:
$F = \dfrac{{{\mu _0}{I_1}{I_2}}}{{2\pi r}}$
Complete answer:
The force experienced by C due to D will be inwards in direction and Similarly force on C by wire B will be outwards. Hence in equilibrium conditions these two forces will be equal and opposite. The surrounding medium, the current flowing through it, the current of the wire on which it acts, and the distance between them all affect the force produced by the magnetic field of a current carrying wire.

The force generated by a wire carrying current is:
$F = \dfrac{{{\mu _0}{I_1}{I_2}}}{{2\pi r}}$
Here, ${I_1}$ is the current flowing through one wire
${I_2}$is current flowing through another wire
$r$ is the separation of the two wires
For net force on wire C to be zero we balance the net force on C equal to zero,
Therefore, Force on wire C due to wire D= Force on wire C due to wire B
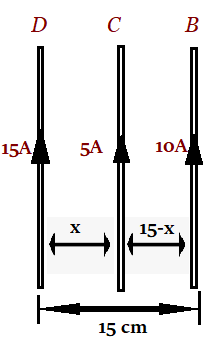
Let’s assume the distance of wire C from wire D is x.
Force on wire C due to wire D$ = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2 \times 15 \times 5}}{x}$
Force on wire C due to wire B$ = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2 \times 10 \times 5}}{{15 - x}}$
$ \Rightarrow \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2 \times 10 \times 5}}{{15 - x}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2 \times 15 \times 5}}{x}$
$x = 9cm$
Thus, the correct option is A.
Note: We should be aware that current-carrying conductors in parallel are subject to a constant force. Additionally, if the currents running through parallel wires are going in different directions, the wires will repel one another; yet, if the currents are going in the same direction, the wires will attract one another.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Uniform Acceleration in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Dual Nature of Radiation and Matter Class 12 Physics Chapter 11 CBSE Notes - 2025-26

Understanding the Electric Field of a Uniformly Charged Ring

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Derivation of Equation of Trajectory Explained for Students

Understanding Electromagnetic Waves and Their Importance




