Question

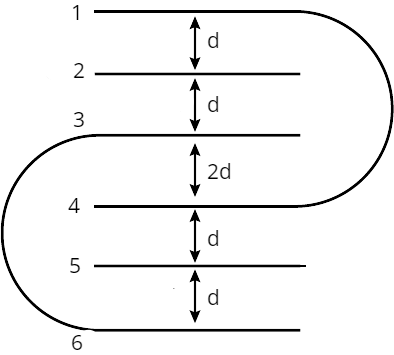
There are six plates of equal are $A$ and separation between the plates is $\mathrm{d}(\mathrm{d} \ll \mathrm{A})$ are arranged as shown in figure. The equivalent capacitance between points 2 and 5 , is $\alpha \dfrac{\varepsilon_{0} \mathrm{~A}}{\mathrm{~d}}$. Then find the value of $\alpha$.

Answer 1

Hint: An electrical device with two terminals known as a capacitor has the capacity to store energy in the form of an electric charge. It is made up of two electrical wires that are spaced apart by a certain amount. Vacuum may be used to fill the space between the conductors, or a dielectric, an insulating substance, may be used instead. Capacitance is the term used to describe a capacitor's capacity to hold charges.

Formula used:
The expression of capacitance is,
$C=\dfrac{{{\varepsilon }_{0}}A}{d}$
Here, A is the area of the cross section of the plate and d is the distance between the plates.

Complete step by step solution:
Rearrange the given plates as shown below

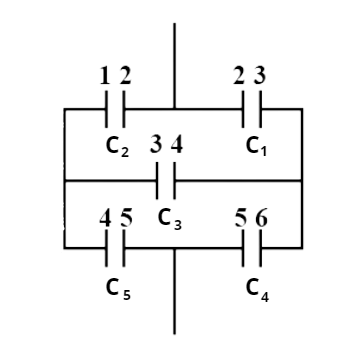
From this we get
${{C}_{1}}=\dfrac{{{\varepsilon }_{0}}A}{d},$
$\Rightarrow {{C}_{2}}=\dfrac{{{\varepsilon }_{0}}A}{2d}$
$\Rightarrow {{C}_{3}}=\dfrac{{{\varepsilon }_{0}}A}{3d},$
$\Rightarrow {{C}_{4}}=\dfrac{{{\varepsilon }_{0}}A}{2d},$
$\Rightarrow {{C}_{5}}=\dfrac{{{\varepsilon }_{0}}A}{d}$
$C_{1}$ and $C_{2}$ are in series and its effective capacity is
$\dfrac{\dfrac{\varepsilon_{0} A}{d} \times \dfrac{\varepsilon_{0} A}{2 d}}{\dfrac{\varepsilon_{0} A}{d}+\dfrac{\varepsilon_{0} A}{2 d}}=\dfrac{\varepsilon_{0} A}{3 d}$
The ratio of a system's electric charge change to the equivalent change in its electric potential is known as capacitance.
The effective capacitance of $C_{4}$ and $C_{3}=\dfrac{\varepsilon_{0} A}{3 d}$ is,
${{C}_{AB}}=\dfrac{{{\varepsilon }_{0}}A}{3d}+\dfrac{{{\varepsilon }_{0}}A}{3d}+\dfrac{{{\varepsilon }_{0}}A}{3d}$
$\Rightarrow C_{A B}=\dfrac{\varepsilon_{0} A}{3 d}+\dfrac{\varepsilon_{0} A}{3d}+\dfrac{\varepsilon_{0} A}{3 d}$
$\Rightarrow C_{A B}=\dfrac{\varepsilon_{0} A}{d}$
Substituting values we get
So the value of $\alpha =1$

Hence, the value of $\alpha$ is 1.

Note: The reciprocal of the equivalent capacitance when numerous capacitors are linked in series is equal to the total of the reciprocals of the individual capacitances. The equivalent capacitance is the total of the individual capacitances when many capacitors are connected in a parallel configuration. When numerous capacitors are linked in parallel, the equivalent capacitance is the sum of the individual capacitances. When a network of capacitors comprises a combination of series and parallel connections, we identify the series and parallel networks and compute their equal capacitances stepwise until the entire infrastructure is limited to a single equivalent capacitance.