
The vectors \[\bar A\vec B = 3\hat i + 5j + 4\hat k\] and \[\bar A\vec C = 5\hat i - 5j + 2\hat k\] are the sides of a triangle ABC. The length of the median through \[A\] is
A. \[3\]
B. \[ - 4\]
C. \[1\]
D. \[5\]
Answer
220.5k+ views
Hint: In the given question, we need to find the value of the length of the median through \[A\]. For this, we will find the position vector of \[AD\] and its modulus to get the desired result. Also, we will draw the diagram for this.
Formula used: The following formula used for solving the given question.
The modulus of a vector \[\vec u = a\hat i + b\hat j + c\hat k\] is given by
\[\left| {\vec u} \right| = \sqrt {{a^2} + {b^2} + {c^2}} \]
Complete step by step solution: Consider the following figure.
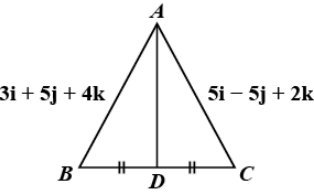
We know that the vectors \[\bar A\vec B = 3\hat i + 5j + 4\hat k\] and \[\bar A\vec C = 5\hat i - 5j + 2\hat k\] are the sides of a triangle ABC.
Here, we will find the position vector of \[AD\]
Thus, the position vector is given by
\[AD = \dfrac{{\left( {3 + 5} \right)\hat i + \left( {5 - 5} \right)\hat j + \left( {4 + 2} \right)\hat k}}{2}\]
By simplifying, we get
\[AD = \dfrac{{\left( 8 \right)\hat i + \left( 0 \right)\hat j + \left( 6 \right)\hat k}}{2}\]
By simplifying, we get
\[AD = \left( 4 \right)\hat i + \left( 3 \right)\hat k\]
Now, the length of a medium is given by
\[\left| {AD} \right| = \sqrt {{{\left( 4 \right)}^2} + {{\left( 3 \right)}^2}} \]
\[\left| {AD} \right| = \sqrt {16 + 9} \]
\[\left| {AD} \right| = \sqrt {25} \]
By taking square root, we get
\[\left| {AD} \right| = 5\]
Hence, the length of the median through \[A\] is \[5\] if the vectors \[\bar A\vec B = 3\hat i + 5j + 4\hat k\] and \[\bar A\vec C = 5\hat i - 5j + 2\hat k\] are the sides of a triangle ABC.
Thus, Option (D) is correct.
Additional Information:The definition of a vector is an entity with both magnitude and direction. The movement of an object between two points is described by a vector. The directed line segment can be used to geometrically represent vector mathematics. The magnitude of a vector is the length of the directed line segment, and the vector's direction is indicated by the angle at which it is inclined. A vector's "Tail" (the point where it begins) and "Head" (the point where it ends and has an arrow) are its respective names.
Note: Many students make mistake in finding the position vector of \[AD\]. This is the only way, through which we can solve the example in simplest way. Also, it is necessary to draw the figure to analyse the question to get the desired result.
Formula used: The following formula used for solving the given question.
The modulus of a vector \[\vec u = a\hat i + b\hat j + c\hat k\] is given by
\[\left| {\vec u} \right| = \sqrt {{a^2} + {b^2} + {c^2}} \]
Complete step by step solution: Consider the following figure.

We know that the vectors \[\bar A\vec B = 3\hat i + 5j + 4\hat k\] and \[\bar A\vec C = 5\hat i - 5j + 2\hat k\] are the sides of a triangle ABC.
Here, we will find the position vector of \[AD\]
Thus, the position vector is given by
\[AD = \dfrac{{\left( {3 + 5} \right)\hat i + \left( {5 - 5} \right)\hat j + \left( {4 + 2} \right)\hat k}}{2}\]
By simplifying, we get
\[AD = \dfrac{{\left( 8 \right)\hat i + \left( 0 \right)\hat j + \left( 6 \right)\hat k}}{2}\]
By simplifying, we get
\[AD = \left( 4 \right)\hat i + \left( 3 \right)\hat k\]
Now, the length of a medium is given by
\[\left| {AD} \right| = \sqrt {{{\left( 4 \right)}^2} + {{\left( 3 \right)}^2}} \]
\[\left| {AD} \right| = \sqrt {16 + 9} \]
\[\left| {AD} \right| = \sqrt {25} \]
By taking square root, we get
\[\left| {AD} \right| = 5\]
Hence, the length of the median through \[A\] is \[5\] if the vectors \[\bar A\vec B = 3\hat i + 5j + 4\hat k\] and \[\bar A\vec C = 5\hat i - 5j + 2\hat k\] are the sides of a triangle ABC.
Thus, Option (D) is correct.
Additional Information:The definition of a vector is an entity with both magnitude and direction. The movement of an object between two points is described by a vector. The directed line segment can be used to geometrically represent vector mathematics. The magnitude of a vector is the length of the directed line segment, and the vector's direction is indicated by the angle at which it is inclined. A vector's "Tail" (the point where it begins) and "Head" (the point where it ends and has an arrow) are its respective names.
Note: Many students make mistake in finding the position vector of \[AD\]. This is the only way, through which we can solve the example in simplest way. Also, it is necessary to draw the figure to analyse the question to get the desired result.
Recently Updated Pages
In a game two players A and B take turns in throwing class 12 maths JEE_Main

The number of ways in which 6 men and 5 women can dine class 12 maths JEE_Main

The area of an expanding rectangle is increasing at class 12 maths JEE_Main

If y xxx cdots infty then find dfracdydx A yxy 1 B class 12 maths JEE_Main

Mutually Exclusive vs Independent Events: Key Differences Explained

Area vs Volume: Key Differences Explained for Students

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

How to Convert a Galvanometer into an Ammeter or Voltmeter

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Understanding the Electric Field of a Uniformly Charged Ring

Understanding Electromagnetic Waves and Their Importance

Understanding Collisions: Types and Examples for Students

Understanding Atomic Structure for Beginners




