Question

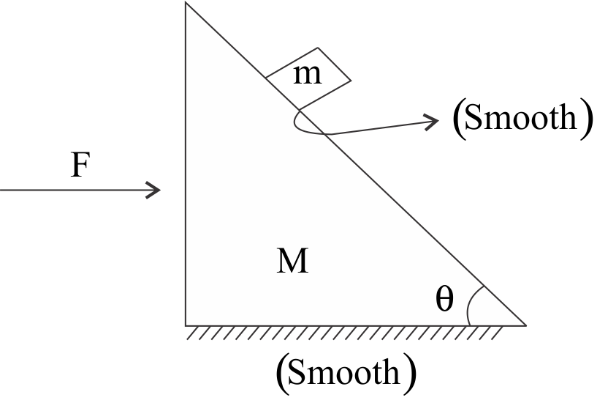
What will be the value of F for which the given block of mass $m$ remains stationary with respect to the wedge?

(A) $F = \dfrac{{\left( {M + m} \right)}}{{\operatorname{Tan} \theta }} \times g$
(B) $F = \left( {m + M} \right)g\operatorname{Tan} \theta $
(C) $F = \dfrac{{\operatorname{Tan} \theta }}{{\left( {M + m} \right)g}}$
(D) None of these

Answer 1

Hint: The block moves with acceleration with respect to ground. If a force F is applied to the system as shown in figure such that stationary with respect to block of mass M, then the magnitude of the body could be measured.

Complete step by step solution:
Acceleration is where force is and so this becomes a non inertial frame and the concept of pseudo force is used (ma) (refer to diagram) whose direction is always opposite to the acceleration.
Total mass here will be $M + m$
Force we know, $Force = mass \times acceleration$
Force in the case of inclination has two components in the direction of x-axis and y-axis.
So the x-component of force is ${F_x} = N\sin \theta = ma$
And the y-component is ${F_y} = N\cos \theta = mg$
Dividing the x and y components :
$\dfrac{{{F_x}}}{{{F_y}}} = \dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{a}{g}$
From the above steps we get the expression for a:
$a = g\tan \theta $
So, from F=ma. We get,
$F = a\left( {M + m} \right)$
$F = g\tan \theta \left( {M + m} \right)$

Hence the correct option is (b).

Note: Use your free body diagram to identify which forces are acting in the direction of interest. Sometimes a force is completely aligned in the parallel or perpendicular direction like normal force and friction. Some forces have components in both the parallel and perpendicular direction, such as the force of gravity. In that case, the force should be broken down into the parallel and perpendicular components for substitution in the net force equations.