Question

The radius of curvature of the convex surface of a thin plano-convex lens (refractive index 1.5) is 20cm (i) Calculate the focal length of the lens. (ii) Also calculate the distance of the image of a pin placed on the axis 80cm from the lens and draw a ray diagram. (iii) Determine the magnification of the image.

(A) (a)40cm
      (b)$80c{m^2}$, on the other side of the
      (c) $+ 1$
(B) (a)50cm
      (b)$700cm$, on the other side of the
      (c) $ + 1$
(C) (a)40cm
       (b)$80cm$, on the other side of the
       (c)$ - 1$
(D) (a)$40c{m^2}$
       (b)$80cm$, on the other side of the
       (c)$ - 1$

Answer 1

Hint In Optics, magnification is simply the size of an image relative to the size of the object creating it. Magnification refers to the ratio of the length of image to the length of object measured in the plane perpendicular to the optical axis. The distance between the centre of a lens or curved mirror is known as its focal length.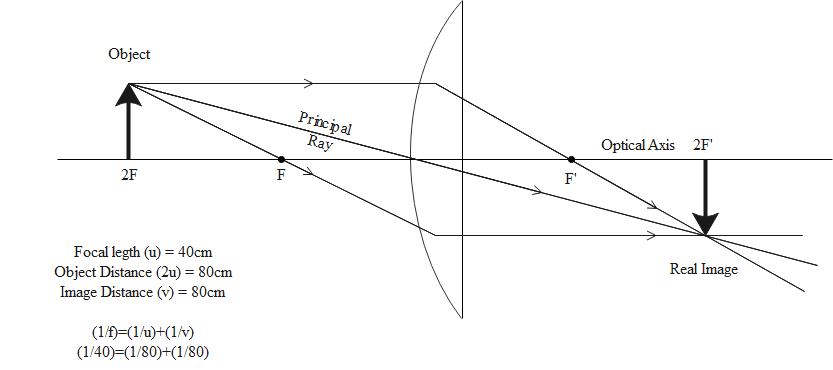



Complete step by step answer: In optics, the lens makers formula states that
$\dfrac{1}{f} = \left( {\mu - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
Where f is the focal length.
${R_1} = \infty $
${R_2} = 20cm$
Therefore, we can put the given information in the above equation and derive,
(i)$\dfrac{1}{f} = \left( {1 \cdot 5 - 1} \right)\left( {\dfrac{1}{{20}}} \right)$
Hence,
f = 40cm
(ii) Since, focal length (f) = 40cm
Let v = distance of image and let u = distance of object
Therefore,
$\dfrac{1}{u} + \dfrac{1}{v} = \dfrac{1}{f}$
$ \Rightarrow \dfrac{1}{{80}} + \dfrac{1}{v} = \dfrac{1}{{40}}$
$\Rightarrow v = 80cm$

The given diagram clearly demonstrates the solution.
(iii) Let magnification = m
$m = - \dfrac{v}{u}$
$\Rightarrow m = - \dfrac{{80}}{{80}}$
$ m = - 1$

Hence, the correct answer is Option C.

Note We must carefully understand if the lens is silvered anywhere as that would bring reflection in the question and the solution for which would completely be different. Other than that, the complexity of the question increases with involvement of more than one lens in case of which the formula used will be relative.