Question

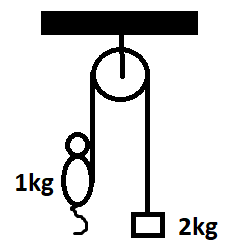
The pulley shown in the diagram is frictionless. A cat of mass 1kg moves up on the massless string so as to just lift a block of mass 2kg. After some time, the cat stops moving with respect to the string. The magnitude of the change in the cat's acceleration is:

Answer 1

Hint: In order to solve the question it is important to understand how a pulley works. If the two objects have the same weight, the pulley will not move; however, a small tug on either side will move them in one direction or the other. If the loads are different the heavier one will accelerate down while the lighter load accelerates up.

Formula Used:
The change in acceleration of any body is given by the simple mathematical formula mentioned below:
$a = {a_{initial}} - {a_{final}}$

Complete step by step answer:
According to the question, the cat is moving in an upwards direction, so initial upward acceleration of the cat will be:
${a_{initial}} = g$
Now, the final upward acceleration of the cat is given by the following mathematical expression:
${a_{final}} = \dfrac{{({m_{block}} - {m_{cat}})g}}{{({m_{block}} + {m_{cat}})}}$
Now, we know that the mass of the block is given as $2kg$ and the mass of the cat is given as $1kg$. Now, putting these values in the above equation, we obtain:
${a_{final}} = \dfrac{{(2 - 1)g}}{{(2 + 1)}} \\
\Rightarrow {a_{final}} = \dfrac{g}{3} \\ $
Now, substituting these values in the mathematical formula for calculating change in acceleration we obtain:
$ a = {a_{initial}} - {a_{final}} \\
\Rightarrow a = g - \dfrac{g}{3} = \dfrac{{2g}}{3} \\
$
Thus, we find that the change in acceleration of the cat is equal to $\dfrac{{2g}}{3}$.

Additional Information: Problems involving two objects, connecting strings and pulleys are characterized by objects that are moving (or even accelerating) in different directions. They move or accelerate at the same rate but in different directions. As such, it becomes important in approaching such problems to select a different reference frame and axes system for each object. Attention should be given to selecting an axes system such that both objects are accelerating along an axis in the positive direction. With the axes properly defined for each individual object, a free-body diagram can be constructed. Then Newton's laws can be applied to each diagram to develop a system of two equations for solving for the two unknowns.

Note: One strategy for solving two-body problems involves the use of a system analysis to determine the acceleration combined with an individual object analysis to determine the force transmitted between the objects. The second strategy involved the use of two individual object analyses in order to develop a system of two equations for solving for the two unknown quantities.