Question

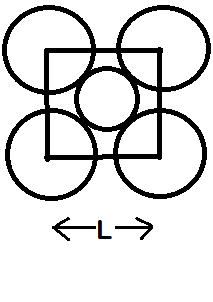
The packing efficiency of the two-dimensional square unit cell shown in the given figure is:
                                            
(A) 39.27%
(B) 68.02%
(C) 74.05%
(D) 78.54%

Answer 1

Hint: First find the total area occupied by the spheres in the unit cell and the total area of the square unit cell. Then take the ratio of area of spheres in the unit cells and the total area of the square unit cell to find the packing efficiency.

Complete step by step answer:
-Let us take the radius of each atom to be ‘r’. So, from the structure we can say that the diagonal of the square unit is ‘4r’. …….(1)
-Let the side of the square unit be ‘L’. So, the diagonal of the square will be:
  Diagonal = \[\sqrt {{L^2} + {L^2}} \] = $L\sqrt 2 $ ……...(2)
-Now since we have 2 values for the diagonal, let’s equate them to each other.
(1) = (2)
$4r = L\sqrt 2 $
$L = 4r/\sqrt 2 $ ……….(3)
-Total area (A) of the square unit can be written as:
$A = {L^2}$
In the above equation put the value of L from equation (3):
$A = {(4r/\sqrt 2 )^2}$
= $16{r^2}/2$
= $8{r^2}$ ………….(4)

-Total number of spheres inside the square unit = 1 (the one at the centre) + 4 (1/4) (from the 4 spheres at the corners, each contributing 1 / 4 to the square unit cell)
= 1 + 4 ( 1/4 ) = 2
-Area of 1 sphere = $\pi {r^2}$
Since there are 2 spheres, the total area of spheres will be = $2(\pi {r^2})$ ………...(5)
-Packing fraction or packing efficiency of the square unit cell is defined as the ratio of area occupied by the spheres and total area of the square unit cell.
Use the values of the area occupied by the sphere from equation (5) and total area of square unit cell from equation (4).
Packing efficiency = total area of spheres / total area of the square unit cell
                                 = $2(\pi {r^2})/8{r^2}$
                                = $\pi /4$ ( π = 3.14 )
                                = 0. 785
So, the percentage packing efficiency will be 78.5%.
The correct option is: (D) 78.54%

Note: The most common mistake we can make here is while calculating the contribution of the spheres (atoms) in the unit cell. So, always remember that:
-A corner atom contributes = 1 / 8 of itself to the unit cell
-A body centre atom contributes = 1
-A face centre atom contributes = 1 / 2