Question

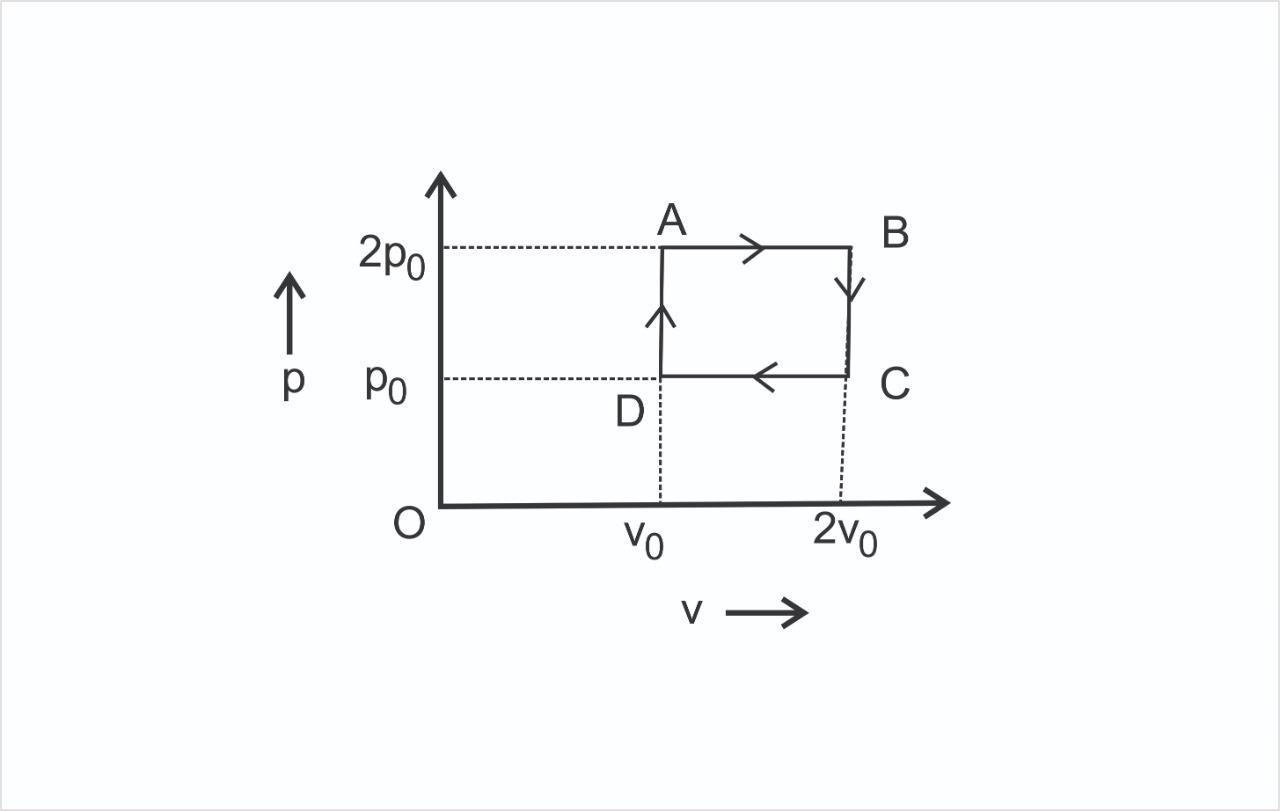
The $P - V$ diagram represents the thermodynamic cycle of an engine, operating with an ideal monatomic gas. The amount of heat extracted from the source in a single cycle is:

A) $\dfrac{{13}}{2}{P_0}{V_0}$
B) $\dfrac{{11}}{2}{P_0}{V_0}$
C) $4{P_0}{V_0}$
D) ${P_0}{V_0}$

Answer 1

Hint: In this question, Use the concept of the heat transfer that is it is a path function means it depends on the path followed by the process instead of the initial and final state. First, we discuss the various processes of this pressure vs volume diagram. Then state in which processes the heat will be extracted from the source. Calculate the heat extracted from these processes using proper formula and sign convention.

Complete step by step solution:
As we know that the cycle is a clockwise cycle. So it is a power producing cycle. The total work done in the cycle is the area of this pressure volume diagram.
We have to find the heat extracted from the source. Now heat extracted from the source will be in the $DA$ and $AB$ path.
$DA$ path is a constant volume heat addition process and $AB$ is a constant pressure expansion process.
$BC$ is a constant volume heat rejection process. $CD$ is a constant pressure contraction process.
So, we will get the total heat extracted is,
${Q_{Total}} = {Q_{DA}} + {Q_{AB}}$
$ \Rightarrow {Q_{total}} = n{C_V}dT + n{C_P}dT$
Here, the number of moles is $n$, the molar specific heat at constant volume and pressure are ${C_p}$ and ${C_V}$. As we know that, ${C_p} = \dfrac{{3R}}{2}$ and ${C_V} = \dfrac{{5R}}{2}$, where, $R$ is the universal gas constant.
Now, the heat transfer equation become,
$ \Rightarrow {Q_{total}} = n{C_V}\left( {2{T_0} - {T_0}} \right) + n{C_P}\left( {4{T_0} - {T_0}} \right)$
$ \Rightarrow {Q_{total}} = n{C_V}{T_0} + 3n{C_P}{T_0}$
Now, we substitute the value of ${C_P}$ and ${C_V}$ then we get
${Q_{total}} = \dfrac{{n3R{T_0}}}{2} + \dfrac{{n5R(2{T_0})}}{2}$
$ \Rightarrow {Q_{total}} = \dfrac{{13}}{2}nR{T_0}$
As we know from the ideal gas equation ${P_0}{V_0} = nR{T_0}$, so the equation become,
$ \Rightarrow {Q_{total}} = \dfrac{{13}}{2}{P_0}{V_0}$
Hence, the amount of heat extracted from the source in a single cycle is ${Q_{total}} = \dfrac{{13}}{2}{P_0}{V_0}$.

Thus, the correct Option is (A).

Note: Here, we have to follow the sign convention of heat addition and heat rejection that is when heat is added to the system it is taken as positive and when heat is rejected from the system it is taken negative.