Question

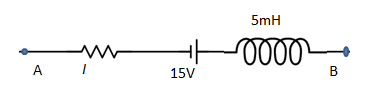
The network shown in the figure is a part of a complete circuit. If at a certain instant , the current I is $5\,A$ and it is decreasing at a rate of ${10^3}\,A{s^{ - 1}}$ then ${V_A} - {V_B}$ equals:


A) $20\,V$
B) $15\,V$
C) $10\,V$
D) $5\,V$

Answer 1

Hint: We know that electric potential depends on the location therefore; starting from any point if we come to the same point back the total change in potential must be zero.
Finally we get the required answer.

Complete step by step answer:
Kirchhoff’s second rule, stated as the algebraic sum of changes in potential around any loop involving cells and resistors in the loop, is zero.
We know that voltage drop along inductor is
$e = - L\dfrac{{dI}}{{dt}}$
The circuit shown in the figure involves an inductor as well as a resistor so while applying Kirchhoff’s law we can consider potential drop across both inductor and resistor.
By applying Kirchhoff’s rule in the given part of the circuit from moving A to B we get
${V_A} - IR + E - L\dfrac{{dI}}{{dt}} = {V_B}$
It is given that
Current $(I) = 5\,A$
Resistance $\left( R \right) = 1\Omega $
Inductance$\left( L \right) = 5\,mH$
Rate of decrease current means $\dfrac{{dI}}{{dt}} = \, - {10^{ - 3\,}}A{s^{ - 1}}$
A negative sign occurs because the current is decreasing
EMF$\left( E \right) = 15\,V$
Now by putting the values of $I,R,L\,and\,\dfrac{{dI}}{{dt}}$ in the equation we get
${V_A} - 5 \times 1 + 15 - 5 \times {10^{ - 3}} \times \left( { - {{10}^{ - 3}}} \right) = {V_B}$
${V_B} - {V_A} = 15$

Hence the correct option is (B) $15\,V$

Note: Kirchhoff’s gave two rules for analysing electric current
Kirchhoff’s first rule- According to this rule, the total amount of charge or current entering each junction is equal to the amount of current leaving the junction at that point. The first law of Kirchhoff’s is also known by the name of junction rule. This law works on the principle of conservation of charge.
Kirchhoff’s second rule states that the algebraic sum of changes in potential around any loop involving resistors and cells in the loop is zero. The second law of Kirchhoff is also known by the name of the loop rule. This law is based on conservation of energy.
While the solution keeps in mind the negative sign of the rate of Change of current.