Question

The locus of the foot of the perpendicular from the origin on each member of the family \[(4a+3)x-(a+1)y-(2a+1)=0\] is
(a). \[{{(2x-1)}^{2}}+4{{(y+1)}^{2}}=5\]
(b). \[{{(2x-1)}^{2}}+{{(y+1)}^{2}}=5\]
(c). \[{{(2x+1)}^{2}}+4{{(y-1)}^{2}}=5\]
(d). \[{{(2x-1)}^{2}}+4{{(y-1)}^{2}}=5\]

Answer 1

Hint:- In this question first we have to find the value of the point of intersection of the family of straight lines then apply Pythagoras theorem to get the required answer.

Complete step-by-step solution -
The equation of the family of lines is,
\[(4a+3)x-(a+1)y-(2a+1)=0\]
Expanding this, we get
\[4ax+3x-ay-y-2a-1=0\]
Now regrouping them, we get
\[3x-y-1+a(4x-y-2)=0\]
Now this is of the form \[{{L}_{1}}+\lambda {{L}_{2}}=0\].
Let the point of intersection of these two lines, i.e., \[3x-y-1=0\]and \[4x-y-2=0\]be P.
So, the given family of lines will pass through this fixed point P, as shown below.

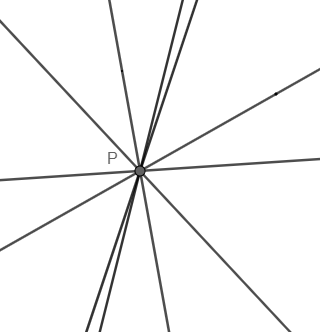
Now we will find the coordinates of point P.
Consider,
\[3x-y-1=0\]
\[3x=y+1\]
\[x=\dfrac{y+1}{3}........(i)\]
Substitute this value in other equation of line, we get
\[4x-y-2=0\]
\[4\left( \dfrac{y+1}{3} \right)-y-2=0\]
\[\dfrac{4y+4-3y-(3\times 2)}{3}=0\]
\[y+4-6=0\]
\[y=6-4=2\]
Substituting the value of ‘y’ in equation (i), we get
\[x=\dfrac{2+1}{3}=\dfrac{3}{3}=1\]
So, the point of intersection of the family of lines is \[P(1,2)\].
Now, there is a perpendicular drawn from the origin onto each line. Let the foot of the perpendicular on each line be \[A(x,y)\], as shown below.

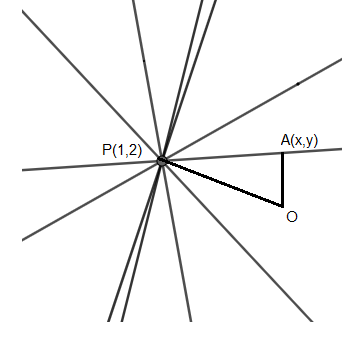
Now the points OPA will form a right-angled triangle in all the lines.
Applying Pythagoras theorem on \[\Delta OPA\], we get
\[O{{P}^{2}}=O{{A}^{2}}+A{{P}^{2}}.........(ii)\]
We know the distance between points \[({{x}_{1}},{{y}_{1}})\]and \[({{x}_{2}},{{y}_{2}})\]is given by the distance formula, i.e.,
\[\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}\]
Applying the distance formula in equation (ii), we get
\[{{\left( \sqrt{{{(1-0)}^{2}}+{{(2-0)}^{2}}} \right)}^{2}}={{\left( \sqrt{{{(x-0)}^{2}}+{{(y-0)}^{2}}} \right)}^{2}}+{{\left( \sqrt{{{(x-1)}^{2}}+{{(y-2)}^{2}}} \right)}^{2}}\]
\[{{1}^{2}}+{{2}^{2}}={{x}^{2}}+{{y}^{2}}+{{(x-1)}^{2}}+{{(y-2)}^{2}}\]
Expanding, we get
\[1+4={{x}^{2}}+{{y}^{2}}+({{x}^{2}}+1-2x)+({{y}^{2}}+4-4y)\]
\[5=2{{x}^{2}}+2{{y}^{2}}+1-2x+4-4y\]
As this is not matching with the options, we will multiply the above equation with \[2\], we get
\[10=4{{x}^{2}}+4{{y}^{2}}+2-4x+8-8y\]
Grouping them, we get
\[4{{x}^{2}}-4x+2+4{{y}^{2}}-8y+8=10\]
Now we will try to convert this into \[{{(a+b)}^{2}}\]form, as in options.
\[\left( 4{{x}^{2}}-4x+1 \right)+1+4({{y}^{2}}-2y+1)+4=10\]
We know, \[\left( {{a}^{2}}-2ab+{{b}^{2}} \right)={{(a+b)}^{2}}\], so above equation can be re-written as,
\[{{\left( 2x-1 \right)}^{2}}+4{{(y-1)}^{2}}=10-4-1\]
\[{{\left( 2x-1 \right)}^{2}}+4{{(y-1)}^{2}}=5\]
So, the locus of the foot of the perpendicular from the origin on each member of the family \[(4a+3)x-(a+1)y-(2a+1)=0\] is \[{{\left( 2x-1 \right)}^{2}}+4{{(y-1)}^{2}}=5\].
Hence, the correct answer is option (d).

Note: Another method to find the answer is, instead of using Pythagoras theorem; we can find the slope of the equation of perpendicular line from the origin to a point. Then applying the formula, $y=mx+c$. But this would be a lengthy process.