
The equations of the straight lines are \[x + y = 0\], \[5x + y = 4\] and \[x + 5y = 4\]. Then what is the type of a triangle formed by these lines?
A. an isosceles triangle
B. an equilateral triangle
C. a scalene triangle
D. a right-angled triangle
Answer
219.6k+ views
Hint: In the given question, three equations of the straight lines are given. By solving the equations, we will find the points of intersections of the lines. Then by using the distance formula, we will find the distance between two vertices of the formed triangle.
Formula Used:
The distance between the two points \[A\left( {{x_1},{y_1}} \right)\] and \[B\left( {{x_2},{y_2}} \right)\] is:
\[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \]
Complete step by step solution:
The given equations of straight lines are:
\[x + y = 0\] …….(1)
\[5x + y = 4\] …….(2)
\[x + 5y = 4\] …….(3)
Let’s solve the equations and find the points of intersections of the lines.
Rewrite equation in term \[y\].
\[y = - x\] …..(4)
Now solve the equations (4) and (2).
Substitute \[x = - y\] in equation (2).
\[5\left( { - y} \right) + y = 4\]
\[ \Rightarrow \]\[ - 4y = 4\]
\[ \Rightarrow \]\[y = - 1\]
Then, \[x = 1\].
The point of intersection of \[x + y = 0\] and \[5x + y = 4\] is \[\left( {1, - 1} \right)\].
Now solve the equations (4) and (3).
Substitute \[x = - y\] in equation (3).
\[ - y + 5y = 4\]
\[ \Rightarrow \]\[4y = 4\]
\[ \Rightarrow \]\[y = 1\]
Then, \[x = - 1\].
The point of intersection of \[x + y = 0\] and \[x + 5y = 4\] is \[\left( { - 1,1} \right)\].
Now solve the equations (2) and (3).
Substitute \[x = 4 - 5y\] in equation (2).
\[5\left( {4 - 5y} \right) + y = 4\]
\[ \Rightarrow \]\[20 - 25y + y = 4\]
\[ \Rightarrow \]\[ - 24y = - 16\]
\[ \Rightarrow \]\[y = \dfrac{2}{3}\]
Then, \[x = \dfrac{2}{3}\].
The point of intersection of \[5x + y = 4\] and \[x + 5y = 4\] is \[\left( {\dfrac{2}{3},\dfrac{2}{3}} \right)\].
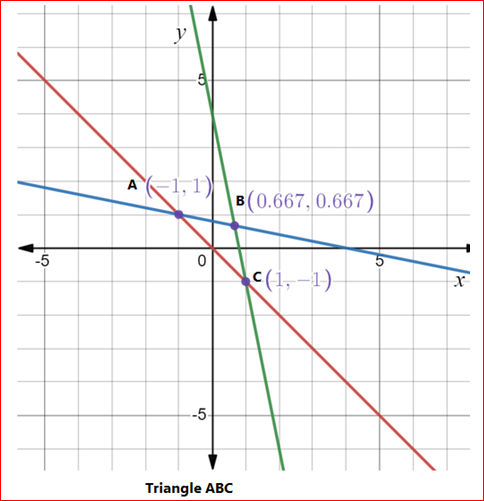
Now apply distance formula to calculate the distance between the two vertices \[A\left( { - 1,1} \right)\] and \[B\left( {\dfrac{2}{3},\dfrac{2}{3}} \right)\].
\[AB = \sqrt {{{\left( {\dfrac{2}{3} + 1} \right)}^2} + {{\left( {\dfrac{2}{3} - 1} \right)}^2}} \]
\[ \Rightarrow \]\[AB = \sqrt {{{\left( {\dfrac{5}{3}} \right)}^2} + {{\left( {\dfrac{{ - 1}}{3}} \right)}^2}} \]
\[ \Rightarrow \]\[AB = \sqrt {\dfrac{{26}}{9}} \]
Now apply distance formula to calculate the distance between the two vertices \[A\left( { - 1,1} \right)\] and \[C\left( {1, - 1} \right)\].
\[AC = \sqrt {{{\left( {1 + 1} \right)}^2} + {{\left( { - 1 - 1} \right)}^2}} \]
\[ \Rightarrow \]\[AC = \sqrt {{{\left( 2 \right)}^2} + {{\left( 2 \right)}^2}} \]
\[ \Rightarrow \]\[AC = \sqrt 8 \]
\[ \Rightarrow \]\[AC = 2\sqrt 2 \]
Now apply distance formula to calculate the distance between the two vertices \[B\left( {\dfrac{2}{3},\dfrac{2}{3}} \right)\] and \[C\left( {1, - 1} \right)\].
\[BC = \sqrt {{{\left( {\dfrac{2}{3} - 1} \right)}^2} + {{\left( {\dfrac{2}{3} + 1} \right)}^2}} \]
\[ \Rightarrow \]\[BC = \sqrt {{{\left( {\dfrac{{ - 1}}{3}} \right)}^2} + {{\left( {\dfrac{5}{3}} \right)}^2}} \]
\[ \Rightarrow \]\[BC = \sqrt {\dfrac{{26}}{9}} \]
Since, the length of two sides of a triangle is equal. i.e., \[AB = BC\].
So, the triangle formed by the lines is an isosceles triangle.
Hence the correct option is A.
Note: Students are often confused with the formula \[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \] and \[d = \sqrt {{{\left( {{x_2} + {x_1}} \right)}^2} - {{\left( {{y_2} + {y_1}} \right)}^2}} \] . But the correct distance formula is \[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \].
Formula Used:
The distance between the two points \[A\left( {{x_1},{y_1}} \right)\] and \[B\left( {{x_2},{y_2}} \right)\] is:
\[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \]
Complete step by step solution:
The given equations of straight lines are:
\[x + y = 0\] …….(1)
\[5x + y = 4\] …….(2)
\[x + 5y = 4\] …….(3)
Let’s solve the equations and find the points of intersections of the lines.
Rewrite equation in term \[y\].
\[y = - x\] …..(4)
Now solve the equations (4) and (2).
Substitute \[x = - y\] in equation (2).
\[5\left( { - y} \right) + y = 4\]
\[ \Rightarrow \]\[ - 4y = 4\]
\[ \Rightarrow \]\[y = - 1\]
Then, \[x = 1\].
The point of intersection of \[x + y = 0\] and \[5x + y = 4\] is \[\left( {1, - 1} \right)\].
Now solve the equations (4) and (3).
Substitute \[x = - y\] in equation (3).
\[ - y + 5y = 4\]
\[ \Rightarrow \]\[4y = 4\]
\[ \Rightarrow \]\[y = 1\]
Then, \[x = - 1\].
The point of intersection of \[x + y = 0\] and \[x + 5y = 4\] is \[\left( { - 1,1} \right)\].
Now solve the equations (2) and (3).
Substitute \[x = 4 - 5y\] in equation (2).
\[5\left( {4 - 5y} \right) + y = 4\]
\[ \Rightarrow \]\[20 - 25y + y = 4\]
\[ \Rightarrow \]\[ - 24y = - 16\]
\[ \Rightarrow \]\[y = \dfrac{2}{3}\]
Then, \[x = \dfrac{2}{3}\].
The point of intersection of \[5x + y = 4\] and \[x + 5y = 4\] is \[\left( {\dfrac{2}{3},\dfrac{2}{3}} \right)\].

Now apply distance formula to calculate the distance between the two vertices \[A\left( { - 1,1} \right)\] and \[B\left( {\dfrac{2}{3},\dfrac{2}{3}} \right)\].
\[AB = \sqrt {{{\left( {\dfrac{2}{3} + 1} \right)}^2} + {{\left( {\dfrac{2}{3} - 1} \right)}^2}} \]
\[ \Rightarrow \]\[AB = \sqrt {{{\left( {\dfrac{5}{3}} \right)}^2} + {{\left( {\dfrac{{ - 1}}{3}} \right)}^2}} \]
\[ \Rightarrow \]\[AB = \sqrt {\dfrac{{26}}{9}} \]
Now apply distance formula to calculate the distance between the two vertices \[A\left( { - 1,1} \right)\] and \[C\left( {1, - 1} \right)\].
\[AC = \sqrt {{{\left( {1 + 1} \right)}^2} + {{\left( { - 1 - 1} \right)}^2}} \]
\[ \Rightarrow \]\[AC = \sqrt {{{\left( 2 \right)}^2} + {{\left( 2 \right)}^2}} \]
\[ \Rightarrow \]\[AC = \sqrt 8 \]
\[ \Rightarrow \]\[AC = 2\sqrt 2 \]
Now apply distance formula to calculate the distance between the two vertices \[B\left( {\dfrac{2}{3},\dfrac{2}{3}} \right)\] and \[C\left( {1, - 1} \right)\].
\[BC = \sqrt {{{\left( {\dfrac{2}{3} - 1} \right)}^2} + {{\left( {\dfrac{2}{3} + 1} \right)}^2}} \]
\[ \Rightarrow \]\[BC = \sqrt {{{\left( {\dfrac{{ - 1}}{3}} \right)}^2} + {{\left( {\dfrac{5}{3}} \right)}^2}} \]
\[ \Rightarrow \]\[BC = \sqrt {\dfrac{{26}}{9}} \]
Since, the length of two sides of a triangle is equal. i.e., \[AB = BC\].
So, the triangle formed by the lines is an isosceles triangle.
Hence the correct option is A.
Note: Students are often confused with the formula \[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \] and \[d = \sqrt {{{\left( {{x_2} + {x_1}} \right)}^2} - {{\left( {{y_2} + {y_1}} \right)}^2}} \] . But the correct distance formula is \[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \].
Recently Updated Pages
Geometry of Complex Numbers Explained

Electricity and Magnetism Explained: Key Concepts & Applications

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

JEE Main 2021 July 25 Shift 1 Question Paper with Answer Key

JEE Main 2021 July 22 Shift 2 Question Paper with Answer Key

Trending doubts
Understanding Atomic Structure for Beginners

Understanding Centrifugal Force in Physics

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Average and RMS Value in Electrical Circuits

Understanding Entropy Changes in Different Processes

Other Pages
NCERT Solutions for Class 11 Maths Chapter 6 Permutations And Combinations

Common Ion Effect: Concept, Applications, and Problem-Solving

Understanding Excess Pressure Inside a Liquid Drop

NCERT Solutions for Class 11 Maths Chapter 7 Permutations and Combinations

Understanding Elastic Collisions in Two Dimensions

Devuthani Ekadashi 2025: Correct Date, Shubh Muhurat, Parana Time & Puja Vidhi




