
The differential equation of all circles which passes through the origin and whose center lie on \[y\]-axis, is
A. \[\left( {{x^2} - {y^2}} \right)\frac{{dy}}{{dx}} - 2xy = 0\]
B. \[\left( {{x^2} - {y^2}} \right)\frac{{dy}}{{dx}} + 2xy = 0\]
C. \[\left( {{x^2} - {y^2}} \right)\frac{{dy}}{{dx}} - xy = 0\]
D. \[\left( {{x^2} - {y^2}} \right)\frac{{dy}}{{dx}} + xy = 0\]
Answer
218.1k+ views
HINT:
In order to obtain the circle's resulting equation, we employ the assumption that the circle passes through the origin and only touches the\[y\]-axis there to begin the problem-solving process. Then, in order to determine the values of any arbitrary constants included in the equation, we begin differentiating the acquired equation of circles on both sides with respect to\[y\]. In order to reach the desired result, we then substitute this calculated value for the arbitrary constant into the equation of circles and do the appropriate calculations.
Formula use:
\[y = {x^n}\]
Differentiate with respect to x
\[\frac{{dy}}{{dx}} = n{x^{n-1}}\]
Complete step-by-step solution:
The issue requires us to identify every circle's differential equation that touches the y-axis at the origin.
Let's start by determining the equation of the circle at the origin that touches the x-axis.
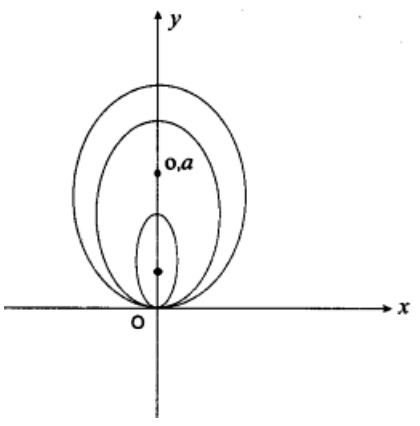
The circles pass through the origin, they have their centers at \[\left( {0,a} \right)\]
The circles have radius.
So, the equation of the family of circles in given by
\[{x^2} + {(y - a)^2} = {a^2}\]
In the above equation, ‘a’ is said to be any arbitrary constant.
\[{x^2} + {y^2} - 2ay + {a^2} = {a^2}\]
\[{x^2} + {y^2} = 2ay \ldots \ldots .(1)\]
As the above equation has only one arbitrary constant, we can obtain first order differential equation:
Differentiating the equation (1) with respect to x
\[2x + 2y\frac{{dy}}{{dx}} = 2a\frac{{dy}}{{dx}}\]
\[ \Rightarrow a = \frac{{x + y\frac{{dy}}{{dx}}}}{{\frac{{dy}}{{dx}}}} \ldots \ldots \ldots \ldots (2)\]
Substituting the value of \[{\rm{a}}\] in equation\[{\rm{2}}\]we get:
\[{x^2} + {\left( {y - y - \frac{x}{{\frac{{dy}}{{dx}}}}} \right)^2} = {\left( {y + \frac{x}{{\frac{{dy}}{{dx}}}}} \right)^2}\]
Solve the square root for the above equation:
\[ \Rightarrow {x^2} + \frac{{{x^2}}}{{{{\left( {\frac{{dy}}{{dx}}} \right)}^2}}} = {y^2} + 2\frac{{xy}}{{\frac{{dy}}{{dx}}}} + \frac{{{x^2}}}{{{{\left( {\frac{{dy}}{{dx}}} \right)}^2}}}\]
Simplify the above equation to make it less complicated:
\[ \Rightarrow {x^2} = {y^2} + 2\frac{{xy}}{{\frac{{dy}}{{dx}}}}\]
Let's restructure the equation above to specifically get \[2xy\] on one side. The result is as follows:
\[ \Rightarrow \left( {{x^2} - {y^2}} \right)\frac{{dy}}{{dx}} = 2xy\]
Therefore, \[\left( {{x^2} - {y^2}} \right)\frac{{dy}}{{dx}} = 2xy\] is the required differential equation of all circles which passes through the origin and whose center lie on \[y\]-axis.
Hence, the option A is correct.
Note:
We should be aware that the centers of all circles touching the x-axis at the origin will be on the y-axis. Given that it reflects the equations of all the circles matching the specified criteria, q is known as an arbitrary constant. We differentiate the equation 'n' times to obtain the values of all arbitrary constants if the equation has 'n' arbitrary constants. Finding the differential equation of the circles that intersect the y-axis at the origin will also likely present challenges.
In order to obtain the circle's resulting equation, we employ the assumption that the circle passes through the origin and only touches the\[y\]-axis there to begin the problem-solving process. Then, in order to determine the values of any arbitrary constants included in the equation, we begin differentiating the acquired equation of circles on both sides with respect to\[y\]. In order to reach the desired result, we then substitute this calculated value for the arbitrary constant into the equation of circles and do the appropriate calculations.
Formula use:
\[y = {x^n}\]
Differentiate with respect to x
\[\frac{{dy}}{{dx}} = n{x^{n-1}}\]
Complete step-by-step solution:
The issue requires us to identify every circle's differential equation that touches the y-axis at the origin.
Let's start by determining the equation of the circle at the origin that touches the x-axis.

The circles pass through the origin, they have their centers at \[\left( {0,a} \right)\]
The circles have radius.
So, the equation of the family of circles in given by
\[{x^2} + {(y - a)^2} = {a^2}\]
In the above equation, ‘a’ is said to be any arbitrary constant.
\[{x^2} + {y^2} - 2ay + {a^2} = {a^2}\]
\[{x^2} + {y^2} = 2ay \ldots \ldots .(1)\]
As the above equation has only one arbitrary constant, we can obtain first order differential equation:
Differentiating the equation (1) with respect to x
\[2x + 2y\frac{{dy}}{{dx}} = 2a\frac{{dy}}{{dx}}\]
\[ \Rightarrow a = \frac{{x + y\frac{{dy}}{{dx}}}}{{\frac{{dy}}{{dx}}}} \ldots \ldots \ldots \ldots (2)\]
Substituting the value of \[{\rm{a}}\] in equation\[{\rm{2}}\]we get:
\[{x^2} + {\left( {y - y - \frac{x}{{\frac{{dy}}{{dx}}}}} \right)^2} = {\left( {y + \frac{x}{{\frac{{dy}}{{dx}}}}} \right)^2}\]
Solve the square root for the above equation:
\[ \Rightarrow {x^2} + \frac{{{x^2}}}{{{{\left( {\frac{{dy}}{{dx}}} \right)}^2}}} = {y^2} + 2\frac{{xy}}{{\frac{{dy}}{{dx}}}} + \frac{{{x^2}}}{{{{\left( {\frac{{dy}}{{dx}}} \right)}^2}}}\]
Simplify the above equation to make it less complicated:
\[ \Rightarrow {x^2} = {y^2} + 2\frac{{xy}}{{\frac{{dy}}{{dx}}}}\]
Let's restructure the equation above to specifically get \[2xy\] on one side. The result is as follows:
\[ \Rightarrow \left( {{x^2} - {y^2}} \right)\frac{{dy}}{{dx}} = 2xy\]
Therefore, \[\left( {{x^2} - {y^2}} \right)\frac{{dy}}{{dx}} = 2xy\] is the required differential equation of all circles which passes through the origin and whose center lie on \[y\]-axis.
Hence, the option A is correct.
Note:
We should be aware that the centers of all circles touching the x-axis at the origin will be on the y-axis. Given that it reflects the equations of all the circles matching the specified criteria, q is known as an arbitrary constant. We differentiate the equation 'n' times to obtain the values of all arbitrary constants if the equation has 'n' arbitrary constants. Finding the differential equation of the circles that intersect the y-axis at the origin will also likely present challenges.
Recently Updated Pages
Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE General Topics in Chemistry Important Concepts and Tips

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

Algebra Made Easy: Step-by-Step Guide for Students

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Understanding Atomic Structure for Beginners

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections

NCERT Solutions for Class 11 Maths Chapter 9 Straight Lines

NCERT Solutions For Class 11 Maths Chapter 8 Sequences And Series

How to Convert a Galvanometer into an Ammeter or Voltmeter

NCERT Solutions For Class 11 Maths Chapter 12 Limits And Derivatives




