Question

The complex numbers \[{{z}_{1}},{{z}_{2}},{{z}_{3}}\] are the vertices of a triangle. Then the complex numbers \[z\] which make the triangle into a parallelogram is
A. \[{{z}_{1}}+{{z}_{2}}-{{z}_{3}}\]
B. \[{{z}_{1}}-{{z}_{2}}+{{z}_{3}}\]
C. \[{{z}_{2}}+{{z}_{3}}-{{z}_{1}}\]
D. All of the above

Answer 1

Hint: In this question, we have to find the condition that makes the triangle into a parallelogram. For this, the complex vertices are used. Since we know that the opposite sides of a parallelogram are parallel and are equal in length, then we can frame the condition for the given triangle to form a parallelogram.

Formula Used: The complex number $(x,y)$ is represented by $x+iy$.
If $z=x+iy\in C$, then $x$ is called the real part and $y$ is called the imaginary part of $z$. These are represented by $\operatorname{Re}(z)$ and $\operatorname{Im}(z)$ respectively.
$z=x+iy$ be a complex number such that $\left| z \right|=r$ and $\theta $ be the amplitude of $z$. So, $\cos \theta =\dfrac{x}{r},\sin \theta =\dfrac{b}{r}$
And we can write the magnitude as
 $\begin{align}
  & \left| z \right|=\left| x+iy \right| \\
 & \Rightarrow r=\sqrt{{{x}^{2}}+{{y}^{2}}} \\
\end{align}$
Thus, we can write
$z=x+iy=r\cos \theta +ir\sin \theta =r(\cos \theta +i\sin \theta )$
This is said to be the mod amplitude form or the polar form of $z$.
Where $\cos \theta +i\sin \theta $ is denoted by $cis\theta $ and the Euler’s formula is $\cos \theta +i\sin \theta ={{e}^{i\theta }}$

Complete step by step solution: Given that,
The vertices of a triangle are represented by the complex numbers \[{{z}_{1}},{{z}_{2}},{{z}_{3}}\].
So, consider those vertices as $A({{z}_{1}}),B({{z}_{2}}),C({{z}_{3}})$
Consider point $P$ that is represented by the complex number \[z\].
Then, we can construct three parallelograms from the triangle by adding the point $P$ as fourth vertices. Shown in the diagram below:

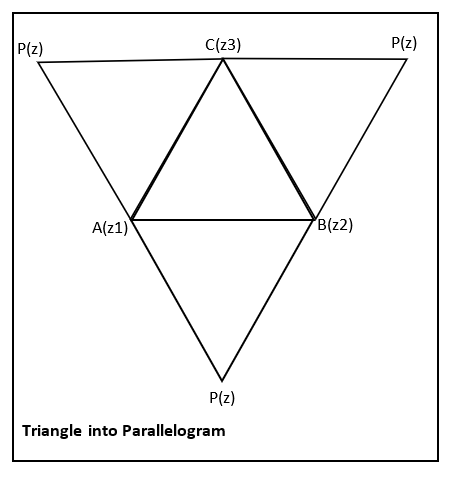
The three parallelograms we can construct are:
\[\begin{array}{*{35}{l}}
   1)\text{ }A,B,P,C \\
   2)B,P,C,A \\
   3)C,A,P,B \\
\end{array}\]
In the first case, the vertices$A,B,P,C$ to form a parallelogram there must be $\overrightarrow{AB}=\overrightarrow{CP}$.
Then,
\[\begin{align}
  & \overrightarrow{AB}=\overrightarrow{CP} \\
 & \Rightarrow ({{z}_{2}}-{{z}_{1}})=(z-{{z}_{3}}) \\
 & \Rightarrow z={{z}_{2}}+{{z}_{3}}-{{z}_{1}}\text{ }...(1) \\
\end{align}\]
In the second case, the vertices \[B,P,C,A\]to form a parallelogram there must be $\overrightarrow{BC}=\overrightarrow{AP}$.
Then,
\[\begin{align}
  & \overrightarrow{BC}=\overrightarrow{AP} \\
 & \Rightarrow ({{z}_{3}}-{{z}_{2}})=(z-{{z}_{1}}) \\
 & \Rightarrow z={{z}_{1}}+{{z}_{3}}-{{z}_{2}}\text{ }...(2) \\
\end{align}\]
In the third case, the vertices \[C,A,P,B\]to form a parallelogram there must be $\overrightarrow{CA}=\overrightarrow{BP}$.
Then,
\[\begin{align}
  & \overrightarrow{CA}=\overrightarrow{BP} \\
 & \Rightarrow ({{z}_{1}}-{{z}_{3}})=(z-{{z}_{2}}) \\
 & \Rightarrow z={{z}_{1}}+{{z}_{2}}-{{z}_{3}}\text{ }...(3) \\
\end{align}\]
Thus, all these three conditions lead the given triangle to form into a parallelogram.

Option ‘D’ is correct

Note: Here we need to remember the property of a parallelogram, that is the opposite vertices of a triangle are parallel to each other and are equal in their lengths.